2.5.2 Условия теплового подобия.

Тепловое подобие заключается в подобии температурных полей и тепловых потоков. При этом это полагается предварительное обязательное геометрическое и гидромеханическое подобия.

Для ввода критериальных чисел теплового подобия воспользуемся уравнением теплообмена и энергии. Для простоты уравнения энергии рассмотрим для одномерного нестационарного случая (сокращение записи).

Пусть имеем две подобные системы. Запишем для них уравнение теплообмена и энергии:

1-ая система 2-ая система

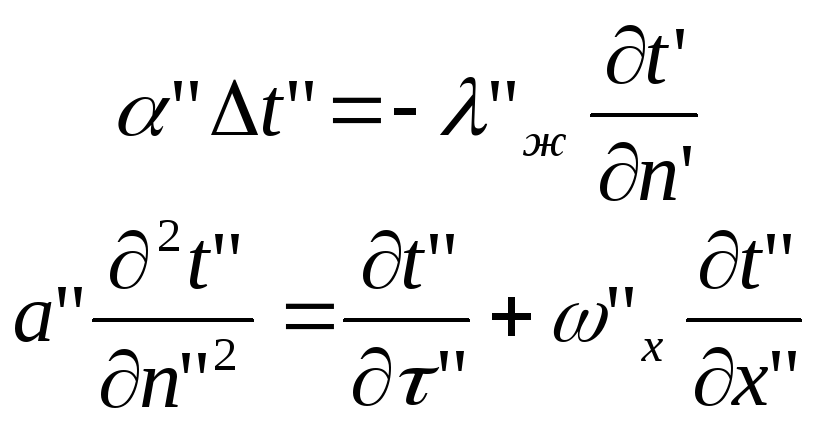(1) (2)

Так как процессы подобны, то для них отношения сходства величин постоянны и равны соответствующим константам подобия

;;;;;;(*)

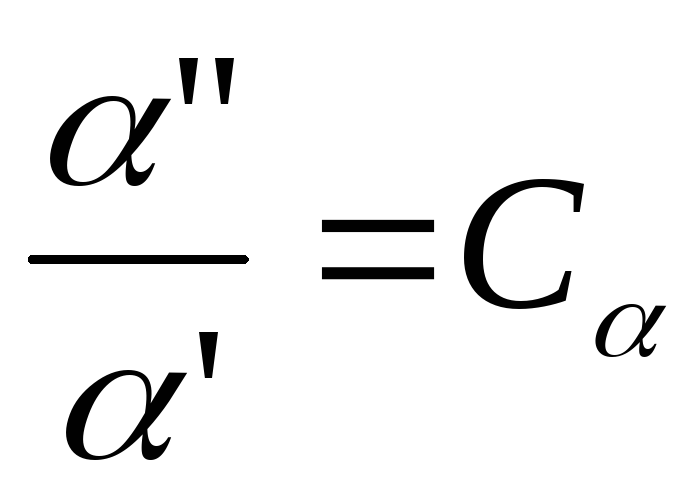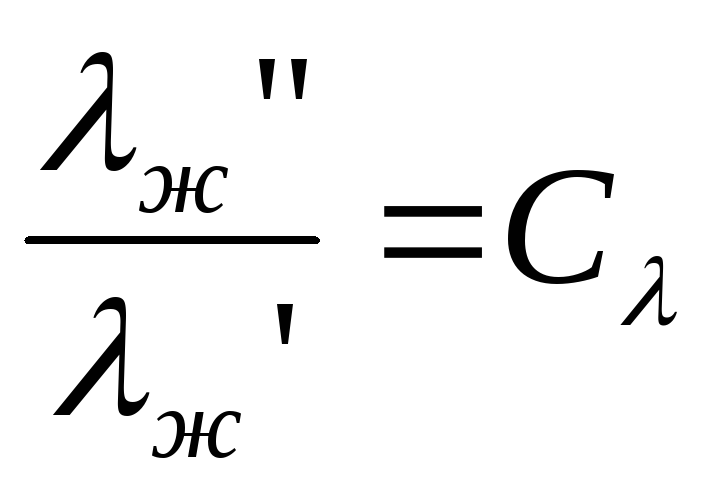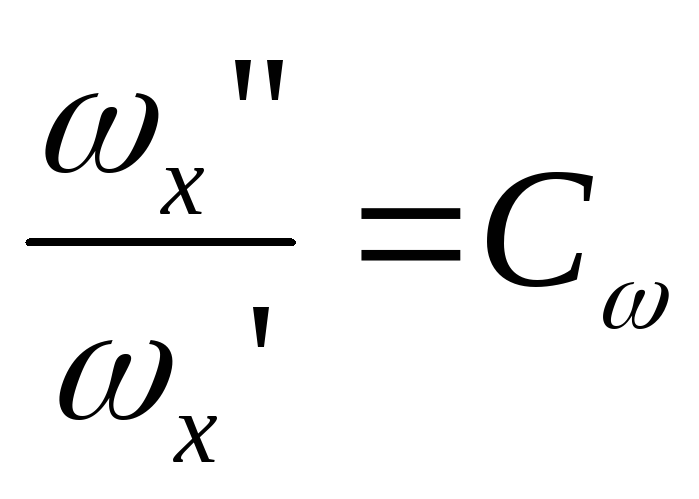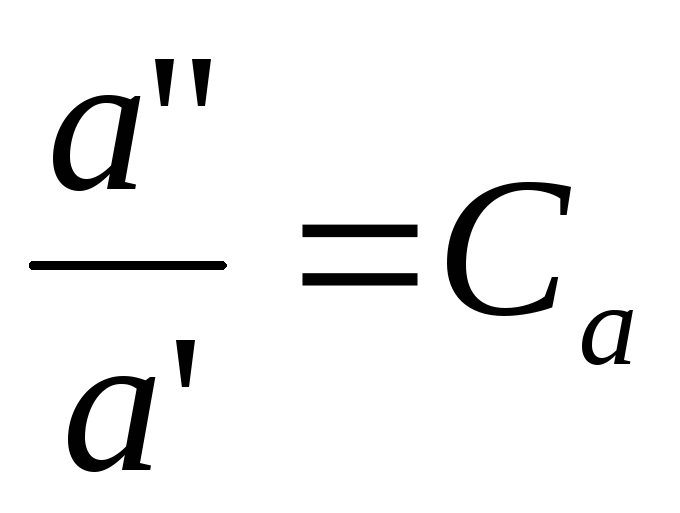Выразим, как и в случае вывода чисел гидромеханического подобия, все переменные в уравнении (2) через переменные уравнений (1) с помощью соотношений (*). Я буду выражать и сразу группировать, что бы было меньше писанины.

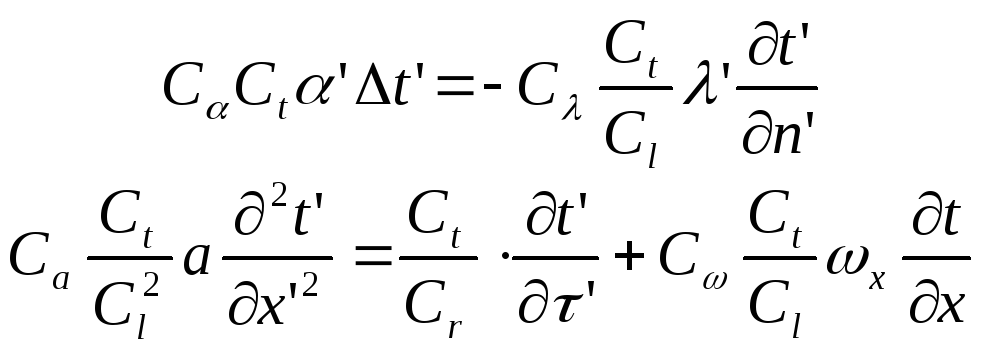(3)

Мы видим, что уравнение (1) и (3) состоит из одинаковых переменных. Которые должны из них определяться одинаково. Поэтому в уравнениях (3) должны сокращаться безразмерные комплексы состоящие из констант подобия.

Итак мы получим соотношения между константами теплового подобия. Рассматривая эти комплексы попарно можно получить числа теплового подобия.

Из условия:, для получения из полученного индикатора подобия числа теплового подобия подставим в него значения констант подобия из уравнений (*)

;;

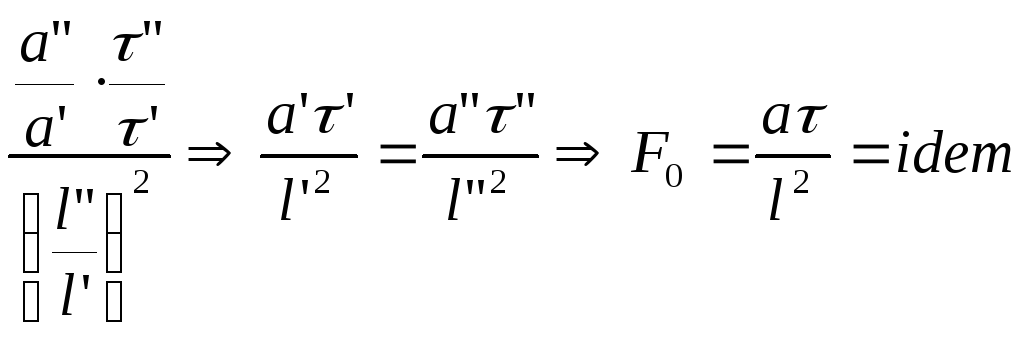
F₀ – число Фурье – оно характеризует не стационарность тепловых процессов и выражает соотношение между скоростью изменения температурного поля, размерами и физическими свойствами тела. Чем выше F₀ – тем скорее греется тело.

Из условия: и по аналогии с предыдущим получим критериальное число подобия.

или учитывается, что ;;;

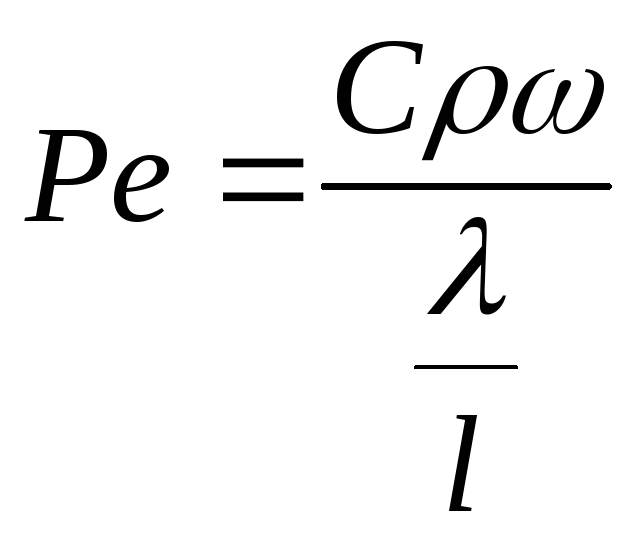
Pe – число Пекле – оно характеризует соотношение между переносом теплоты конвекцией и теплопроводностью в потоке жидкости. Т.е. можно сказать, что число Пекле характеризует подобие температурных полей.

Если в изучаемых системах температурное поле подобны, то для них

Из условия: и далее получим критериальное число подобия

;;;

Nu – число Нуссельта – оно характеризует интенсивность теплообмена на границе раздела жидкости и твердого тела, т. е. интенсивность теплоотдачи. Это безразмерный коэффициент теплоотдачи. Число Нуссельта является определяемым, т.к. в его состав входит искомый коэффициент теплоотдачи “”

Теперь мы можем сформулировать и условия теплового подобия.

При тепловом подобии систем в любых сходственных точках и сходственные моменты времени числа подобия Fo, Pe и Nu должны иметь одинаковые значения:

Nu=f(F₀;Pe)

Введем еще одно важное число подобия. Если мы с вами посмотрим на числа и , то уведем, что у них одинаковые числители. В знаменателе Re - - кинематическая вязкость от которой зависит характер скоростей. А в Pe – a - коэффициент температуропроводности - от нее зависит темп изменения температурного поля.

;

Pr – число Прандтля – оно состоит только из физических свойств жидкости и само является физическим свойством. Зависит только от рода жидкости и её состояния. Оно представляет собой соотношение между гидродинамическим и тепловым пограничными слоями.

Для идеальных газов Pr – от 0,66 – 1 не зависит от температуры и давления. Для жидкостей Pr больше 1 и является функцией температуры. Для жидких металлов Pr много меньше 1.