2.1. Уравнение Ньютона – Рихмана

При проектировании каналов и устройств важно правильно оценивать гидродинамическую обстановку (ламинарное или турбулентное течение), потому, что интенсивность теплоотдачи во многом зависит от структуры и толщины пограничного слоя.

Поверхностная плотность теплового потока для случая ламинарного пограничного слоя может быть определена по закону Фурье

(74)

Однако в большинстве случаев не представляется возможным определить градиент температуры в пограничном слое, а следовательно и определить по формуле (74). Для турбулентного пограничного слоя эта формула вообще не приемлема.

Поэтому в основу расчета конвективного теплообмена принят закон Ньютона Рихмана:

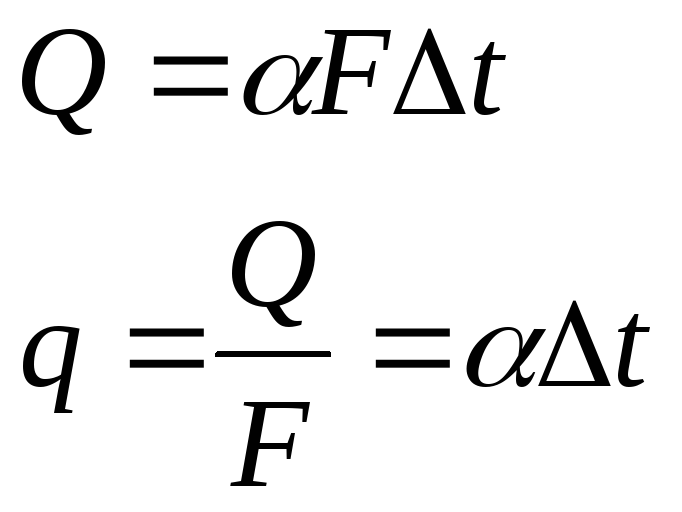
(75)

где, ∆t=t_ж-t_c- средняя разность температур между жидкой и твердой стенкой на всей площади поверхности.

F- поверхность теплообмена

- коэффициент теплоотдачи, характеризующий её интенсивность.

Численно коэффициент теплоотдачи равен тепловому потоку, передаваемому в единицу времени через единицу поверхности при разности температур стенки и жидкости в 1 К.

(76)

Эта количественная характеристика процесса теплоотдачи учитывает его конкретные условия.

Опыт показывает, что αменяется от 0 до 200000

Приведенное нами уравнение (75) было предложено Ньютоном для случая теплообмена в свободном потоке при условии, что зависит только от физических свойств тела и среды. В действительности жекоэффициент теплоотдачи ,в отличие от коэффициента теплопроводности не является величиной постоянной, а зависит от множества факторов, тех же от которых зависит и тепловой поток Q

α=f(ω;t_c;t_ж;λ;ρ;C_p;α;β;µ;l­₁;l₂;…;F­)

Производить расчеты по формуле Ньютона – Рихмана можно только после того, как определен . А в этом заключается основная сложность расчета коэффициента теплоотдачи.

Изучение теплоотдачи ведется двумя взаимосвязанными методами: аналитическим и экспериментальным (опытным)

При аналитическом методе изучения ведется на основе дифференциальных уравнений конвективного теплообмена.

1. 

2. 

3. 

4. 

2.2. Дифференциальные уравнения конвективного теплообмена

Любой физический процесс можно описать дифференциальным уравнением (или интегральным). Учитывая, что теплоотдача осуществляется и теплопроводностью, и конвекцией, зависит не только от температурных условий, но и от характера движения жидкости, поэтому она описывается не одним дифференциальным уравнением, а системой дифференциальных уравнений в которую входят:

- уравнение теплообмена на границе раздела сред;

- дифференциальное уравнение энергии;

- дифференциальное уравнение движения жидкости;

- дифференциальное уравнение неразрывности.

2.2.1. Уравнение теплообмена на границе раздела сред.

Уравнение теплообмена должно характеризовать теплообмен на границе соприкосновения твердого тела и жидкости.

Его можно составить исходя из свойств пограничного ламинарного слоя жидкости, который имеется как при ламинарном и при турбулентном режиме течения.

Учитывая, что в нём нет перемешивания жидкости и теплота передается через него только теплопроводностью по нормали к поверхности к твердому телу плотность теплового потока можно определить по закону Фурье

(77)

λ_ж - коэффициент теплопроводности жидкости

- градиент температуры в пограничном слое

Кроме того плотность теплового потока, передаваемую через пограничный слой можно выразить и через закон Ньютона – Рихмана

q=α∆t (78)

где ∆t=t_с-t_ж

Приравнивая правые части уравнений (77) и (78) мы получим уравнение теплообмена.

(79)

Уравнение (79) связывает коэффициент теплоотдачи αс условиями теплообмена в пограничном слое, т. е. с градиентом температуры.

Для того, чтобы по уравнению (79) определить необходимо знатьgradt, для определения которого нужно знать температурное поле в жидкости. Его нам поможет определить дифференциальное уравнение энергии (или уравнение Фурье – Каргофа – теплопроводность в движущейся жидкости )