2.7.3.3 Особенности расчета коэффициента теплоотдачи при поперечном обтекании пучка оребрённых труб.

Одним из недостатков гладкотрубных теплообменных аппаратов с поперечным омыванием пакета труб являются не высокие коэффициенты теплоотдачи при течении там газов и вязких жидкостей. Этот недостаток влечет за собой существенные увеличения габаритов и массы аппарата.

Компактные теплообменники в этом случае получаются при применении пучков оребренных труб (ленты, пластины, проволочные наклейки, батареи в новых домах).

Наличие оребренных труб в потоке жидкости или газа во – первых, увеличивает поверхность теплообмена, а во – вторых, интенсифицирует теплоотдачу благодаря дополнительной турбулизации потока. Q=α∆tF

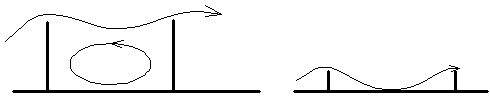
Поэтому при поперечном омывании пучка оребренных труб теплоотдача в них зависит не только от компоновки (шахматная или коридорная). Но и от формы, высоты ребер и шага между ними.

Опытом установлено, что с ростом высоты ребер вследствие снижения их тепловой эффективности α понижается. Поэтому в потоках вязкой жидкости наиболее эффективна малая высота ребер. Однако, для газов повышениепри уменьшенииh_p не компенсирует уменьшение теплоотдачи от удлинения поверхности теплообмена.

Оптимальный размер шага между ребрами колеблется в пределах

t_p=(0,2-0,4)d_тр Уменьшение t_p приводит к уменьшению α, т.к. между ребрами появляются зоны со слабой циркуляцией.

На интенсивность теплоотдачи в пучках оребренных труб значительное влияние оказывает и толщина ребер δ_р. Оптимальнее δ_р по опытным данным составляет 0,5 мм. Увеличение её приводит к ухудшению массовых показателей.

Экспериментальное исследование теплоотдачи в пучках оребренных труб связано с большими трудностями при определении температурных полей в ребрах. Поэтому для упрощения исследований вводится понятие приведенного коэффициента теплоотдачи . Суть его заключается в том, что оребренную поверхность сводят к равновеликой гладкой, а действительные условия эксперимента заменят фиктивными, хотя и эквивалентными по суммарным результатам.

Однако, уравнения подобия выведенные для определения имеют ограниченное применение, т.к. справедливы только для тех условий, в которых проводиться эксперимент. Для того, чтобы результаты единичного эксперимента можно было распространять на целый класс явлений используют конвективный коэффициент теплоотдачи, который учитывает термическое сопротивление собственно ребер. Тепловой поток, при определенииотносится к разности температур между теплоносителем(t_ж) и определенной температурой оребреннных и неоребренных поверхностей трубы

,

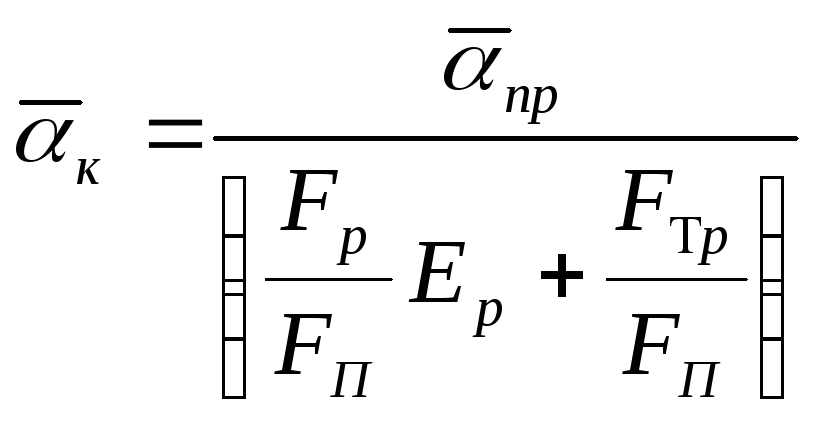где F_p- площадь поверхности ребер на единице длины трубы

F_П - полная площадь поверхности оребренной трубы F_П=F_р+F_тр

F_тр- площадь поверхности трубы.

E_p - коэффициент эффективности ребер, характеризующий их термическое сопротивление E_p=f(t_p;h_p;Ф). Он определяется как отношение теплового потока, проходящего через оребренную поверхность, к тому Q, который мог бы через нее проходить при .

Различные выражения определения E_p и уравнения подобия для расчета поперечного обтекания пучков оребренных труб вы можете, при необходимости, найти в литературе (Селиверстов стр.200)