- •Кинематика материальной точки. Векторный способ описания движения мт
- •2.Кинематика материальной точки. Координатный способ описания движения мт.
- •3. Кинематика материальной точки. Траекторный способ описания мт.
- •4. Среднее и мгновенное значение скорости и ускорения. Нормальное и тангенциальное ускорение при движении по криволинейной траектории.
- •5. Классификация движений мт. Понятие о степенях свободы. Кинематика поступательного и вращательного движений твёрдого тела. Понятие о мгновенном центре скоростей.
- •6. Векторы угловой скорости и углового ускорения твёрдого тела. Связь угловых и линейных кинематических величин.
- •7. Основная задача динамики. Понятия массы, импульса и силы. Законы Ньютона.
- •8 . Преобразования Галилея. Принцип относительности Галилея.
- •9. Динамика системы материальных точек. Закон сохранения импульса.
- •1 0. Реактивное движение. Уравнение Мещерского. Формула Циолковского.
- •11. Центр масс, уравнение его движения.
- •12. Момент силы и момент импульса для мт и системы мт. Проекция момента силы и импульса на ось.
- •13. Законы сохранения импульса и момента импульса как отражение свойств пространства.
- •14. Закон всемирного тяготения. Сохранение момента импульса при движении в поле центральных сил.
- •15.Основное уравнение динамики вращательного движения.
- •16. Момент инерции. Свойство аддитивности. Теорема Штейнера. Свободные оси вращения. Понятие о гироскопе его применениях.
- •17. Работа при поступательном и вращательном движении. Мощность.
- •18. Кинетическая энергия. Закон изменения кинетической энергии.
- •19. Консервативные и неконсервативные силы. Потенциальная энергия. Понятие о потенциальном поле. Потенциальная яма.
- •20. Неконсервативные силы, диссипация механической энергии. Примеры неконсервативных сил.
- •21. Потенциалы гравитационной силы, силы упругости и силы тяжести. Консервативные системы, закон сохранения механической энергии.
- •Закон сохранения механической энергии
- •22. Законы столкновения/соударения. Импульс силы.
- •23. Статика. Условия равновесия абсолютно твёрдого тела. Понятие связей в механике. Реакции связей.
- •24. Колебания. Гармонические колебания. Закон движения при гармонических колебаниях. Скорость и ускорение при гармонических колебаниях.
- •25. Силы, действующие на осциллятор. Дифференциальное уравнение гармонических колебаний. Превращение энергии при гармонических колебаниях. Энергия гармонического осциллятора.
- •26. Формы представления гармонических колебаний. Простые осцилляторы (физический, математический и пружинный маятники).
- •27. Сложение колебаний методом векторных диаграмм. Биения.
- •28. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
- •29. Затухающие колебания. Дифференциальное уравнение затухающих колебаний.
- •30. Вынужденные колебания. Резонанс. Дифференциальное уравнение вынужденных колебаний.
- •32. Стоячие волны. Уравнение стоячей волны. Спектр частот колебаний струны.
- •33.Энергия волны. Вектор Умова.
- •34. Звук, инфра- и ультразвук. Эффект Доплера.
- •35. Границы применимости классической механики. Постулаты специальной теории относительности. Преобразования Лоренца.
- •36. Следствия преобразований Лоренца: сокращение размеров тел в направлении их движения; замедление хода времени в движущейся системе отсчёта.
- •1 Следствие: сокращение размеров тел в направлении их движения.
- •2 Следствие: замедление хода времени в движущейся системе отсчёта:
- •37. Следствия преобразований Лоренца: относительность одновременности; инвариантность интервала между двумя событиями.
- •38. Закон преобразования скоростей в релятивистской механике.
- •39. Импульс релятивистской частицы. Основной закон релятивистской динамики.
- •40. Энергия в релятивисткой механике. Закон взаимосвязи массы и энергия. Масса покоя.
- •41. Понятие о квантовой механике. Корпускулярно-волновой дуализм. Волна де Бройля. Принцип суперпозиции состояния. Волновая функция и её статистический смысл.
- •42. Соотношение неопределённостей Гейзенберга. Тождественность и спин частиц. Временное и стационарное уравнение Шредингера.
- •43. Решение стационарного уравнения Шредингера для свободной частицы.
- •45. Решение стационарного уравнения Шредингера для гармонического осциллятора. Нулевая энергия.
- •46. Туннельный эффект.
- •48. Работа в термодинамике. Уравнение состояния вещества. Уравнение Клапейрона- Менделеева. Газовые законы. Первое начало термодинамики.
- •49.Адиабатический процесс. Уравнение адиабаты.
- •50. Вычисление работы и внутренней энергии идеального газа для изотермического, изобарического, изохорического и адиабатического процессов.
- •Внутренняя энергия идеального газа
- •51. Теплоёмкость вещества. Изобарическая и изохорическая теплоёмкость. Уравнение Майера.
- •52. Теплоёмкость и внутренняя энергия идеального газа.
- •53. Циклические процессы. Прямой и обратный циклический процесс. Цикл Карно. 1-я и 2-я теоремы Карно. Циклические процесс как основа работы тепловых машин.
- •54. Второе начало термодинамики. Формулировки второго начала термодинамики. Понятие обратимого и необратимого процессов.
- •55. Неравенство Клаузиуса. Энтропия. Статистический вес макроскопических состояний. Формула Больцмана. Свойства энтропии.
- •56. Принцип возрастания энтропии. Третье начало термодинамики. Основное уравнение термодинамики.
- •3 Начало термодинамики. 1906-теорема Нернста.
- •57. Термодинамические функции равновесного состояния системы. Взаимосвязь функций состояния («Энергетический пирог»).
- •58. Модель идеального газа. Закон Максвелла для распределения молекул по скоростям теплового движения. Вычисление средних величин с использованием функций распределения.
- •59. Основное уравнение молекулярно-кинетической теории газов. Давление. Молекулярно-кинетический смысл температуры. Следствия из основного уравнения мкт.
- •61. Закон Больцмана для распределения частиц в потенциальном поле. Барометрическая формула.
- •62.Понятие о статистических распределениях Ферми-Дирка и Бозе-Эйнштейна. Переход к классическому распределению при высоких температурах.
- •64. Уравнение Клапейрона-Клаузиуса. Правило Максвелла для равновесия в точке фазового перехода.
- •6 5. Силы и потенциальная энергия межмолекулярного взаимодействия. Межмолекулярный потенциал Леннард-Джонса. Уравнение Ван-дер-Вальса.
- •67. Внутренняя энергия реального газа (газа Ван-дер-Вальса). Сжижение газов и получение низких температур.
- •68. Эффект Джоуля – Томпсона. Кривая инверсии.
- •69. Строение твёрдых тел и их основные свойства. Симметрия и дефекты кристаллической решетки. Деформация.
15.Основное уравнение динамики вращательного движения.
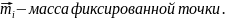


0
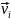

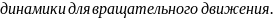
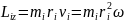 (v=rw)
(v=rw)
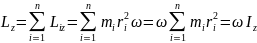
- Произведение угловой скорости на момент инерции тела относительно оси z есть момент импульса.
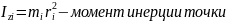
Т.о.

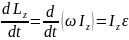

16. Момент инерции. Свойство аддитивности. Теорема Штейнера. Свободные оси вращения. Понятие о гироскопе его применениях.
Момент инерции тела относительно некоторой оси при вращательном движении представляет собой меру инертности системы.
Величина момента инерции зависит от распределения массы.
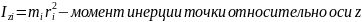
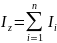
Если тело протяжённое, то суммарный момент инерции рассчитывается путём замены суммы на интеграл.
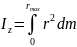
Свойство аддитивности: момент инерции системы МТ относительно некоторой оси равен сумме моментов инерции тел или частей системы (МТ) относительно этой оси.
Теорема
Гюйгенса-Штейнера:
момент инерции
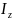 тела
относительно произвольной оси равен
сумме момента инерции этого тела
относительно параллельной ей оси
тела
относительно произвольной оси равен
сумме момента инерции этого тела
относительно параллельной ей оси
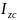 ,
проходящей через центр масс, и произведения
массы тела на квадрат расстояния d
между этими осями.
,
проходящей через центр масс, и произведения
массы тела на квадрат расстояния d
между этими осями.
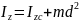





C
m
d
Л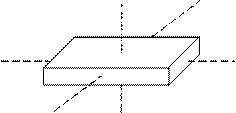 юбое
тело произвольной формы имеет три
взаимно перпендикулярных оси, проходящих
через центр масс, которые называют свободными
осями вращения, или
главными осями инерции.
юбое
тело произвольной формы имеет три
взаимно перпендикулярных оси, проходящих
через центр масс, которые называют свободными
осями вращения, или
главными осями инерции.
Например, для параллелепипеда главными осями инерции являются три оси, которые проходят через центры противоположных граней.
Свойство свободных осей сохранять своё положение в пространстве используется в гироскопах.
Гироскопы представляют собой массивные однородные тела, которые с большой угловой скоростью вращаются вокруг своей оси симметрии, которая является свободной осью. Сила тяжести не может изменить ориентацию оси вращения, так как сила приложена к центру масс, и момент силы относительно центра масс равен нулю. Таким образом, как ни вращать гироскоп, направление его оси вращения
останется неизменным в пространстве. Простейший пример гироскопа — юла. Гироскопы используются в навигации (авиагоризонт, гирокомпас) и в системах ориентации и стабилизации космических аппаратов.
17. Работа при поступательном и вращательном движении. Мощность.
Е сли
сила, действующая на тело, перемещает
его на некоторое расстояние, то говорят,
что сила совершает работу.
сли
сила, действующая на тело, перемещает
его на некоторое расстояние, то говорят,
что сила совершает работу.
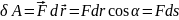
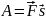
Вывод о том, какова будет величина работы:
Если угол между направлениями силы и перемещения лежит в пределах
 ,
то сила будет называться движущей,
а работа будет положительной
,
то сила будет называться движущей,
а работа будет положительной
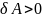 .
.Если
 , то сила – тормозящая,
а работа отрицательна
, то сила – тормозящая,
а работа отрицательна
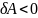 .
.Если
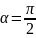 (сила перпендикулярна перемещению)
,то работа не совершается
(сила перпендикулярна перемещению)
,то работа не совершается
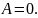
Чтобы найти полную работу (при поступательном движении), необходимо произвести интегрирование:
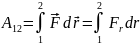

Выражение, которое мы получили для МТ, можно применять и для абсолютно твёрдого тела. В этом случае под величиной перемещения следует понимать перемещение точки приложения сил.
Если на тело действует одновременно несколько сил, то каждая из них совершает работу, а суммарная работа равна сумме работ приложенных сил.
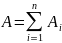
Работа при вращательном движении:
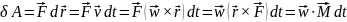
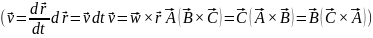
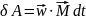
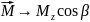
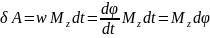
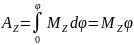
Скорость работы определяется мощностью. Мощность – это работа, совершаемая в единицу времени.