6. Векторы угловой скорости и углового ускорения твёрдого тела. Связь угловых и линейных кинематических величин.

Вращательное движение – движение, при котором все точки движутся по окружностям, центры которых лежат на одной неподвижной прямой, которая называется осью вращения.

Чтобы определить скорость изменения координаты, нужно ввести угловую скорость:

Угловой скоростью тела называется вектор, численно равный первой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта.

При равномерном вращении угловая скорость не изменяется со временем, то есть является постоянной величиной (ω = const).

Равномерное вращение характеризуется периодом вращения и частотой вращения.

Период вращения − это время, за которое точка совершает один полный оборот, т. е. поворачивается на угол ϕ = 2п.

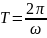
Ч

астота вращения − это число полных оборотов, которое делает точка при равномерном вращении, за единицу времени:

(Неравномерное движение) Угловым ускорением называется векторная величина, равная

первой производной угловой скорости по времени:

Если угловая скорость увеличивается, то , а если замедляется, то

α

7. Основная задача динамики. Понятия массы, импульса и силы. Законы Ньютона.

Динамика – раздел физики, изучающий общие свойства движения тел, возникающего под воздействием приложенных к ним сил.

Основная задача динамики – определить положение тела в любой момент времени.

В динамике изучается не движение МТ, а движение реальных тел, которые характеризуются такими величинами как масса и импульс.

Инерциальная система отсчёта – такая система отсчёта, в которой тело находится либо в состоянии покоя, либо движется прямолинейно и равномерно (без ускорения).

Любая система отсчёта которая движется относительно первой равномерно и прямолинейно является ИСО.

Инерция – свойство тел сохранять состояние покоя или двигаться равномерно и прямолинейно.

Масса - количественная мера инерции тела. Она проявляется как мера инертности тела при попытке изменить его скорости. – инертная масса. [m] = кг. Масса − величина аддитивная, т. е. масса тела равна сумме масс всех частей этого тела.

Если тело имеет инертную массу и движется с определённой скоростью, то ему присущ импульс. Импульс тела (или количество движения) − это векторная физическая величина, равная произведению массы тела на его скорость:

Единица измерения импульса в СИ −

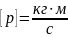
Сила − это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело деформируется или приобретает ускорение.

Единица измерения силы в СИ − .

Первый закон Ньютона (или закон инерции). Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока действие со стороны других тел не выведут его из этого состояния.

Системы отсчёты в которых выполняется закон инерции называются инерциальными системами отсчёта. Системы отсчета, по отношению к которым первый закон Ньютона не выполняется, называются неинерциальными системами отсчета.

Второй закон Ньютона: ускорение тела прямо пропорционально результирующей сил приложенных к нему и обратно пропорционально его массе.

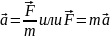
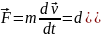
Скорость изменения импульса материальной точки равна действующей на нее силе.

Второй закон Ньютона позволяет решать основную задачу механики. Поэтому его называется основным уравнением динамики поступательного движения.

Третий закон Ньютона (или закон парности взаимодействия). Сила, с которой одно тело действует на другое, равна по величине и противоположна по направлению силе, с которой второе тело действует на первое.

П ри взаимодействии трёх тел первое тело действует на второе, второе действует на первое и на третье, а третье на второе. Действия сил носят независимый характер.

1 2 3