45. Решение стационарного уравнения Шредингера для гармонического осциллятора. Нулевая энергия.

В тех случаях, когда частица находится в стационарных потенциальных силовых полях, ур-ние Шредингера можно представить: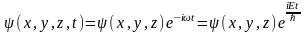 ,где Е-полная энергия частицы, которая в случае стационарного поля остается неизменной. Подставим данную ф-цию в ур-ние Шредингира: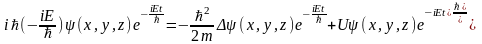 .Сократив и преобразовав ур-нение, получим стационарное ур-ние Шредингера: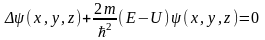

_{Нулевая энергия} — минимальный уровень энергии, который может иметь данная квантовомеханическая система. Частица может находиться в точке, отвечающей минимуму потенциала энергии и иметь нулевую кинетическую энергию. В этом случае частица находится в состоянии устойчивого равновесия и имеет минимальную энергию, равную потенциальной энергии в точке равновесия. Нулевая энергия используется как синоним для энергии вакуума.

46. Туннельный эффект.

Т уннелирование – прохождение микрочастицы через потенциальный барьер. Потенциальный барьер – область пространства от 0 до Х, где потенциальная функция имеет большее значение, чем в соседних областях.

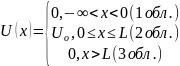
Коэффициент потенциальности:

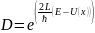
Выражения для уравнения Шредингера для областей 1,3 и 2 будут отличаться: для 1,3: 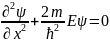для 2:

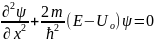
Ψ₁(x)=A₁e^ikx+B₁е^-ikx (область 1);

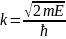
Ψ₂(x)=A₂e^iqx+B₂е^-iqx (область 2);

Ψ₃(x)=A₃e^ikx+B₃е^-ikx ; в общем решении B₃е^-ikx →0 (область 3).

Особенности квантовой механики:

1. Все частицы – тождественные величины.

2. В зависимости от вида потенциальной ф-и, отношение Е потенциальной ф-и и Е частицы изменяются.

3. Т.к. вид потенциальной ф-и всегда отличается от теор. бескон. глубины потенциальной ямы, то обнаруживается ненулевая вероятность нахождения частицы за пределами потенциальной ямы.

47. Основные принципы термодинамики. Понятие внутренней энергии, состояния, системы, процесса. Равновесные и неравновесные процессы. Первое начало термодинамики для изотермического, изобарического, изохорного и адиабатического процессов.

Термодинамика изучает макросистемы (системы которые состоят из очень большого числа частиц) не интересуясь их внутренним строением. При таком подходе для характеристики систем используется понятия и сведения величин, которые относятся к системе в целом. И эти величины могут быть непосредственно изменены в эксперименте.

Термодинамика опирается на 2 принципа, которые представляют собой обобщение совокупностей экспериментальных данных: 1.Принцип эквивалентности теплоты и работы: если над системой совершается работа, то она может быть определена через изменение характеристик, характеризующих количество теплоты, полученной либо отданное системой. 2.Самопроизвольный переход теплоты в системе является односторонним (однонаправленным). Происходит от нагретых тел к холодным.

Выводы термодинамики не зависят от наших представлений о микроструктуре вещества, поскольку они – следствия основных положений термодинамики, надёжность выводов определяется надёжностью исходных принципов.

Термодинамика и МКТ (молекулярно-кинетическая теория) оперируются своим набором понятий и величин.

Система – это любое тело или совокупность тел, свойства которых рассматриваются в данной задаче. Если тело не входит в систему, то оно называется внешним телом. Если взаимодействием системы с внешними телами можно пренебречь, то такую систему называют замкнутой, т.е. система изолирована. С истема будет незамкнутой (неизолированной), если есть взаимодействие с внешними телами.

Состояние системы определяется совокупностью измеренных физ. величин, которые называются параметрами системы. Они позволяют полностью описать состояние системы. В термодинамики это P,T,V. (P,Т – внутренние параметры, их величина зависит от свойств самой системы. V – внешний параметр. Это величина характеризует свойство системы в зависимости от наличия взаимодействия с внешними телами либо от величины взаимодействия внешних сил.)

Состояния системы разделяют на равновесные, если при отсутствии внешних воздействий все параметры системы сохраняют свои значения сколь угодно долго. Неравновесные, если параметры системы будут изменяются во времени.

Процесс - переход из одного состояния системы в другое. Процессы могут быть равновесные (если в ходе изменения состояния системы в любой момент времени состояние системы является равновесным); если переход из одного состояния в другое может происходить достаточно медленно, то состояние в каждый момент времени можно считать равновесным. Большинство процессов в системе неравновесные.

Только равновесные процессы можно изображать графически в системе координат, которые отражают термодинамические параметры, неравновесные процессы представить т.о. нельзя.

Равновесные процессы = квазистатические = медленно изменяющиеся.

Внутренняя энергия U системы - это сумма кинетической энергии хаотического движения частиц и потенциальной энергий их взаимодействия друг с другом. Внутренняя энергия является функцией состояния системы. Это означает, что всякий раз, когда система оказывается в состоянии с заданными значениями V и Т, ее внутренняя энергия принимает присущее этому состоянию значение, независимо от того, каким способом система приведена в это состояние.

Существует некая функциональная зависимость между термодинамическим состоянием системы. И эта функция есть уравнение состояния системы.

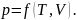
Состояние системы можно изменить 2 способами:

1. совершить некую работу над системой или предоставить системе возможность самой совершать работу.

2. осуществить теплообмен системы с внешними телами.

Идеальный газ – это газ, подчиняющийся

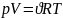
Первое начало термодинамики Q=∆U+A

Количество теплоты, которое сообщается системе идёт на приращение её внутренней энергии и на совершение системой работы над внешними телами.

1 .Изотермический процесс: Т=соnst; PV=const ⇒ P=const/V (Закон Бойля-Мариотта: PV=const)

U(T)=νC_vT⇒dU=0;δQ= δA ⇒

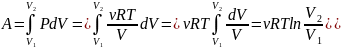
2 .Изобарический: P=const; V/T = const ⇒ V=T const (Закон Гей-Люссака V/T = const)

δQ=dU+ δA; δQ= νC_vT+δA; 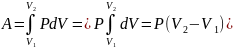; U=νC_v∆T

3 .Изохорный процесс: V= const Р/T = const ⇒ Р=T const (Закон Шарля Р/T = const)

dV≡0 ⇒ δA≡0; δQ= dU; 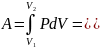0; ∆U=νC_v∆T

4.Адиабатический процесс - процесс который происходит без теплообмена с окружающей средой.

И зменение внутренней энергии системы численно равно значению работы, взятой с противоположным знаком. Если система совершила работу, то значение ∆U – убыло. В адиабатном процессе вся работа совершается за счёт внутренней энергии газа.

PV^γ=const – Уравнение Пуассона или уравнение адиабаты.

ТV^γ-1=const Т^γР^1-γ=const - выражения для уравнения Пуассона

Адиабатический процесс при Q=0:

δQ=0 ⇒ dU=-δA ⇒ U=-A ⇒ A=-U=-νC_v(T₂-T₁)

∆U=νC_v∆T