29. Затухающие колебания. Дифференциальное уравнение затухающих колебаний.

З атухающие колебания – колебания, амплитуда которых непрерывно уменьшается вследствие потери энергии. В реальности все колебания затухающие.

Дифференциальное уравнение для идеализированного случая:

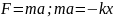
Для затухающих колебаний:

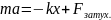
Силы затухания пропорциональны скорости.

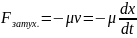
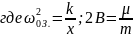
Е сли затухание небольшое, то решением этого дифференциального уравнения будет функция, похожая по форме на функцию для свободных колебаний:

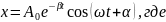
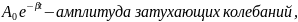
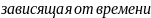
Частота затухающих колебаний несколько отличается от частоты свободных гармонических колебаний: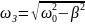

Для характеристики скорости затухания вводят такое понятие, как время релаксации (затухания). То время, за которое амплитуда колебаний меняется (уменьшается) в е раз.

Декремент затухания – это отношение значений амплитуд, соответствующих моментам времени, отличающимся на период.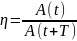

Для характеристики колебательной системы обычно используется логарифмический декремент затухания, т. е. логарифм декремента затухания:

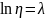
Если колебания затухающие, то при наличии у осциллятора определённой энергии число колебаний лимитировано. За время релаксации система τ успевает совершить N колебаний:

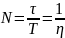
Добротность Q – это отношение запасённой (сообщённой) энергии осциллятором к энергии, которую он расходует на совершение одного колебания.

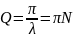
Величина Q, пропорциональная числу колебаний, совершаемых системой за время, в течение которого амплитуда колебаний уменьшается в е раз.

30. Вынужденные колебания. Резонанс. Дифференциальное уравнение вынужденных колебаний.

Вынужденные колебания – движение колебательной системы под действием внешней периодической силы.

На материальную точку в инерциальной системе действуют

• возвращающая сила

• сила сопротивления среды

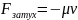
• вынуждающая внешняя сила .

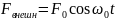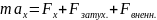
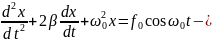
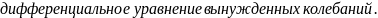
Закон, которому подчиняются колебания: амплитуда зависит от частоты вынуждающей силы; начальная фаза – функция частоты вынуждающей силы.

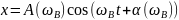
Метод векторных диаграмм.

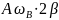
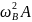
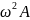
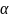
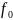
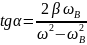
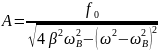
Эти величины не являются постоянными, зависят от частоты собственной и частоты вынужденной.

Очевидно, что зависимость амплитуды от частоты внешней вынуждающей силы должна иметь некий экстремум, при совпадении собственной частоты и вынужденной частоты функция будет иметь максимум.

Резонанс- явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты осциллятора с вынуждающей частотой.

Условия резонанса:

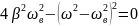
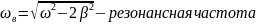
При резонансной частоте наблюдается максимальное значение амплитуды.

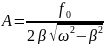
Амплитудно-частотная характеристика(АЧХ) является по своей сути функцией, показывающей зависимость на выходе амплитуды от частоты гармонического сигнала на входе.

В зависимости от величины затухания положение максимума будет меняться как по амплитуде, так и по частоте.

В предельном случае, если затухание много меньше , то отношение 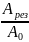не что иное как добротность. 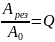. Добротность Q – это отношение запасённой (сообщённой) энергии осциллятором к энергии, которую он расходует на совершение одного колебания.

31. Волновое движение. Уравнение плоской бегущей волны. Волновое уравнение. Колебания частиц среды, которые распространены в пространстве в течение времени называется волновым процессом или волной. Любая волна, независимо от её природы переносит энергию, но не переносит вещество. Различают: продольные волны - колебания совершаются в том же направлении, что и направление распространения волны (деформация в твёрдых телах, жидкостях, газах). Поперёчные волны – колебания совершаются в направлении, перпендикулярном направлению волны. В твёрдых телах может наблюдаться деформация сдвига поперёчной волны. Фронт волны – геометрическое место точек в пространстве, до которого возмущение, передаваемое волной, распространяется за какой-то промежуток времени t. Волновая поверхность – геометрическое место точек среды, которые совершают колебания в одинаковой фазе. Волновая поверхность и фронт волны всегда перпендикулярны направлению распространения волны, которое можно назвать понятием луч. Длинна волны λ - расстояние, на которое перемещается волна за время одного колебания.

Рассмотрим два предельных вида волн: плоские и сферические. Плоские характеризуются фронтом с бесконечно большим радиусом кривизны, плоским фронтом и амплитудой, которая с течением времени не изменяется. Сферическая волна – сферическая форма волн фронта, имеют точечный источник, амплитуда убывает по мере увеличения расстояния от волнового фронта до источника.

Р ассмотрим первый тип волн – бегущие волны. Плоская бегущая волна которая имеет определённую частоту ω. S=S(x; t) . Уравнение плоской волны:

В случае сферической волны: при распространении сферической волны, протяжённость волнового фронта увеличивается, энергия, которую переносит волна, распространяется по большому пространству, амплитуда по мере удаления от источника уменьшается.

В декартовых координатах волновое уравнение: Скорость распространения зависит от процессов, в которые вовлечены частицы среды. Скорость распространения продольной волны: Для волновых процессов справедлив принцип суперпозиции: при распространении волны в среде нескольких волн колебания точек среды определяется суммой колебаний, которые совершили бы частицы среды при распространении каждой из волн в отдельности.