1. Кинематика материальной точки. Векторный способ описания движения мт

Механика – раздел физики, который изучает движение и взаимодействие тел.

Кинематика - раздел механики, изучающий движение тел без учёта причин его вызвавших.

Основная задача кинематики – расчёт кинематических характеристик движущихся объектов, к которым относятся скорость, ускорение и траектория.

Для описания движения необходимо выбрать систему отсчета. Система отсчета состоит из тела отсчета и системы пространственных координат, снабженной часами и связанной с телом отсчета. Тело отсчета − произвольно выбранное, в идеале – абсолютно твердое тело, относительно которого определяется положение остальных тел.

С уществует 3 способа описания кинематики материальной точки.

Векторный способ описания движения МТ.

Если есть некое тело отсчёта, то движение тела может быть описано с помощью радиус-вектора. Зависимость радиус-вектора от времени - закон движения МТ: .

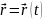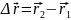– перемещение МТ.

Средняя скорость – величина, равная отношению перемещения к интервалу времени, за который произошло это перемещение.

Мгновенная скорость – скорость, характеризующая движение материальной точки в любой определённый момент времени.

Средняя путевая скорость – отношение перемещения к интервалу времени, за который это перемещение произошло.

где s – расстояние, пройденное материальной точкой по траектории.

С реднее ускорение – отношение изменения средней скорости к интервалу времени.

Мгновенное ускорение.

З адачи:

ПРЯМЫЕ:

О БРАТНЫЕ: (необходимо знать начальные условия)

2.Кинематика материальной точки. Координатный способ описания движения мт.

Механика – раздел физики, который изучает движение и взаимодействие тел.

Кинематика - раздел механики, изучающий движение тел без учёта причин его вызвавших.

Основная задача кинематики – расчёт кинематических характеристик движущихся объектов, к которым относятся скорость, ускорение и траектория.

Для описания движения необходимо выбрать систему отсчета. Система отсчета состоит из тела отсчета и системы пространственных координат, снабженной часами и связанной с телом отсчета. Тело отсчета − произвольно выбранное, в идеале – абсолютно твердое тело, относительно которого определяется положение остальных тел.

С уществует 3 способа описания кинематики материальной точки.

Координатный способ описания движения материальной точки.

Система координат характеризуется единичными векторами.

Перемещение может быть представлено как результат трех независимых перемещений вдоль координатных осей: x = x ( t ), y = y ( t ), z = z ( t ). Т.е. общий закон движения МТ можно разбить на 3.

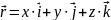
Воспользовавшись теоремой Пифагора, получаем:

Скорость:

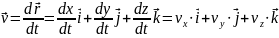
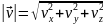
Ускорение:

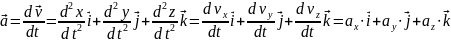
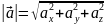
Можем рассмотреть обратную задачу. Для этого необходимо знать:

3. Кинематика материальной точки. Траекторный способ описания мт.

Механика – раздел физики, который изучает движение и взаимодействие тел.

Кинематика - раздел механики, изучающий движение тел без учёта причин его вызвавших.

Основная задача кинематики – расчёт кинематических характеристик движущихся объектов, к которым относятся скорость, ускорение и траектория.

Для описания движения необходимо выбрать систему отсчета. Система отсчета состоит из тела отсчета и системы пространственных координат, снабженной часами и связанной с телом отсчета. Тело отсчета − произвольно выбранное, в идеале – абсолютно твердое тело, относительно которого определяется положение остальных тел.

Существует 3 способа описания кинематики материальной точки.

Траекторный способ описания движения МТ.

Используется, если траектория движения заранее известна. Необходимо определить начальную точку (откуда тело начинает движение) и направление движения.

l – перемещение вдоль траектории. Это естественная координата, меняющаяся со временем.

l(t) - закон движения.

Чтобы описать движение в т.1 вводим единичный вектор 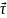, переменного направления по траектории( .

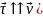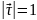
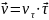
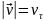
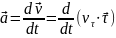
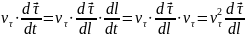
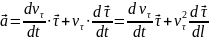
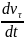( - показывает, как изменяется модуль скорости вдоль траектории; ).
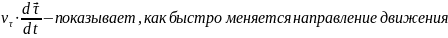