3. Методы определения весовых коэффициентов.

Прием 1.

Для каждого частного критерия вычисляется коэффициент относительного разброса:

( 11.2.0 )

где

, иначе прием 1 применять нельзя.

Для того, чтобы вычислить необходимо решить соответствующие задачи однокритериальной оптимизации. Не всегда это удается, поэтому в формуле ( 11.2 .0 ) допустимо использование оценок этих величин. Далее весовые коэффициенты вычисляются по формуле

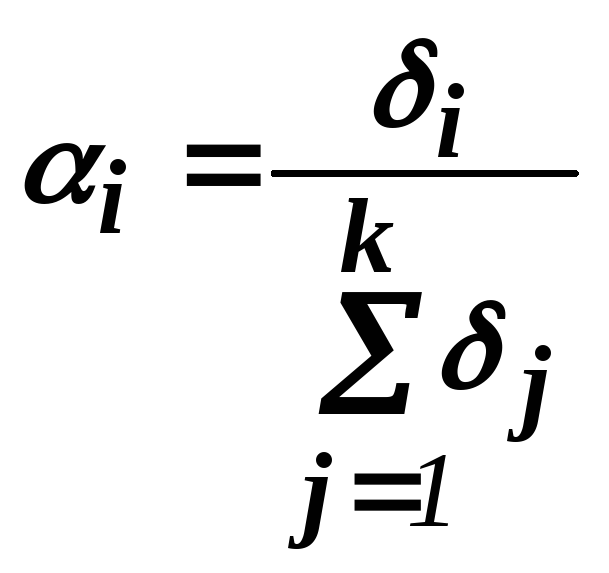(11.2.0 )

При таком подходе в обобщенном критерии "большой вес" имеют те критерии, у которых минимальное значение частного критерия сильно разнится от максимального. Действительно, если - близки, то при любом полученное решение будет близко к. И, наоборот, чем больший разброс имеет некоторый критерий , тем с большим весом его необходимо взять в линейной свертке. В предельном случае, когда

, то есть такой критерий не следует включать в обобщенный.

Вернемся к примеру ( 11.1 .0 ) и применим к нему прием 1 :

Выше для этого примера мы получили общий вид решения:

в зависимости от .

Наконец получаем: .

Получили одну из эффективных точек для задачи ( 11.1 .0 ).

Замечание 1.

Следует обратить внимание на то, что при таком подходе "важность" критерия полностью определяется поведением функции на области.

Прием 2.

Может применяться при условии . Вводятся в рассмотрение вспомогательные функции:

которые можно рассматривать как относительное отклонение частного критерия от его наименьшего значения.

Важность - го критерия определяется через неравенство:

, где задает постановщик задачи:

чем важнее критерий, тем меньше . Затем для каждого критерия вычисляется радиус шара , имеющего

центром , являющуюся решением задачи:

,

внутри которого выполняются условия: .

Далее вычисляются по формуле:

.

При таком подходе важность критерия определяется двумя факторами:

• выбор величины ;

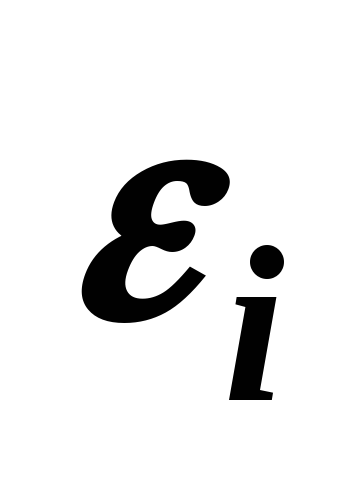• видом функции .

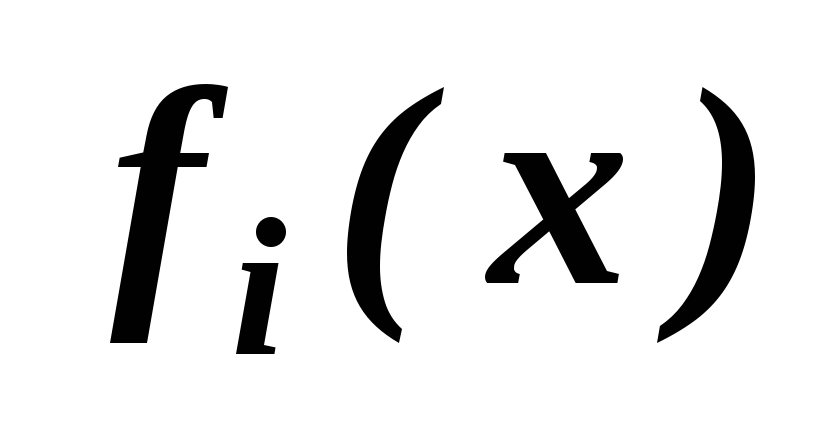Это является бесспорным достоинством метода. Проиллюстрируем на нашем примере ( 11.1 .0 ):

Назначим .

На этом этапе мы не даем ни одному из двух критериев никакого предпочтения.

.

В результате получили, что 1-й критерий оказался важнее 2-го.

Замечание.

Приемы 1, 2 имеют довольно ограниченное применение , так как в силу необходимости решения целой серии однокритериальных задач, кроме того определяющим является вид функции .

Прием 3. Использование попарных приоритетов.

В продолжение последнего замечания следует отметить, что часто не вид функции является решающим в определении важности критериев, а сама сущность проблемы, то есть степень важности одного критерия по сравнению с другим определяется не из математической постановки задачи ( 11.1 .0 ), а путем привлечения дополнительной информации.

Наиболее приемлемым подходом является попарное сравнение критериев по важности в количественном выражении.

Попарное сравнивание критериев по предпочтению между собой должно быть выражено числовыми оценками в виде обыкновенной дроби. Например,означает, что второй критерий "важнее" третьего враза , а третий критерий "менее важен" второго тоже в раза .

По имеющейся информации о степени предпочтения, по важности каждой пары частных критериев составляется матрица размерности, где

равно числителю

равно знаменателю

Например, имеем трехкритериальную задачу, причем выяснили, что первый критерий важнее второго, третий критерий важнее второго, первый важнее третьего. В нашем случае первый критерий важнее третьего и второго, то есть следует ожидать, что наибольшим будет .

Зададимся конкретными данными:

.

.

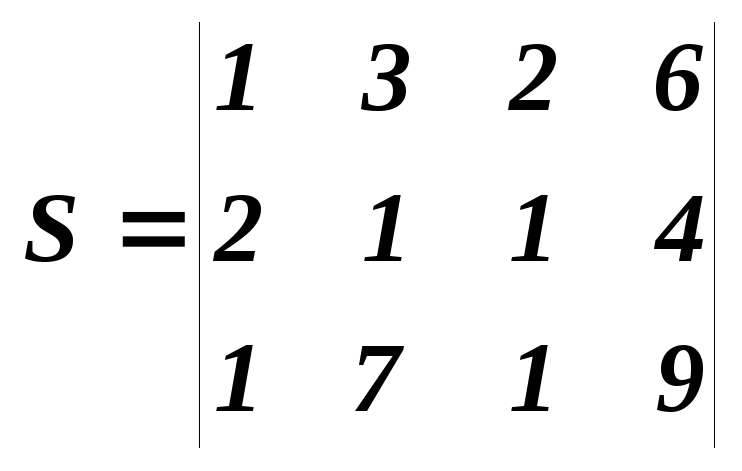
Вопреки ожиданиям, наибольшим получили .

Дело в том, что здесь сыграли роль именно количественные показатели:

третий критерий важнее второго в раз. При определении надо быть очень внимательным. Например, для , если мы четко знаем, что самым важным является первый критерий, затем второй, и, наконец, третий, то для определенияданным приемом можно воспользоваться, нодолжны в этом случае удовлетворять условиям: .

Вернемся к нашему примеру ( 11.1 .0 ) и представим в виде таблицы решения, полученные с помощью линейной свертки, применяя прием 3 при различных .

Прием 4. Использование интервальной информации.

Одним из подходов, наиболее отвечающим практике, является интервальное задание весовых коэффициентов , то есть задание,,, где,- соответственно нижняя и верхняя граница для:.

С постановочной точки зрения этот подход предпочтительнее предыдущих.

Математически он приводит к решению следующей однокритериальной задачи с переменными:

В качестве примера снова рассмотрим задачу ( 11.1 .0 ) при условиях :

Для этого необходимо решить такую задачу:

Такую задачу пришлось решать численно и получено:

Замечание.

Как и в предыдущих приемах , в общем случае, гарантий того, что получено эффективное решение, нет .

Прием 5. Теоретико-игровая модель выбора весовых коэффициентов.

В этом способе выбора весовых коэффициентов используют элементы матрицы :

где

- точка оптимума - того частного критерия.

Значения характеризуют влияние решенияна частный критерий.

Очевидно, что

, а

поскольку мы берем по абсолютной величине.

Строится матрица , она будет квадратной:

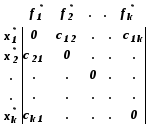
Эту матрицу рассматривают как матрицу платежей в игре двух лиц с нулевой суммой.

Каждой строке соответствуют оптимальные решения по каждому частному критерию, а столбцам соответствуют оптимальные значения частных критериев оптимальности.

Партию игры можно представить следующим образом:

первый игрок может выбрать одну из чистых стратегий , а второй игрок выбирает одну из чистых стратегий.

В этой игре «maxmin» равен 0, а «minmax» равен

то есть игра не имеет седловой точки.

Это означает, что оптимальное решение игры следует искать в форме смешанных стратегий, то есть:

для первого игрока каждая стратегия

выбирается с вероятностью ,

выбирается с вероятностью ,

...........................................................

выбирается с вероятностью

.

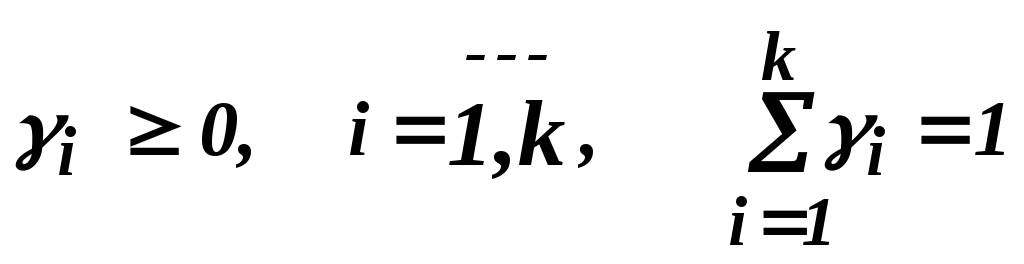Для второго игрока с вероятностями

выбирается с вероятностью ,

выбирается с вероятностью ,

...........................................................

выбирается с вероятностью

.

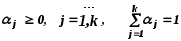Смешанная стратегия второго игрока может быть найдена из решения задачи линейного программирования, представленной в виде:

Решая эту задачу и получив значения находят значения:

.

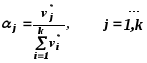В качестве примера снова рассмотрим задачу ( 11.1 .0 ):

Матрица принимает вид:

Решаем задачу вида:

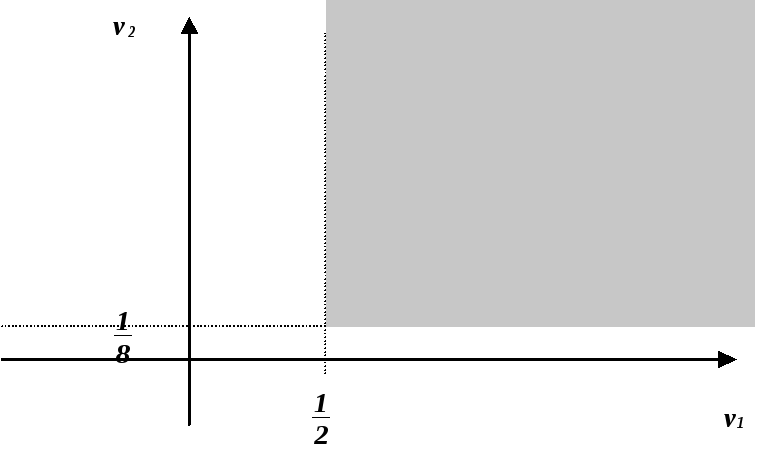
Графически решая ее получаем:

,

Следовательно:

Прием 6. Определение весовых коэффициентов по разности максимального и минимального элемента матрицы .

- это матрица предпочтений.

Используется матрица , построенная по алгоритму, изложенному в приеме 5.

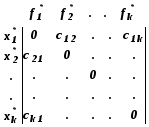
где

Вычисляются:

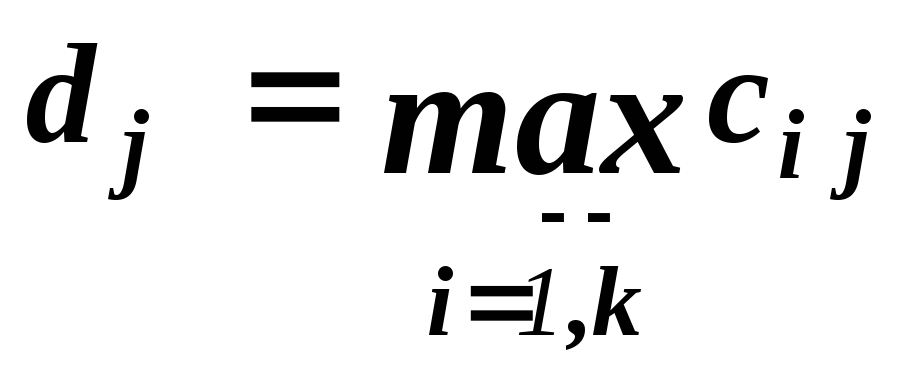
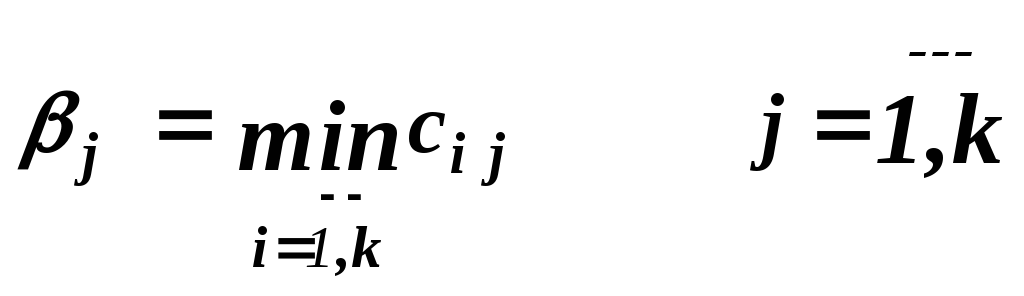
Далее вычисляются:

Значения таким образом вычисляют по формуле:

.

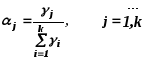Вернемся к примеру ( 11.1 .0 ) и применим к нему прием 6 :

Матрица принимает вид:

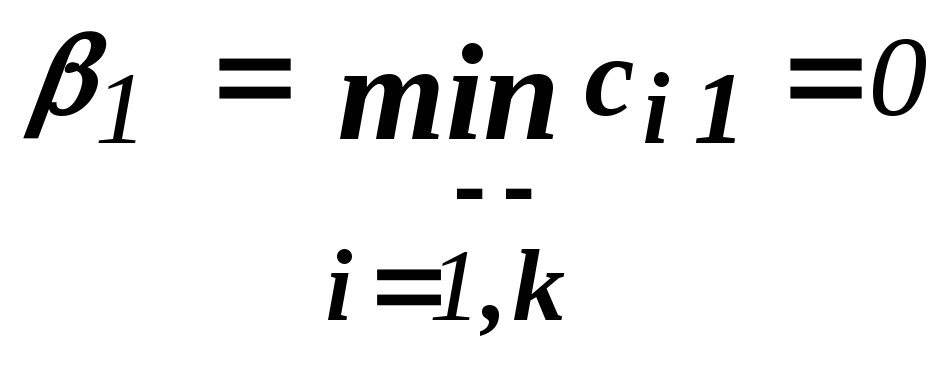
Далее:

Следовательно:

Прием 7. Определение весовых коэффициентов при одинаковом приоритете частных критериев.

В этом способе выбора весовых коэффициентов определяется по формуле:

критерии равноправны.