- •Задачи векторной оптимизации.
- •Основные понятия и определения.
- •Методы решения задач многокритериальной оптимизации.
- •Метод "обобщенного критерия".
- •Основные виды сверток.
- •Линейная свертка и ее свойства.
- •Методы определения весовых коэффициентов.
- •Решение задач векторной оптимизации при наличии дополнительной информации о важности частных критериев оптимальности.
- •Метод выделения главного критерия.
- •Метод последовательной оптимизации с учетом жесткого приоритета.
- •Метод последовательных уступок.
- •Метод равенства частных критериев.
- •Метод квазиравенства частных критериев оптимальности.
- •Метод гарантированного результата или метод минимакса.
- •Поиск оптимально - компромиссного решения в области компромиссов.
Задачи векторной оптимизации.
Основные понятия и определения.
Напомним, что классической задачей оптимизации или задачей математического программирования является следующая:
найти минимум функции
нескольких переменных
![]() при ограничениях
при ограничениях![]() ,
или обычно такая задача записывается
в векторной форме :
,
или обычно такая задача записывается
в векторной форме :
![]()
![]() (11.1.0 )
(11.1.0 )
![]() - векторная функция с
компонентами
- векторная функция с
компонентами
![]()
![]() - обычно называется
целевой функцией,
- обычно называется
целевой функцией,
![]() - векторная функция
ограничений.
- векторная функция
ограничений.
Множество
![]() называетсядопустимым
, то есть допустимое
множество – это части пространства
называетсядопустимым
, то есть допустимое
множество – это части пространства
![]() ,
где выполнены ограничения :
,
где выполнены ограничения :![]() .
.
Множество
![]() называетсяоптимальным
, если оно допустимо и кроме того, на
этом множестве
называетсяоптимальным
, если оно допустимо и кроме того, на
этом множестве
![]() принимает минимальное значение.
принимает минимальное значение.
Такую задачу еще можно
назвать задачей скалярной
оптимизации, так как
![]() -
скалярная функция переменной
-
скалярная функция переменной![]() .
Поскольку в дальнейшем нам придётся
на некоторых этапах обращаться к
решению задачи ( 11.1 .0 ), кратко напомним
основные моменты : задача ( 11.1 .0 ) может
не иметь решения, может иметь одно
решение, может иметь более одного
решения.
.
Поскольку в дальнейшем нам придётся
на некоторых этапах обращаться к
решению задачи ( 11.1 .0 ), кратко напомним
основные моменты : задача ( 11.1 .0 ) может
не иметь решения, может иметь одно
решение, может иметь более одного
решения.
Работы по скалярной оптимизации имеют два основных направления:
выявление условий единственности решения задачи ( 11.1 .0 ) , либо условий отсутствия решений;
разработка численных методов решения задачи ( 11.1 .0 ).
Эти два направления тесно связаны, так как разработка численных методов обычно предполагает выполненными определенные условия ,следующие из 1-го направления.
С другой стороны, существуют численные методы, которые в ходе своей реализации выявляют отсутствие решения или его не единственность.
Напомним, что основными численными методами решения задачи ( 11.1 .0 ) являются:
методы штрафных функций ;
прямые методы, использующие только значения функций;
градиентные методы ;
метод случайного поиска.
И, наконец, в заключение напоминания о задаче скалярной оптимизации, заметим, что в настоящее время существуют самые разнообразные пакеты прикладных программ, решающих задачу ( 11.1 .0 ) . Это пакеты на самых распространенных языках / FORTRAN, BASIC, PASCAL, C/ и для различных вычислительных машин /ЕС, СМ, ПЭВМ/.
Задача, решению которой посвящена данная работа, состоит в нахождении минимума векторной функции
![]() при
некоторых ограничениях и может быть
записана так :
при
некоторых ограничениях и может быть
записана так :
![]()
![]()
![]()
![]() (11.1.0 )
(11.1.0 )
![]() - компоненты векторной
функции
- компоненты векторной
функции
![]() ,
часто их называют частными критериями,
поэтому и задачу
( 1.2 ) называют
многокритериальной.
,
часто их называют частными критериями,
поэтому и задачу
( 1.2 ) называют
многокритериальной.
В задаче ( 11.1 .0 ) функцию мы называли целевой, поэтому задачу ( 11.1 .0 ) еще называют и задачей многоцелевой оптимизации. Заметим, что в общем случае, для реализации одной цели можно использовать много критериев. Поэтому задачу ( 11.1 .0 ) можно называть задачей многоцелевой оптимизации, предполагая, что одной цели соответствует один критерий.
Итак, мы будем заниматься задачей ( 11.1 .0 ), которая в разных источниках может называться как :
задача векторной оптимизации;
многокритериальная задача оптимизации;
задача многоцелевой оптимизации.
Дело в том, что реальные задачи , а особенно задачи , связанные с созданием АСУ, САПР, задачи системного анализа, теории больших систем и так далее, в основном многокритериальные, поэтому сама жизнь требует умения их решать, что подчеркивает актуальность проблемы.
В настоящее время существуют отдельные исследования как в теоретическом аспекте, так и в сфере создания алгоритмов.
Целью данной работы является попытка обобщения этих исследований, ориентированная в основном на практическое применение, то есть использование конкретных алгоритмов решения с минимальным их теоретическим обоснованием.
С математической точки
зрения, задача ( 11.1 .0 ) может иметь
решение
![]() только в том случае, если оно совпадает
со всеми решениями скалярных задач:
только в том случае, если оно совпадает
со всеми решениями скалярных задач:
![]()
![]()
Однако, этот вариант, как правило не представляет интереса для практических задач, поскольку в реальных задачах уменьшение одного критерия приводит часто к увеличению другого и возникает проблема сравнимости критериев.
Действительно, какое
решение /
![]() или
или![]() / лучше, например, для двухкритериальной
задачи :
/ лучше, например, для двухкритериальной
задачи :
 ,
,
 ;
; ,
,
 .
.
По-видимому, в данном случае, решения несравнимы.
В дальнейшем будем использовать следующие понятия и определения.
Назовем область
![]()
![]() -допустимой
областью, а
-допустимой
областью, а
![]() -допустимой
точкой.
-допустимой
точкой.
![]() -
область, где выполнены все ограничения.
Критерии
-
область, где выполнены все ограничения.
Критерии![]() называютупорядоченными
по важности, если
каждый
называютупорядоченными
по важности, если
каждый
предыдущий критерий
важнее всех последующих , то есть
![]() - самый важный, следующий за ним
- самый важный, следующий за ним![]() и так далее.
и так далее.
Определение 1.
Из двух точек
![]() точка
точка![]() называетсядоминирующей
по отношению к
называетсядоминирующей
по отношению к
![]() (
(![]() ),
если для всех
),
если для всех![]() выполняется
выполняется![]() и, кроме того , по крайней мере для одного
и, кроме того , по крайней мере для одного![]() :
:![]() .
.
Определение 2.
Точка
![]() называетсяулучшаемой,
если существует хотя бы одна точка
называетсяулучшаемой,
если существует хотя бы одна точка
![]() ,
такая, что
,
такая, что![]() ,
,
![]() и хотя бы для одного
и хотя бы для одного
![]() :
:![]() ,
в противном случае точка
,
в противном случае точка![]() не
улучшаемая или эффективная.
не
улучшаемая или эффективная.
Определение 3.
Множество
![]() ,
состоящее из эффективных точек называетсямножеством
решений, оптимальных по Парето.
,
состоящее из эффективных точек называетсямножеством
решений, оптимальных по Парето.
( В. Парето / 1848-1923 / - итальянский экономист, социолог, математик. Впервые ввел понятие " эффективная точка множества ". )
Множество
![]() является решением задачи ( 11.1 .0 ), с
формальной точки зрения этим можно
завершить рассмотрение задачи ( 11.1 .0 )
. Множество
является решением задачи ( 11.1 .0 ), с
формальной точки зрения этим можно
завершить рассмотрение задачи ( 11.1 .0 )
. Множество![]() строится затем, чтобы из него, привлекая
неформальные критерии можно было бы
выбрать некоторое решение. Однако обычно
выбор делается в пространстве критериев,
а затем в силу взаимно-однозначного
соответствия выбирается элемент из
строится затем, чтобы из него, привлекая
неформальные критерии можно было бы
выбрать некоторое решение. Однако обычно
выбор делается в пространстве критериев,
а затем в силу взаимно-однозначного
соответствия выбирается элемент из![]() .
В задаче ( 11.1 .0 )
.
В задаче ( 11.1 .0 )
![]() задает отображение области
задает отображение области![]() в некоторую область
в некоторую область![]() .
.![]() называетсяобластью
критериев.
называетсяобластью
критериев.
Определение 1.
Доминирование остается
в силе и для точек из
![]() .
.![]() - элемент
- элемент![]() .
Область
.
Область![]() называетсяобластью
согласия, если
из любых двух точек этой области одна
будет доминирующей по отношению к
другой. Если
называетсяобластью
согласия, если
из любых двух точек этой области одна
будет доминирующей по отношению к
другой. Если
![]() совпадает с
совпадает с![]() ,
тогда существует единственная точка
,
тогда существует единственная точка![]() ,
являющаяся доминирующей по отношению
ко всем другим точкам из
,
являющаяся доминирующей по отношению
ко всем другим точкам из![]() , то есть
, то есть![]() - оптимальное решение задачи
( 11.1 .0 ) .
- оптимальное решение задачи
( 11.1 .0 ) .
Определение 2.
Точка
![]() называется неулучшаемой,
если не существует ни одной точки из
называется неулучшаемой,
если не существует ни одной точки из
![]() ,
компоненты которой были бы не более
компонент неулучшаемой точки / хотя
бы по одной компоненте необходимо
выполнение строгого неравенства /.
Область
,
компоненты которой были бы не более
компонент неулучшаемой точки / хотя
бы по одной компоненте необходимо
выполнение строгого неравенства /.
Область![]() ,
вложенная либо равная
,
вложенная либо равная![]() называетсяобластью
неулучшаемых точек.
называетсяобластью
неулучшаемых точек.
Давайте рассмотрим следующую задачу :
![]()
![]()
![]() (11.1.0 )
(11.1.0 )
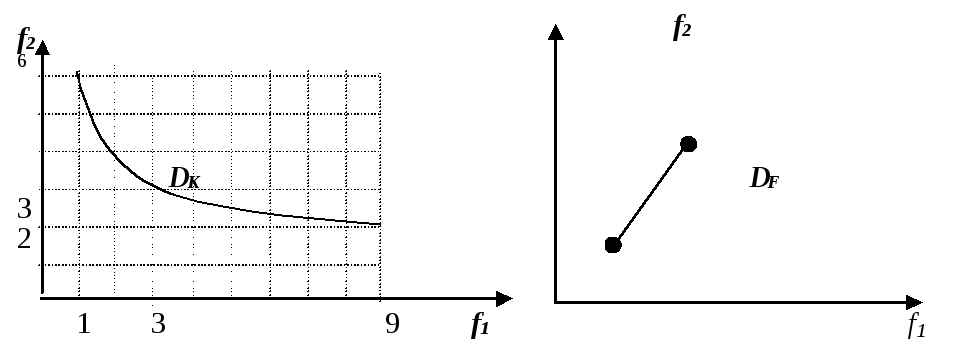
Графически она представлена следующем рисунке
Рисунок 11‑1
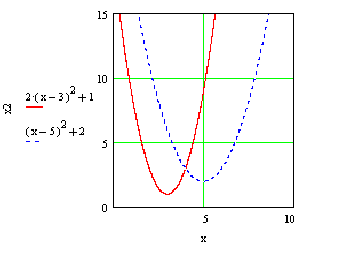
![]() , а также для
, а также для![]() оба критерия возрастают, следовательно
точки из полуинтервала
оба критерия возрастают, следовательно
точки из полуинтервала![]() и
и![]() улучшаемы : для
улучшаемы : для![]() точка
точка![]() дает
меньшее значение критериев, аналогично
ведет себя
дает
меньшее значение критериев, аналогично
ведет себя![]() для
для![]() .
.
Мы видим, что внутри
отрезка
![]() до точки пересечения графиков обеих
функций, т.е. на отрезке
до точки пересечения графиков обеих
функций, т.е. на отрезке![]()
![]() убывает, а
убывает, а![]() возрастает, на отрезке
возрастает, на отрезке![]() наоборот:
наоборот:![]() возрастает, а
возрастает, а![]() убывает, следовательно, согласно
введенным выше определениям - отрезок
убывает, следовательно, согласно
введенным выше определениям - отрезок![]() для данной задачи является множеством
решений, оптимальных по Парето.
для данной задачи является множеством
решений, оптимальных по Парето.
На следующем рисунке
в пространстве
![]() , для этой же задачи представлены
области согласия и компромиссов,
являющиеся плоскими кривыми, полученными
в результате отображения области
, для этой же задачи представлены
области согласия и компромиссов,
являющиеся плоскими кривыми, полученными
в результате отображения области![]() / отрезок
/ отрезок![]() / в области
/ в области![]() .
.
Такое представление
является наглядным пособием и удобным
для того, кому предстоит сделать выбор
элемента из
![]() .
С увеличением числа частных критериев
оптимальности наглядность теряется.
.
С увеличением числа частных критериев
оптимальности наглядность теряется.
|
x |
f1(x) |
f2(x) |
|
3 |
1 |
6 |
|
4 |
3 |
3 |
|
5 |
9 |
2 |
Р