
- •Методы одномерной минимизации.
- •Основные понятия
- •Постановка задачи.
- •Классический подход.
- •Методы решения задачи минимизации для унимодальных функций.
- •Понятие унимодальной функции.
- •Общие сведения о численных методах оптимизации, их классификация.
- •Порядок метода.
- •Сходимость метода.
- •Критерии останова.
- •Методы минимизации 0-го порядка.
- •Метод дихотомии.
- •Метод Фибоначчи.
- •Метод золотого сечения.
- •X1 x2
- •Метод квадратичной интерполяции (парабол).
- •Метод Ньютона.
- •Численные методы минимизации многоэкстремальных функций.
- •Метод перебора.
- •Метод ломаных.
Методы одномерной минимизации.
Основные понятия
Постановка задачи.
![]() - числовая функция
вещественной переменной
- числовая функция
вещественной переменной
![]() .
Под задачей одномерной минимизации на
отрезке
.
Под задачей одномерной минимизации на
отрезке![]() понимается поиск
понимается поиск![]() такого, что
такого, что
![]() (3.1.0 )
(3.1.0 )
![]() - наименьшее
значение
- наименьшее
значение
![]() на
на
![]() ;
;
![]() ,
удовлетворяющее ( 3.1 .0 ) называется
точкой минимума
,
удовлетворяющее ( 3.1 .0 ) называется
точкой минимума
![]() на
на
![]() ;
;
![]() -
множество точек минимума на
-
множество точек минимума на
![]() ;
;
![]() может быть пустым,
содержать конечное или бесконечное
число точек.
может быть пустым,
содержать конечное или бесконечное
число точек.
Замечание.
Задача поиска максимума
![]() сводится к задаче поиска минимума
сводится к задаче поиска минимума
![]() :
:
![]()
Задача одномерной минимизации состоит из двух частей:
локализации точек минимума, то есть указания отрезков, содержащих единственную точку минимума;
поиска точки минимума на заданном отрезке при наличии информации о том, что на этом отрезке заведомо существует единственный минимум.
Задача локализации минимума обычно решается с помощью классического метода, основанного на дифференциальном исчислении.
Кроме того, существуют и некоторые вычислительные процедуры, позволяющие в определенных условиях такую задачу решать.
В основном, ниже рассматриваются численные методы, позволяющие решать локализованные задачи.
Классический подход.
Напомним 2 важные для данного рассмотрения теоремы из классического анализа.
Теорема Вейерштрасса.
Если
![]() непрерывна на
непрерывна на
![]() ,
то
,
то
![]() существует.
существует.
Теорема Ферма.
Пусть![]() дифференцируема в точке
дифференцируема в точке
![]() . Если
. Если
![]() доставляет
локальный минимум
доставляет
локальный минимум
![]() ,
то
,
то
![]()
Определение.
![]() называется
точкой локального
минимума, если
существует
> 0 такое, что
для
называется
точкой локального
минимума, если
существует
> 0 такое, что
для
![]() выполняется
выполняется
![]()
Пусть
![]() кусочно-непрерывная
и кусочно-гладкая на
кусочно-непрерывная
и кусочно-гладкая на
![]() функция. Это означает, что на
функция. Это означает, что на![]() может существовать лишь конечное число
точек, где
может существовать лишь конечное число
точек, где
![]() терпит
разрыв I-го
рода, либо
терпит
разрыв I-го
рода, либо
![]() непрерывна, но не имеет производной.
непрерывна, но не имеет производной.
Тогда точками минимума могут быть такие точки, в которых:
-
![]() терпит разрыв;
терпит разрыв;
-
![]() непрерывна, но
непрерывна, но![]() не существует;
не существует;
-
![]()
- либо
![]() ,
либо
,
либо![]() .
.
Рисунки ниже иллюстрируют эти 4 случая.

Рисунок 3.2.1
![]() терпит
разрыв в точке
терпит
разрыв в точке
![]() .
.

Рисунок 3.2.2
![]() непрерывна,
но производной не существует.
непрерывна,
но производной не существует.

Рисунок 3.2.3
![]() .
.

Рисунок 3.2.4
![]() .
.
Методы решения задачи минимизации для унимодальных функций.
Понятие унимодальной функции.
Определение.
![]() унимодальна на
унимодальна на
![]() ,
если существуют
,
если существуют
![]() такие, что
такие, что
 строго монотонно
убывает на
строго монотонно
убывает на
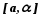 ,
, строго
монотонно возрастает на
строго
монотонно возрастает на ,
,для

Если
![]() ,то
,то
![]() строго унимодальна.
строго унимодальна.
Унимодальная функция не обязательно должна быть непрерывной и дифференцируемой. Ниже представлены примеры унимодальных функций.

Рисунок 3.3.5
Строго унимодальная, непрерывная, дифференцируемая функция.

Рисунок 3.3.6
Нестрого унимодальная, непрерывная, дифференцируемая функция.
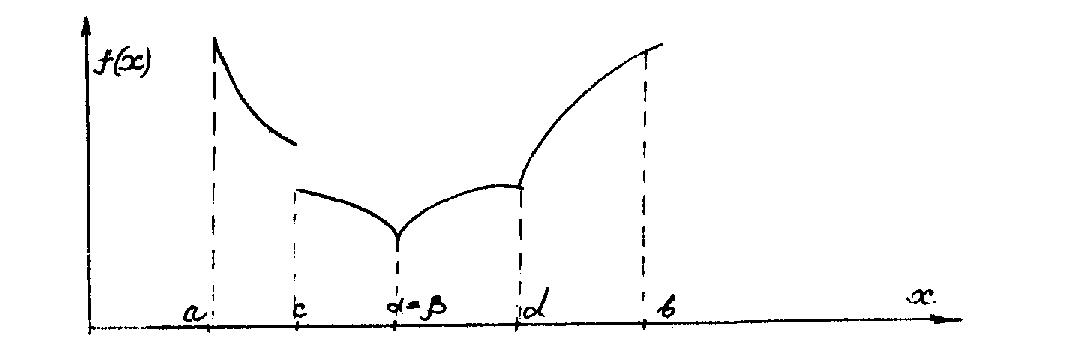
Рисунок 3.3.7
При
![]() имеет разрывI- го рода,
при
имеет разрывI- го рода,
при
![]() ,
,
![]() производной у
производной у![]() не существует.
не существует.
Общие сведения о численных методах оптимизации, их классификация.
Определение 1.
Под численным методом одномерной
минимизации понимается процедура
получения числовой последовательности
![]() приближений
к точному решению задачи минимизации.
приближений
к точному решению задачи минимизации.
Определение 2. Под численным методом одномерной минимизации понимается процедура получения вложенных отрезков, покрывающих точное решение:
![]()
![]() .
.
Порядок метода.
Метод имеет порядок
k,
если он использует информацию о
производных
![]() до
k
- порядка включительно. Обычно применяются
методы 0-го, 1-го и 2-го порядков.
до
k
- порядка включительно. Обычно применяются
методы 0-го, 1-го и 2-го порядков.
Сходимость метода.
Численный метод
сходится, если последовательность
![]() сходится к
точному решению, то есть
сходится к
точному решению, то есть
![]() (скорость
сходимости характеризуется
(скорость
сходимости характеризуется
![]() )
или метод сходится, если
)
или метод сходится, если
![]() ;
;
![]() (скорость сходимости характеризуется
разностью
(скорость сходимости характеризуется
разностью
![]() ).
).
