4. Метод Ньютона.

Метод Ньютона относится к методам 2-го порядка и рекомендуется с применению в том случае, когда задача минимизации достаточно хорошо локализована.

Обычно это имеет место в том случае, когда на начальном этапе применяется один из методов 0-го порядка, а затем осуществляется переход к методу Ньютона. Для этого необходимым условием является гладкость , существование не равных нулю , , для .

Тогда если -k-е приближение к точке минимума, то расчетной формулой метода Ньютона будет формула

.

Метод Ньютона имеет высокую скорость сходимости:

где - точка минимума;С - некоторая положительная константа.

Процесс вычисления продолжается до тех пор, пока не будет достигнуто

На следующем рисунке приведена блок-схема алгоритма.

Рисунок 3.3.14

Блок - схема метода Ньютона.

Пример.

Найти минимум на отрезке c точностью.

Зададимся , например, возьмем середину отрезка :

Пусть

Для данного примера расчетной формулой метода Ньютона будет

1-й шаг.

2й шаг.

Решение.

Замечание.

Число сохраняемых знаков после округления определяется заданной точностью .

4. Численные методы минимизации многоэкстремальных функций.

До сих пор рассматривались унимодальные функции, имеющие на отрезке единственную точку минимума. Если функция на отрезке многоэкстремальна (то есть существует несколько минимумов функции ), то возникает задача отыскания глобального минимума функции .

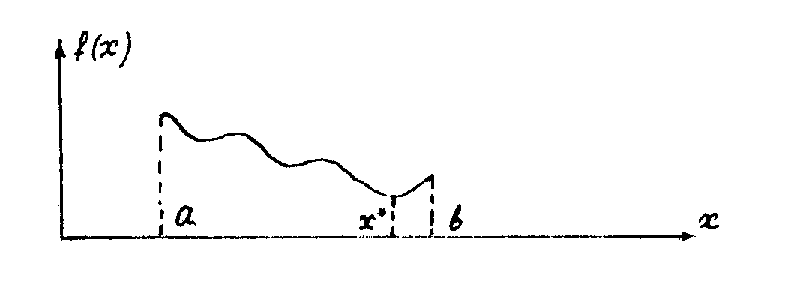
Рисунок 3.4.15

Рисунок 3.4 .15 - пример такой функции, где - точка глобального минимума.

Ограничимся рассмотрением функций, удовлетворяющих условию Липшица на отрезке :

,

где M - константа Липшица.

Существует несколько методов определения глобального минимума таких функций. Остановимся на двух из них: методе перебора и методе ломаных.

1. Метод перебора.

Суть метода перебора состоит в следующем:

в точках отрезка

,

вычисляются значения функции и в качестве минимального значения принимается значение

.

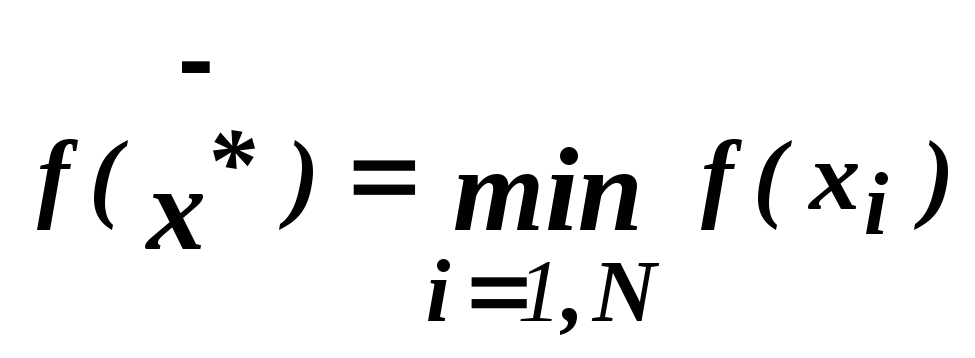Погрешность метода не превосходит величины. Это легко показать, так как если точка глобального минимума, то очевидно, найдется такая точка ,, что

Тогда с учетом условия Липшица

Таким образом, задаваясь необходимой величиной погрешности можно определить требуемое количество точекна отрезке :

Блок-схема метода перебора приведена ниже.

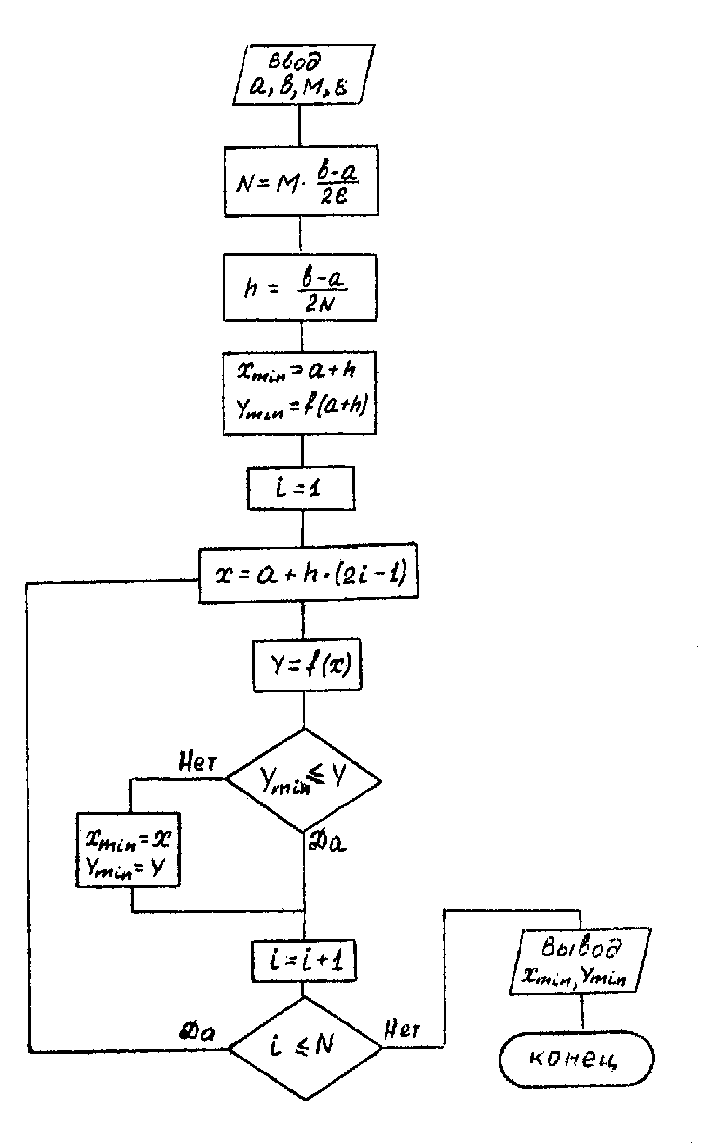
Рисунок 3.4.16

2. Метод ломаных.

На отрезке выбирают точек

В каждой точке вычисляется значение функции и строится миноранта

для функции, представляющая собой ломаную:

определяется точка x, в которой достигает минимума, и она принимается в качестве дополнительнойточки для исследования функции на минимум

.

С введением точки минорантапреобразуется в минорантуи далее процесс введения следующей точки повторяется.

В качестве приближения к искомому значению минимума после вычислений значений функции принимается величина

.

Очевидно, что погрешность метода не превосходит величины

- .

Значение может быть задано или же будет определяться, исходя из требуемой точностивычисления значения минимума функции . Во втором случае вычисления прекращаются как только

-

Рисунок 3.4 .17 - Рисунок 3.4 .20 иллюстрируют применение метода ломаных для определения глобального минимума функции . Проведено четыре итерации.

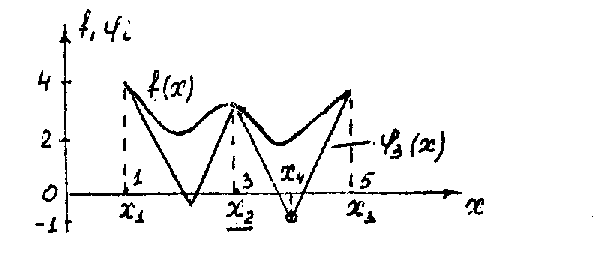
Рисунок 3.4.17

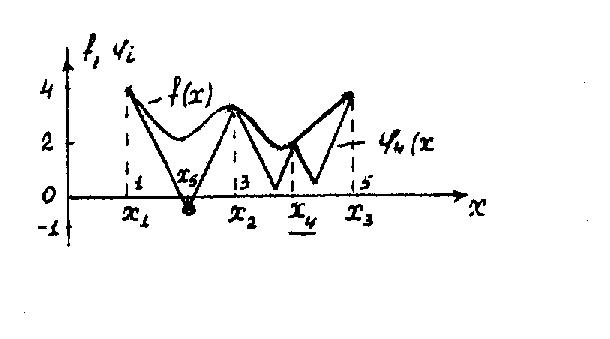
Рисунок 3.4.18

Рисунок 3.4.19

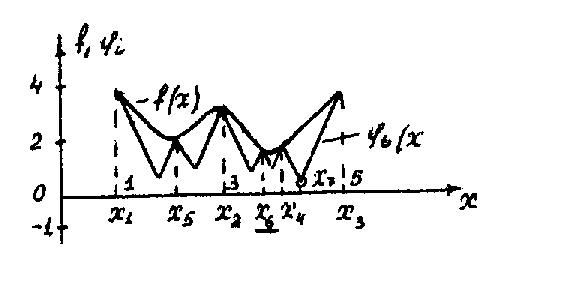
Рисунок 3.4.20

При реализации обоих методов требуется знать значение константы Липшица . На практике значение часто неизвестно. В этом случае в качестве можно использовать оценку

,

где

,