125

12. Оптимальное управление.

    1. Определение оптимального программирования.

В общем виде задачи оптимального управления могут быть сформулированы следующим образом:

определить вектор-функции при, доставляющие минимум функционалу

(12.1.0)

при описании движения

(12.1.0 )

при ограничениях вдоль траектории

(12.1.0)

и краевых условиях

, (12.1.0)

где – непрерывные и дифференцируемые функции по совокупности ,

,

- некоторые многообразия в .

Напоминание.

Будем говорить, что на множестве задан функционал, если известно правило, которое каждому элементуставит в соответствие определенное число. Можно сказать, что функция осуществляет отображение множества(имеющего произвольную природу) на множество действительных чисел.

Пример 1:

Рассмотрим множество областей, представляющих собой фигуры, ограниченные замкнутыми кривыми. Каждой областисоответствует действительное число, равное ее площади.

Пример 2:

Рассмотрим множество функций, заданных и непрерывных на отрезке . Элемент множества- это сама функцияи ему соответствует число, равное значению функции.

- функционал.

В зависимости от конкретного вида выражений задачи оптимального управления можно разбить на три группы. В каждой из групп определяющей характеристикой являются способы, с помощью которых задаются:

1. функционал;

2. ограничения вдоль траектории;

3. краевые условия.

1. Способы задания функционала.

1. Интегральный функционал.

Задача Лагранжа.

(12.1.0)

где – дифференцируемая функция по своим переменным.

В случае отсутствия ( 12.1 .0) , то есть задача [( 12.1 .0), ( 12.1 .0 ),( 12.1 .0)] называется задачей Лагранжа.

2. Задача Майера.

(12.1.0)

при ограничениях ( 12.1 .0 ), ( 12.1 .0),( 12.1 .0)

Формально задача Майера является более общей, чем задача Лагранжа. Любая задача Лагранжа может быть сведена к задаче Майера.

3. Задача Больца.

Функционал смешанного типа:

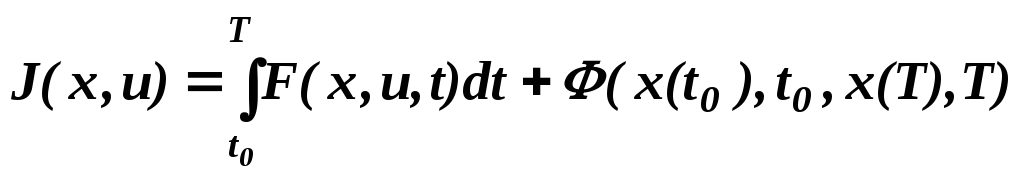(12.1.0)

То есть нужно определить векторы , доставляющие минимум функционалу ( 12.1 .0) при ограничениях

( 12.1 .0 ), ( 12.1 .0),( 12.1 .0).

4. Задача на быстродействие.

Этим термином объединяются задачи, в которых функционалом является время

(12.1.0)

1. Способы задания ограничения .

1. Ограничение на управление.

,

где - некоторое замкнутое множество из.

В частном случае может быть, к примеру, .

2. Ограничения на фазовые переменные.

.

Ограничения могут быть в виде равенств:

,

и в виде неравенств:

.

3. Совместные ограничения на управление и фазовые переменные.

Когда ограничения на не могут быть разделены.

Подобные задачи часто встречаются в экономике:

в виде равенств:

,

и неравенств:

.

4. Изопериметрическая задача (задача с интегральными ограничениями).

Определить минимум функционала ( 12.1 .0) при следующих ограничениях:

,

где - некоторые скалярные функции, а- заданные числа.

Формулировка этой задачи:

определить кривую данной длины, которая ограничивает максимальную площадь.

Класс изопериметрических задач играет большую роль как в технике, так и в экономике, когда задан суммарный объем некоторого ресурса, которым мы вправе распоряжаться (например, в технике: запас горючего для самолета).

Изопериметрическая задача может быть сведена к задаче Лагранжа увеличением размерности вектора на(то есть станет).

Например:

,

должны удовлетворять условиям.

Пример.

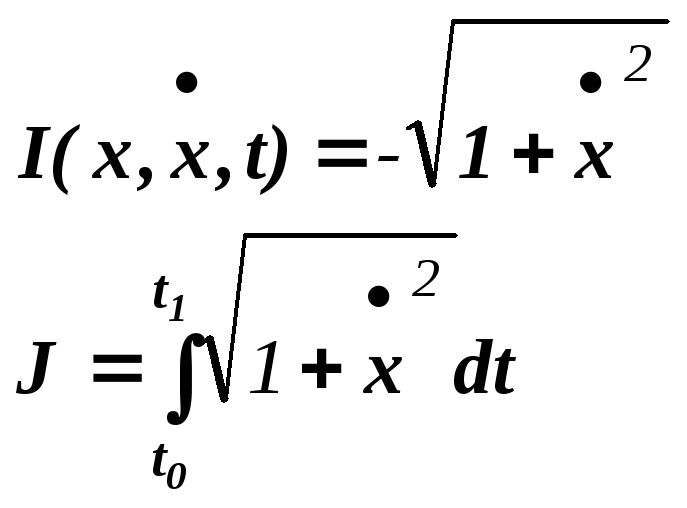
Уравнение Эйлера:

Отсюда

- является ,

,

определяются из граничных условий:

, .