
- •Электроизмерительные приборы. Классификация электроизмерительных приборов
- •Условные обозначения, наносимые на электроизмерительные приборы
- •Определение абсолютной и относительной погрешности измерений с применением электроизмерительных приборов
- •2. Порядок выполнения работы
- •3. Техника безопасности
- •4. Контрольные вопросы
- •Расширение пределов измерения приборов. Шунты и дополнительные сопротивления
- •Порядок выполнения работы
- •3. Техника безопасности
- •Контрольные вопросы
- •Лабораторная работа №3 Исследование электростатического поля
- •Основные характеристики электростатического поля
- •Метод моделирования
- •Установка для исследования электростатического поля с помощью осциллографа и звукового генератора
- •4 Порядок выполнения работы
- •5 Техника безопасности
- •Контрольные вопросы
- •Лабораторная работа №4 Градуировка электростатического вольтметра
- •Теория метода и описание измерительной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Техника безопасности
- •Контрольные вопросы
- •Лабораторная работа №5 Определение электроемкости конденсаторов
- •1 Основные понятия и закономерности
- •1.1Понятие электроемкости. Электроемкость уединенного проводника
- •1.2 Электроемкость системы проводников. Конденсаторы
- •Энергия заряженного проводника. Энергия конденсатора
- •1.4. Последовательное и параллельное соединение конденсаторов
- •2 Теория метода измерения электроемкости конденсатора и описание схемы установки
- •Порядок выполнения работы
- •Баллистический гальванометр
- •5 Техника безопасности
- •Контрольные вопросы
- •Лабораторная работа №6 Измерение омических сопротивлений с помощью амперметра и вольтметра
- •1 Основные понятия и закономерности
- •2 Теория метода измерения сопротивлений с помощью амперметра и вольтметра и описание измерительных установок
- •3 Порядок выполнения работы и обработка результатов измерений
- •4 Правила пользования много предельными приборами
- •Контрольные вопросы
- •Техника безопасности
- •Лабораторная работа №7 Измерение сопротивлений проводников методом мостиковой схемы
- •Основные формулы и законы
- •Вывод рабочей формулы
- •Последовательное и параллельное соединение проводников
- •2. Порядок выполнения работы и обработка результатов измерений
- •Техника безопасности
- •Контрольные вопросы
- •Лабораторная работа №8 Измерение электродвижущей силы (эдс) источника тока методом компенсации
- •Основные понятия и законы
- •Методы измерения электродвижущей силы источника тока (эдс)
- •Устройство нормального элемента
- •Техника безопасности
- •Контрольные вопросы
- •Лабораторная работа №9 Исследование электрической цепи постоянного тока
- •Основные понятия и законы
- •Порядок выполнения работы
- •3. Техника безопасности
- •4. Контрольные вопросы
- •Лабораторная работа №10 Изучение процессов заряда и разряда конденсатора и определение его электроемкости
- •Основные понятия и законы
- •Установившийся и переходный режим электрической цепи
- •Заряд конденсатора через активное сопротивление (резистор)
- •Разряд конденсатора
- •Свойства экспоненциальной функции. Постоянная времени цепи. Определение электроемкости конденсатора
- •Описание установки и порядок выполнения работы
- •3. Техника безопасности
- •Контрольные вопросы
- •Лабораторная работа №11 Измерение термоэдс с помощью потенциометра
- •Основные понятия и закономерности
- •Описание установки и порядок выполнения работы
- •Устройство и принцип работы потенциометра
- •Подготовка потенциометра к измерениям и измерение термо – эдс
- •2.3. Порядок выполнения работы
- •Техника безопасности
- •Контрольные вопросы
- •Лабораторная работа №12 Определение работы выхода электрона из металла по вольт-амперным характеристикам электронной лампы
- •Основные понятия и закономерности
- •Методика исследования и описание установки
- •Порядок выполнения работы
- •Техника безопасности
- •5. Контрольные вопросы
- •Лабораторная работа №13 Определение работы выхода электрона из металла методом компенсации охлаждения нити
- •Основные понятия и закономерности
- •Описание установки и методика измерений
- •Порядок выполнения работы
- •Техника безопасности
- •Контрольные вопросы
- •Литература
3. Техника безопасности
Включение установки производится только после проверки ее преподавателем или лаборантом.
Во время работы запрещается касаться токоведущих частей установки.
По окончании работы уменьшить напряжение на выпрямителе до нуля и отключить источник питания от электрической сети.
Контрольные вопросы
Какие приборы используются для измерения силы тока в цепи? Как их включают в цепь?
Изобразить схему включения амперметра для измерения силы тока.
Как увеличить предел измерения амперметра?
Как подключить шунт к прибору? Изобразить схему включения шунта.
Выведите формулу для расчета сопротивления шунта.
Какие приборы используются для измерения напряжения?
Изобразить схему включения вольтметра для измерения напряжения на некотором сопротивлении.
Как увеличить предел измерения вольтметра?
Вывести формулу для расчета дополнительного сопротивления.
Изобразите схему включения дополнительного сопротивления.
Как изменяется цена деления шкалы при увеличении пределов измерения электроизмерительных приборов?
Как изменяется чувствительность электроизмерительных приборов при увеличении пределов измерения?
Лабораторная работа №3 Исследование электростатического поля
Цель работы:
Изучить характеристики электростатического поля;
Изучить графическое изображение электростатических полей;
Измерить распределение потенциалов электростатических полей различных систем зарядов;
Построить линии напряженности электростатических полей различных систем зарядов.
Основные характеристики электростатического поля
Любой неподвижный электрический заряд создает в пространстве электростатическое поле. Электростатическое поле является одной из форм существования материи, особенность которой состоит в том, что электростатическое поле действует с некоторой силой на электрический заряд, помещенный в любую точку поля. Отсюда следует, что обнаружить и исследовать электростатическое поле можно только с помощью электрического заряда. Такой заряд – прибор для изучения электростатического поля называется пробным электрическим зарядом или просто пробным зарядом. Пробный заряд должен быть настолько мал, чтобы своим полем не искажать изучаемое поле. Так как пробный заряд является измерительным прибором для электростатического поля, то его характеристики не зависят от величины пробного заряда.
Начало количественного изучения электрических явлений было положено Кулоном, который в 1785 году установил на опыте закон взаимодействия электрических зарядов. Он установил закон взаимодействия точечных зарядов. Под точечным зарядом понимается заряженное тело, размеры которого значительно меньше расстояний до других зарядов, в том числе и до пробного заряда. Согласно закону Кулона, величина силы взаимодействия двух точечных зарядов определяется формулой:
 (1)
(1)
Здесь
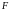 - величина силы взаимодействия зарядов;
- величина силы взаимодействия зарядов;
 - модули величин взаимодействующих
зарядов;
- модули величин взаимодействующих
зарядов;
 - расстояние между зарядами;
- постоянная электростатического
взаимодействия;
- расстояние между зарядами;
- постоянная электростатического
взаимодействия;
 - электростатическая постоянная вакуума.
Значение постоянной электростатического
взаимодействия
зависит от выбора системы единиц. В
системе единиц СИ значение постоянной
электростатического взаимодействия
равно силе, с которой взаимодействуют
два точечных заряда величиной по одному
кулону, находящиеся на расстоянии 1 м
друг от друга. На опытах с крутильными
весами измерено значение этой величины
и получено, что
- электростатическая постоянная вакуума.
Значение постоянной электростатического
взаимодействия
зависит от выбора системы единиц. В
системе единиц СИ значение постоянной
электростатического взаимодействия
равно силе, с которой взаимодействуют
два точечных заряда величиной по одному
кулону, находящиеся на расстоянии 1 м
друг от друга. На опытах с крутильными
весами измерено значение этой величины
и получено, что
 .
Дальнейшие исследования электромагнитных
явлений показали, что эту величину можно
и удобнее выразить через величину
- электростатическую постоянную вакуума.
При этом было измерено значение данной
величины
.
Дальнейшие исследования электромагнитных
явлений показали, что эту величину можно
и удобнее выразить через величину
- электростатическую постоянную вакуума.
При этом было измерено значение данной
величины
 .
Из формулы (1) видно, что связь между
величинами
и
определяется выражением
.
Из формулы (1) видно, что связь между
величинами
и
определяется выражением
 (2).
(2).
При
изучении взаимодействия точечных
зарядов нужно учесть, что формула (1)
справедлива в случае, если заряды
взаимодействуют в вакууме или в воздухе.
Если же взаимодействие зарядов происходит
в некотором веществе, например в масле
или в какой-нибудь другой жидкости, то
необходимо учитывать, что любое вещество
уменьшает силу взаимодействия зарядов.
Для того, чтобы учесть влияние среды, в
которой происходит взаимодействие
зарядов, вводится понятие диэлектрической
проницаемости среды
 .
Диэлектрическая проницаемость среды
показывает, во сколько раз сила
взаимодействия зарядов в некоторой
среде меньше, чем сила взаимодействия
этих зарядов в вакууме. Диэлектрическая
проницаемость различных веществ
измеряется опытным путем и заносится
в таблицы и справочники. С учетом наличия
среды, в которой происходит взаимодействие
зарядов, закон Кулона будет иметь вид:
.
Диэлектрическая проницаемость среды
показывает, во сколько раз сила
взаимодействия зарядов в некоторой
среде меньше, чем сила взаимодействия
этих зарядов в вакууме. Диэлектрическая
проницаемость различных веществ
измеряется опытным путем и заносится
в таблицы и справочники. С учетом наличия
среды, в которой происходит взаимодействие
зарядов, закон Кулона будет иметь вид:
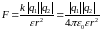 (3)
(3)
В настоящее время известно, что сила – величина векторная. Чтобы определить вектор силы взаимодействия зарядов, выберем систему отсчета, в которую поместим взаимодействующие заряды (Рис. 1).

Рис. 1
На
рисунке 1 отрицательный по знаку заряд
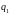 ,
помещенный в точку A,
взаимодействует с положительным по
знаку зарядом
,
помещенный в точку A,
взаимодействует с положительным по
знаку зарядом
 ,
помещенным в точку B.
,
помещенным в точку B.
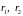 - радиус векторы этих зарядов в системе
координат XOY.
Для простоты выбрана двумерная система
координат, аналогичный рисунок можно
получить и в трехмерной системе координат.
- радиус векторы этих зарядов в системе
координат XOY.
Для простоты выбрана двумерная система
координат, аналогичный рисунок можно
получить и в трехмерной системе координат.
 - сила, с которой второй заряд действует
на первый заряд. Как видно, эта сила
направлена вдоль вектора
- сила, с которой второй заряд действует
на первый заряд. Как видно, эта сила
направлена вдоль вектора
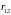 ,
который соединяет заряды. Тогда в
векторном виде закон Кулона можно
записать в виде:
,
который соединяет заряды. Тогда в
векторном виде закон Кулона можно
записать в виде:
 .
(4)
.
(4)
Согласно третьему закону Ньютона, сила, действующая на второй заряд со стороны первого заряда, будет такой же по величине, но противоположной по направлению.
Силу взаимодействия зарядов нельзя использовать для характеристики электростатического поля, так как она зависит от величин взаимодействующих зарядов. Поэтому для характеристики различных точек электростатического поля вводится понятие напряженности электростатического поля. При этом один из зарядов рассматривается как создающий электростатическое поле, а другой заряд играет роль прибора, изучающего поле – пробный заряд. Тогда можно дать следующее определение напряженности электростатического поля.
Напряженностью некоторой точки электростатического поля называется векторная физическая величина, равная отношению силы, действующей на пробный заряд, помещенный в изучаемую точку поля, к величине этого заряда. Пробный заряд имеет положительный заряд.
 (5)
(5)
Из определения напряженности следует, что напряженность в некоторой точке электростатического поля показывает, какая сила действует на единичный положительный заряд, помещенный в эту точку поля. Напряженность электростатического поля зависит от величины заряда, создающего поле, от положения изучаемой точки поля и от диэлектрической проницаемости среды, в которой создается поле. Напряженность электростатического поля не зависит от величины пробного заряда.
В
системе единиц СИ напряженность
электростатического поля измеряется
в
 (ньютон на кулон) или
(ньютон на кулон) или
 (воль на метр). Напряженность
электростатического поля не измеряется
прибором непосредственно. Она вычисляется
по результатам измерения потенциала.
(воль на метр). Напряженность
электростатического поля не измеряется
прибором непосредственно. Она вычисляется
по результатам измерения потенциала.
Используя определение напряженности и закон Кулона, можно получить формулу для вычисления напряженности поля точечного заряда в точке, находящейся на расстоянии от заряда:
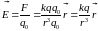 или
или
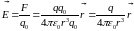 (6)
(6)
Формулы (6) записаны для напряженности электростатического поля в вакууме. Если электростатическое поле создано зарядом в некотором веществе с диэлектрической проницаемостью , то получим аналогичные формулы:
 или
или
 (7)
(7)
В
формулах (6) и (7)
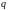 - точечный заряд, создающий поле, а
- точечный заряд, создающий поле, а
 - пробный заряд. Формулы (6) и (7) позволяют
определить направление вектора
напряженности электростатического
поля. Пусть
- точечный заряд, создающий поле имеет
положительный заряд. Выберем этот заряд
за начало системы отсчета и изобразим
напряженность поля в некоторой точке
A,
радиус-вектор которой относительно
этого заряда равен
- пробный заряд. Формулы (6) и (7) позволяют
определить направление вектора
напряженности электростатического
поля. Пусть
- точечный заряд, создающий поле имеет
положительный заряд. Выберем этот заряд
за начало системы отсчета и изобразим
напряженность поля в некоторой точке
A,
радиус-вектор которой относительно
этого заряда равен
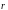 (Рис. 2).
(Рис. 2).

Рис. 2
Если точечный заряд, создающий поле , имеет отрицательный заряд, тогда напряженность поля будет направлена к заряду (Рис. 3).

Рис. 3
Формулы
(6) и (7) полностью соответствуют изображенным
рисункам, так как, если
 ,
то направление вектора напряженности
совпадает с направлением радиус-вектора
изучаемой точки, а если
,
то направление вектора напряженности
совпадает с направлением радиус-вектора
изучаемой точки, а если
 ,
то направление вектора напряженности
противоположно направлению радиус-вектора
изучаемой точки поля.
,
то направление вектора напряженности
противоположно направлению радиус-вектора
изучаемой точки поля.
Если
электростатическое поле создано системой
из нескольких зарядов
 ,
то при определении напряженности
используется принцип суперпозиции,
который включает следующие положения:
,
то при определении напряженности
используется принцип суперпозиции,
который включает следующие положения:
Каждый электрический заряд создает электрическое поле так, как будто других зарядов нет (принцип независимости электростатических полей)
Напряженность электростатического поля, созданного системой зарядов в некоторой точке поля, равна векторной сумме напряженностей, созданной отдельными зарядами:
 (8).
(8).
Здесь
 - напряженности полей, созданных
отдельными зарядами.
- напряженности полей, созданных
отдельными зарядами.
Электростатическое поле не действует на органы чувств человека. Поэтому для наглядного представления об электростатическом поле используется графическое изображение полей. Для графического изображения электростатических полей используются линии напряженности (более старое и менее точное понятие – силовые линии).
Линией напряженности электростатического поля называется линия, касательная в каждой точке которой, совпадает по направлению с вектором напряженности поля в этой точке. Таким образом, линия напряженности определяет в каждой точке, через которую она проходит, направление вектора напряженности, а, следовательно, и направление силы, действующей на положительный заряд, помещенный в эту точку. Густоту линий напряженности можно использовать для определения численного значения напряженности.
Закон Кулона справедлив только для точечных зарядов. Однако электростатические поля могут создаваться телами любой формы и любых размеров. Для определения напряженности таких полей нужно заряженное тело разбить на точечные заряды, применить закон Кулона к таким точечным зарядам, а затем провести процедуру интегрирования. Обобщением такой процедуры является теорема Остроградского – Гаусса, которая лежит в основе метода расчета напряженности полей, созданных телами любой формы и любого размера.
Основным
понятием теоремы Остроградского –
Гаусса является понятие потока вектора
напряженности через некоторую поверхность,
находящуюся в электростатическом поле.
Пусть известны линии напряженности
некоторого электростатического поля
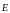 (Рис. 4), и задана площадка S,
которую пересекают линии напряженности.
(Рис. 4), и задана площадка S,
которую пересекают линии напряженности.
 - нормаль к площадке,
- нормаль к площадке,
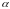 - угол между нормалью к площадке и
вектором напряженности.
- угол между нормалью к площадке и
вектором напряженности.

Рис. 4
Потоком вектора напряженности через площадку площадью S, расположенную в электростатическом поле так, что нормаль к площадке составляет угол с вектором напряженности, называется величина, определяемая формулой
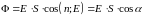 (9)
(9)
Формула
(9) используется, если в любой точке поля
напряженность поля имеет одинаковую
величину и направление. Такое
электростатическое поле называется
однородным полем. В случае, если
электростатическое поле неоднородное,
то необходимо определить поток вектора
напряженности через малую элементарную
площадку
 ,
для которой поле можно считать однородным,
а затем проинтегрировать по всему
пространству с учетом геометрии
заряженного тела, создающего поле. Поток
вектора напряженности через элементарную
площадку
определяется формулой:
,
для которой поле можно считать однородным,
а затем проинтегрировать по всему
пространству с учетом геометрии
заряженного тела, создающего поле. Поток
вектора напряженности через элементарную
площадку
определяется формулой:
 (10)
(10)
Поток вектора напряженности через некоторую поверхность получается путем интегрирования формулы (10):
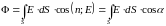 (11)
(11)
Аналогично, поток вектора напряженности через замкнутую поверхность определяется формулой:
 (12)
(12)
Теорема Остроградского – Гаусса формулируется следующим образом:
Поток
вектора напряженности электростатического
поля через произвольную замкнутую
поверхность, расположенную в этом поле,
равен алгебраической сумме зарядов,
находящихся внутри этой поверхности,
деленной на величину
для поля в вакууме или на величину
 для поля в некоторой среде с диэлектрической
проницаемостью
:
для поля в некоторой среде с диэлектрической
проницаемостью
:
 или
или
 (13)
(13)
Эта теорема наиболее удобна для расчета полей, которые созданы заряженными телами, обладающими симметрией. При расчете таких полей можно выбирать замкнутую поверхность с учетом симметрии заряженного тела, что значительно упрощает расчет напряженности.
Работа сил электростатического поля по перемещению заряда в поле не зависит от формы траектории. Это означает, что электростатическое поле является потенциальным полем, а, следовательно, взаимодействие электрических зарядов можно описывать с помощью потенциальной энергии. Понятие потенциальной энергии известно из механики, где показано, что работы по перемещению тела под действием силы в потенциальном поле равна изменению его потенциальной энергии с противоположным знаком. Найдем работу по перемещению заряда в электростатическом поле (Рис. 5).

Рис. 5
По
определению элементарная работа на
перемещении
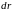 заряда
определяется
формулой:
заряда
определяется
формулой:
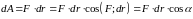 (14)
(14)
Тогда изменение потенциальной энергии заряда определяется формулой:
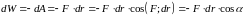 (15)
(15)
Так
как величина силы, действующей на заряд
в электростатическом поле, может быть
выражена через величину напряженности
по формуле
 ,
то изменение потенциальной энергии
можно определить формулой
,
то изменение потенциальной энергии
можно определить формулой
 (16)
(16)
Так как потенциальная энергия зависит от величины заряда, который перемещается в поле, то для характеристики электростатического поля вводится понятие потенциала. Потенциалом некоторой точки электростатического поля называется отношение потенциальной энергии к величине заряда, помещенного в изучаемую точку поля:
 (17)
(17)
Потенциал некоторой точки поля зависит от заряда, создающего поле, и от положения изучаемой точки поля. Потенциал не зависит от заряда, который помещается в некоторую точку поля. Единицей измерения потенциала является вольт (1В), который равен 1В=1Дж/Кл. Потенциал, а точнее разность потенциалов измеряется вольтметром.
Из формулы (17) получаем
 (18).
(18).
Приравнивая правые части формул (16) и (18), получаем:
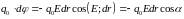 (19)
(19)
Из этой формулы следует связь между напряженностью и потенциалом:
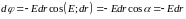 (20)
(20)
или
 (21)
(21)
Из
формул (20) и (21) следует, что вектор
напряженности в любой точке
электростатического поля направлен в
сторону убывания потенциала. Кроме того
величина
 представляет собой проекцию вектора
перемещения на линию напряженности
(Рис. 6).
представляет собой проекцию вектора
перемещения на линию напряженности
(Рис. 6).

Рис. 6
Тогда связь между напряженностью и потенциалом можно записать в виде:
 или
или
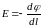 (22)
(22)
Кроме
того, величина
 (23) представляет собой проекцию вектора
напряженности электростатического
поля на вектор перемещения (Рис. 7).
(23) представляет собой проекцию вектора
напряженности электростатического
поля на вектор перемещения (Рис. 7).

Рис. 7
Тогда из формул (20) и (21) следует, что
 или
или
 (24)
(24)
В любом электростатическом поле можно выделить совокупность точек, потенциалы которых равны. Геометрическое место точек, потенциалы которых равны, называется эквипотенциальной поверхностью. Уравнение эквипотенциальной поверхности имеет вид:
 .
(25)
.
(25)
Как и линии напряженности, эквипотенциальные поверхности используются для графического представления полей.
Рассмотрим взаимное расположение линий напряженности и эквипотенциальных поверхностей. Работа по перемещению некоторого заряда по эквипотенциальной поверхности равна нулю, так как , то есть
 (26)
(26)
Кроме того работу по перемещению заряда можно найти по формуле
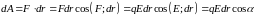 (27)
(27)
Приравниваем правые части формул (26) и (27) и получаем:
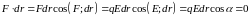 (28)
(28)
В
формуле (28)
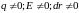 ,
тогда
,
тогда
 .
Это значит, что угол между линиями
напряженностей и эквипотенциальными
поверхностями электростатического
поля равен 900,
то есть линии напряженности и
эквипотенциальные поверхности взаимно
перпендикулярны (Рис. 8).
.
Это значит, что угол между линиями
напряженностей и эквипотенциальными
поверхностями электростатического
поля равен 900,
то есть линии напряженности и
эквипотенциальные поверхности взаимно
перпендикулярны (Рис. 8).

Рис. 8
Поэтому если на опыте можно построить эквипотенциальные поверхности, то перпендикулярные к ним линии будут линиями напряженности. Эквипотенциальные поверхности можно провести через точки поля. Эквипотенциальные поверхности принято проводить так, чтобы разность потенциалов между точками двух ближайших эквипотенциальных поверхностей была одинаковой.
