7.3 Неперервність функції в точці.

Визначення 2.

Функція y=f(x) буде неперервною в точці тоді і тільки тоді, коли виконуються такі умови:

1)функція визначена в точці і в деякому околі цієї точки;

2) існують кінцеві односторонні границі f( - 0) і f ( + 0)

3)виконуються рівняння f( - 0) = f ( + 0) = f( )

Якщо хоча б одна з цих умов не виконується , то функція називається розривною в точці , а сама точка називається точкою розриву функції.

Розрізняють такі види розривів. Якщо для функції f(x) існують скінчені границі , причому не всі числа f ( ), f( - 0), f ( + 0) рівні між собою, то розрив в точці називають розривом першого роду , точку -точкою розриву першого роду.

Зокрема, якщо , то розрив в точці називають усувним, а тому – точкою усувного розриву. У цьому випадку досить визначити функцію лише в одній точці , поклавши , щоб дістати функцію , неперервну в точці .

Величину називають стрибком функції.

Якщо хоча б одна з односторонніх границь не існує або дорівнює нескінченності , то розрив в точці – називається розривом другого роду, а сама точка - точкою розриву другого роду .

Приклади

1.Функція невизначена в точці х=0, але односторонні границі в цій точці існують, кінцеві і рівні між собою. f (0-0)=1 , f(0+0)=1

Досить покласти , щоб функція була неперервною.

Отже, функція

э неперервною в точці х=0.

2. Дослідити на неперервність функцію

Знайдемо

Стрибок в точці х=2 дорівнює

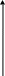
y 4 0 2 -1

3.Дослідити на неперервність функцію в точці х= -1.

Функція не визначена в точці х= -1, тому функція в цій точці розривна. Знайдемо односторонні границі.

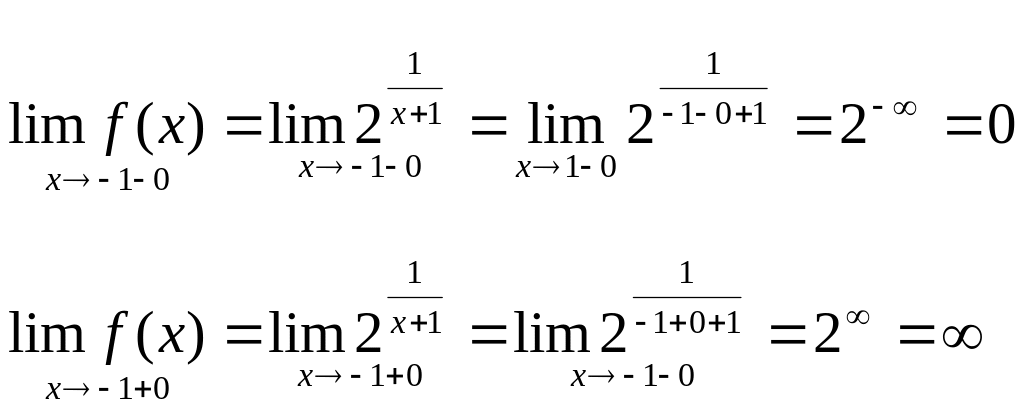
Розрив 2-го роду.

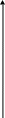
_y

₁

_{-1 0 x}

7.4 Неперервність функції на відрізку.

Якщо функція неперервна в кожній точці інтервали (а; b),то вона називається неперервною на цьому інтервалі.

Функція називається неперервною на відрізку [a;b] якщо вона неперервна на інтервалі (а; b) і, крім того, неперервна справа в точці а і зліва в точці b .

Сформулюємо властивості неперервних на відрізку функцій.

Т.1(перша теорема Больцано-Коші).

Якщо функція f(x) неперервна відрізку[a;b] і на його кінцях набирає значень різних знаків, то всередині відрізка [a;b] знайдеться хоча б одна точка х=с , в якій функція дорівнює нулю: f(c )=0 (a<c<b)

y f(a)>0 a с b x f(b)<0

T.2 (друга теорема Больцано-Коші).

Нехай функція y=f(x) неперервна на відрізку [a;b] і набуває на його кінця різних значень: f(a)=A f(b)=B, A≠B

Тоді для довільного числа знайдеться таке число µє [a;b], що f(c )=µ

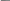
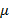
B A a c b

T.3 (Вейєрштрасса)

Якщо функція y=f(x) неперервна на відрізку [a;b], то серед її значень на цьому відрізку існує найменше і найбільше.

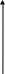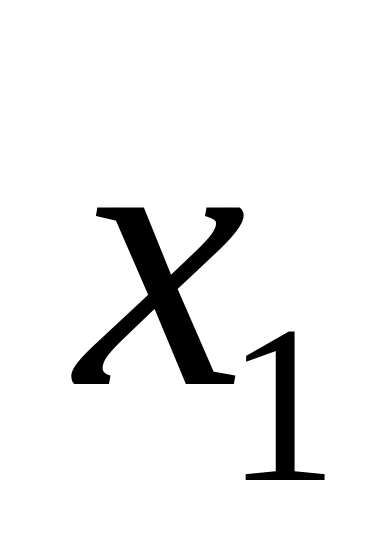
y M m a b x