3.4. Основні властивості нескінченно малих.

1. Сума скінченного числа нескінченно малих величин є величина нескінченно мала.

Нехай , де всі доданки справа – нескінченно малі. Тоді для мого числа ε>0 можна підібрати номер N, після якого одночасно будуть виконуватися нерівності . При цьому .

. А це і означає, що s – нескінченно мала.

2. Добуток обмеженої величини на нескінченно малу є величина нескінченно мала.

Нехай - нескінченно мала, а - обмежена величина. Завжди можна підібрати номер N, після якого одночасно будуть виконуватися нерівності | |<M; , де М – деяке, а ε – скіль завгодні малі додатні числа. При цьому .

Тобто , - нескінченно мала величина.

За обмежену величину може виступати стале число або деяка нескінченно мала величина. Таким чином:

1) добуток нескінченно малої на сталу є величина нескінченно стала мала.

2) добуток двох і більше нескінченно малих є величина нескінченно мала.

§4. Границя змінної

4.1 Границя послідовності

Число називають границею послідовності якщо для довільного числа існує номер N=N(ε), що при всіх n>N виконується нерівність

(1)

Якщо число є границею послідовності то пишуть

Розглянемо геометричний зміст границі послідовності. Нерівність (1) можна представить як

, або

Ці нерівності показують, що елемент x_n знаходиться в ε- околі точки .

Зауваження. Згідно наведеному вище, якщо існує , то змінну x_n завжди можна записати у формі , де α_n – деяка нескінченно мала величина.

Змінні по-різному наближуються до своєї границі. Значення змінної можуть зростати, спадати, коливатися:

x x

0 ½ 2/3 1 1 4/3 3/2 2

x

0 2/3 1 3/2 2

Якщо всі значення величини x_n співпадають з числом a, тобто x_n= a, то x_n – стала і в цьому випадку

,

Границя сталої є сама стала.

4.2.Властивості границі.

1. Змінна x_n не може мати дві різних границі. Дійсно, якби виявилось, що x_n→a і x_n→b для будь-якого ε>0, то починаючи з деякого номера N повинні виконуватися нерівності і , тобто значення x_n належать ε-околам точок a і b одночасно, а це неможливо.

Якщо змінна має границю, то ця границя одна.

2. Границя нескінченно малої величини є нуль і навпаки: якщо

, то x_n – нескінченно мала величина.

3. Якщо змінна x_n монотонна зростає і обмежена зверху, тобто для всякою номеру n x_n< x_n+1 <A = const, то існує скінченні границя

lim x_n=a ≤ A

4. У нерівності можна переходити до границі: якщо змінні x_n та y_n,тo

5. Якщо виконується нерівність (починаючи з деякого номера n) і змінні x_n та y_n мають одну й ту саму границю: x_n→a і y_n→a, то змінна z_n має ту й саму границю: z_n→a.

4.3. Границя суми, добутку і частки.

Якщо змінні x_n та y_n мають скінченні границі: , то їх сума, добуток і частка (при y_n≠0 і b≠0) також мають скінченні границі і справедливі формули

Доведемо це.

1. Дійсно, так як 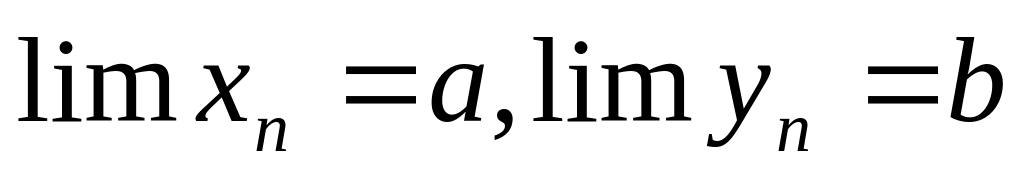, то 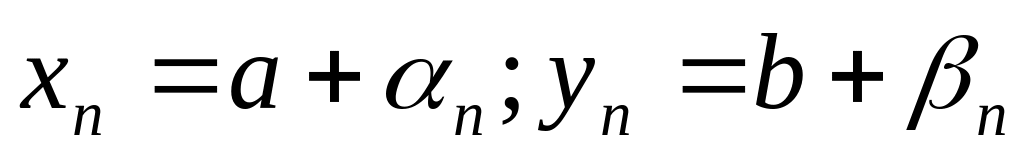, де α_n, β_n – деякі нескінченно малі. Маємо

₂₎

₃₎

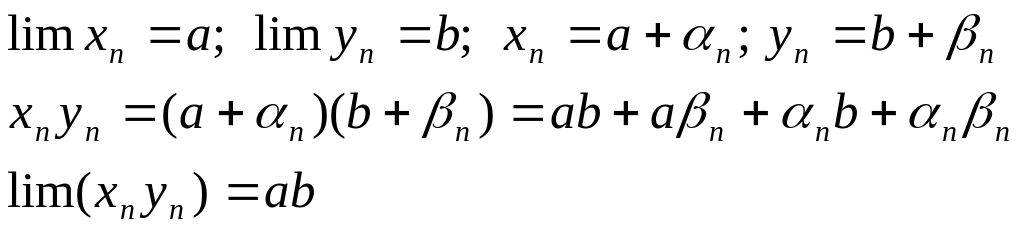
- обмежена величина. Тобто добуток обмеженої на нескінчену малу – н.м. і

Наслідок.