Пример выполнения
В
Mathcad комплексные вычисления
производятся с помощью символьного
процессора. Для выполнения операций
над комплексными числами мнимую единицу
j необходимо заранее
задать как
,
либо использовать стандартную мнимую
переменную i
коэффициентом 1 -
.
По окончании редактирования формулы
запись приобретает вид i.
Запишем частотную передаточную функцию апериодического звена первого порядка (параметры k и T следует либо задать перед описанием функции, либо их необходимо включить в список переменных функции):
.
При выходе из редактирования (щелчок мыши в свободном поле документа) формула приобретет вид
.
Выделим действительную и мнимую части амплитудно-фазовой частотной характеристики, используя функцию complex, которую можно выбрать в панели инструментов Математика в меню Символы:
,
.
Для
построения графиков частотных
характеристик (рис. 19) необходимо задать
диапазон изменения частоты, например,
,
коэффициент усиления
и постоянную времени
.
Рис. 19. Комплексная частотная характеристика
Амплитудная частотная характеристика рассчитывается следующим образом:
.
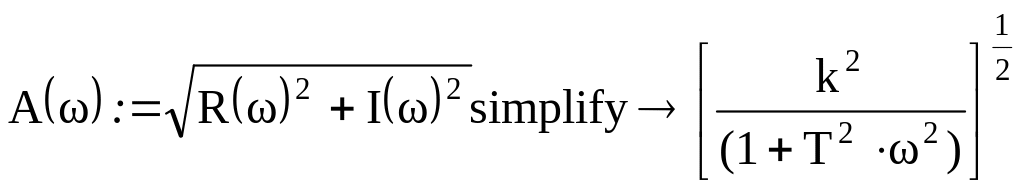Использование
функции simplify позволяет
упростить результат вычислений. Однако
последняя запись, полученная с помощью
Mathcad, может быть представлена
в более удобном виде:
.
График АЧХ показан ниже (рис. 20).
Рис. 20. Амплитудная частотная характеристика
Фазовую частотную характеристику (рис. 21) определим с помощью функции atan
.
Рис. 21. Фазовая частотная характеристика
Логарифмическая амплитудная характеристика рассчитывается как
.
Ее график показан на рис. 22.
При построении асимптотической ЛАХ, представляющей собой кусочно-линейную функцию, можно воспользоваться программным модулем (панель "Инструменты программирования").
Рис. 22. Логарифмическая амплитудная частотная характеристика
Для передаточной функции апериодического звена первого порядка асимптотическая ЛАХ (рис. 23) может быть построена по программе:
Рис. 23. Асимптотическая ЛАХ
Определение зависимости параметров гармонического сигнала на выходе линейного звена от частоты входного гармонического воздействия достаточно широко используется при экспериментальном определении частотных характеристик [10].
Моделирование прохождения гармонического сигнала через линейную систему осуществляется путем решения дифференциального уравнения
.
Преобразование
Лапласа от входного гармонического
сигнала
:
.
Выходной сигнал y(s) в преобразованиях Лапласа имеет вид
.
Выполняем обратные преобразования Лапласа и записываем выходной сигнал:
,
Строим графики сигналов на входе и выходе звена для различных частот (рис. 24 - 26):
Рис. 24. Сигналы на входе и выходе звена для =0.1
Рис. 25. Сигналы на входе и выходе звена для =0.5
Рис. 26. Сигналы на входе и выходе звена для =5
Как видно из рис. 24 – 26, при постоянной амплитуде входного гармонического сигнала, амплитуда сигнала на выходе апериодического звена с возрастанием частоты существенно уменьшилась, а смещение сигналов по фазе приблизилось к /2. Апериодическое звено работает как фильтр высоких частот.