5. Геометрический смысл производной. Возрастание и убывание функции. Максимум и минимум (экстремумы) функции.

Пусть некоторая функцияf(x) задана графически (например, см. рис.3), надо определить значение ее производной в некоторых точках А, В, С, D… графика этой функции (т.е при разных x). Геометрический смысл производной заданной функции состоит в том, что эта производная равна тангенсу угла между касательной, проведенной к графику функции в данной точке, и положительным на­правлением оси x.

Из рисунка видно, что если функция возрастает, производная положительна (=tg α, α - острый угол, tg α >0), если функция убывает, производная отрицательна (=tg β, β – тупой угол, tg β < 0). Если функция имеет максимальное (точка B) или минимальное значение (точка D), то касательная в этих точках экстремума параллельна оси x и производная f(x) при x = x₂ и x = x₄ равна нулю (tg 0 = 0).

Максимум и минимум функции можно различать между собой по знаку второй производной заданной функции в соответствующих точках. В точке максимума y'' < 0, а в точке минимума у'' > 0.

Исследование функции на максимум и минимум (на экстремум) рассмотрим на примере задачи 1 (стр.3).

Итак, надо ответить на вопрос: при какой дозе лекарства x реакция организма r будет максимальна?

Напомним, что r = x² (a – x) = ax² – x³, a > 0.

1. Найдем первую производную от заданной функции:

r' = 2ax – 3x²

2. Приравняем эту производную нулю и решим уравнение:

2ax – 3x² = 0, x(2a – 3x) = 0, решения уравнения: а) x = 0, оно лишено смысла, б) x = 2a/3.

2. Найдем вторую производную от r (первую производную от r'):

r'' = 2а – 6x,

Определим ее значение при x = 2a/3, r'' = - 2а < 0.

Следовательно, именно при x = 2a/3 реакция организма r будет максимальна.

В данной задаче величина а для каждого препарата определяется из экспериментальных данных.

6.Графики производных функций

В практической медицине часто приходится сопоставлять график изменения некоторой величины, например, со временем с графиком производной этой величины. В частности, в методе, называемом реопародонтография (см. лекцию №…) регистрируется зависимость объема кровенаполнения V исследуемого участка сосудистой системы от времени, т.е. V(t), и зависимость первой производной этой функции, которая определяет изменение скорости кровенаполнения. Примеры можно продолжить.

Д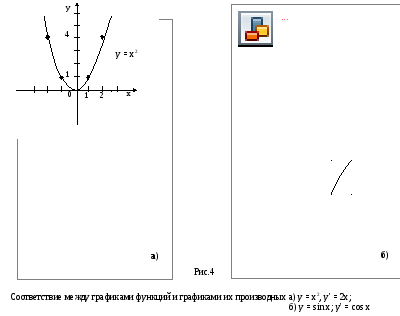ля нескольких простых функций приведем графики самих функций и их производных.

7.Дифференциал функции, его использование для оценки приращения функции.

Дифференциал заданной функции y = f(x) равен произведению значения производной этой функции в данной точке на дифференциал аргумента (d – символ дифференциала):

(9)

Можно показать, что дифференциал аргумента dx равен приращению аргумента Δx.

Дифференциал функции не равен приращению функции (dy ≠ Δy), но при малых приращениях Δх:

Δy ≈ dy (10)

Последний результат важен в прикладном отношении: зная дифференциал функции, можно оценить изменение этой функции и наоборот.

Приведем несколько примеров.

1. Найдем приближенное приращение функции y = 2x² + 7 при x = 2 и

Δx = 0,0001.

Решение: Δу≈ dy; dy = y' dx; dy = 4x dx или Δy ≈ 4x Δx

Таким образом, Δу ≈ 4 · 2 · 0,0001 = 0,0008.

2.Рассмотрим шарообразную клетку радиуса R (например, эритроцит в венозном русле), которая, не изменяя формы, увеличивается в объеме. Объем (V = f(R)). Оценим изменения объема клетки ΔV, если ее радиус увеличился от 2,5 · 10^-3 до 2,6· 10^-3 см.

Решение: ΔV≈ dV = V'dR = = 4π R²ΔR = 7,85 · 10^-9 см³.