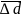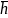- •Понятие о материи.
- •Погрешности
- •Для иллюстрации работы с функцией типа рассмотрим вычисление объема прямого кругового конуса V на основе прямых измерений его диаметра основания d и высоты h:
- •Определить работу тока за 8 секунд при силе тока 1,5а и напряжении 4в
- •Основная задача механики. Движение материальной точки.
- •Равномерное движение
- •Графическое представление движения.
- •Относительность движения
- •Неравномерное движение. Средняя скорость.
- •РавноПеременное прямолинейное движение. Мгновенная скорость. Ускорение.
- •Перемещение при прямолинейном равнопеременном движении.
- •2 . Определите перемещение тела, график проекции скорости которого, показан на рисунке
- •Движение материальной точки по окружности. Ц ентростремительное ускорение.
- •Период и частота обращения. Угловая скорость. Связь угловой и линейной скоростей.
- •Расчёт фрикционных, ремённых и зубчатых передач.
- •Как изменяются координаты тела со временем при равномерном движении по окружности.
- •Импульс. Закон сохранения импульса. II закон Ньютона. Взаимодействие двух или нескольких тел.
- •Импульс силы равен изменению импульса тела.
- •Р еактивное движение. Уравнение Мещерского. Формула Циолковского.
- •Энергия. Механическая работа и мощность. Энергия
- •Работа является мерой изменения энергии. Работа
- •Теорема о кинетической энергии
- •Векторные поля.
- •Ламинарное течение жидкости
- •Турбулентное течение жидкости. Вихревое поле.
- •Гравитационное поле
- •Строение солнечной системы.
- •Вес тела.
- •Вес тела движущегося с ускорением.
- •Э лектрическое поле
- •0,2 МкКл
- •Магнитное поле
- •Движение тела в однородных полях.
- •Движение тела в однородном гравитационном поле.
- •Движение тела, брошенного вертикально.
- •Движение тела, брошенного горизонтально.
- •Движение тела, брошенного под углом к горизонту.
- •2. Движение в однородном электрическом поле.
- •3. Движение частицы в магнитном поле.
- •С илы трения. Коэффициент трения. Трение в жидкостях и газах. Учёт и использование трения в быту и технике.
- •1. Сила трения
- •2. Сила сопротивления среды.
- •Сила гидростатического сопротивления.
- •2. Сила сопротивления вязкого трения.
- •Пример2. Падение тел в жидкости или газе.
- •Движение тел под действием нескольких сил.
- •2,2 М/с2 Лифт тормозится
- •Работа силы тяжести
- •Работа силы упругости
- •Коэффициент полезного действия
- •Потенциал. Работа и разность потенциалов. Эквипотенциальные поверхности.
- •1. Потенциальная энергия тяготения. Потенциал.
- •2. Работа и разность потенциалов
- •3. Потенциальная энергия электростатического взаимодействия. Потенциал электростатического поля.
- •4. Эквипотенциальные поверхности
- •Ёмкость. Теплоёмкость. Электроёмкость. Конденсаторы.
- •Соединение электрических конденсаторов.
- •Уравнения движения точки, равномерно движущейся по окружности. Колебательное движение.
- •Колебания
- •Характеристики колебательного движения:
- •Графики смещения, скорости и ускорения
- •Вынужденные гармонические колебания.
- •С ложение колебаний
- •Свободные гармонические колебания.
- •А втоколебания
- •Условия равновесия твёрдого тела. Виды равновесия. Принцип минимума потенциальной энергии. Момент силы. Условия равновесия тела, имеющего ось вращения.
- •Равновесие тела при наличии оси вращения.
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •Календарно-тематическое планирование
Для иллюстрации работы с функцией типа рассмотрим вычисление объема прямого кругового конуса V на основе прямых измерений его диаметра основания d и высоты h:

№ |
d (мм) |
(мм) |
∆d (мм) |
(мм) |
∆Аd (мм) |
h (мм) |
(мм) |
∆h (мм) |
(мм) |
∆Аh (мм) |
ɛd |
ɛh |
ɛV |
∆V (мм3) |
1 |
20 |
20 |
0 |
0,4 |
1,4 |
42 |
40 |
2 |
1,2 |
2,2 |
0,07 |
0,055 |
0,195 |
816 |
2 |
19 |
1 |
39 |
1 |
||||||||||
3 |
20 |
0 |
40 |
0 |
||||||||||
4 |
21 |
1 |
41 |
1 |
||||||||||
5 |
20 |
0 |
38 |
2 |
После проведения прямых измерений были вычислены средние статистические значения и диаметра и высоты соответственно, а также абсолютные погрешности ∆Аd = 1,35 мм и = 1,35 мм этих же величин.
∆d1= –d1 = 20 – 20 = 0(мм)
∆d2= –d2 = 20 – 19 = 1(мм)
∆d4=
–d4
=
 =
1(мм)
=
1(мм)
∆d5=
–d5
=
 =
0(мм)
=
0(мм)
 =0,4
(мм)
=0,4
(мм)
Погрешность прибора примем равной цене деления линейки δ=1мм.
 =
1,4 (мм)
=
1,4 (мм)
∆h1=
–h1
=
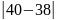 =
2(мм)
=
2(мм)
∆h2=
–h2
=
 =
1(мм)
=
1(мм)
∆h4=
–h4
=
 =
1(мм)
=
1(мм)
∆h5=
–h5
=
 =
2(мм)
=
2(мм)
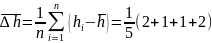 =
1,2 (мм)
=
1,2 (мм)
δ = 1(мм)
∆Аh = 1,2+1 = 2,2 (мм)


Численное
значение объема конуса
 вычисляется
по формуле
вычисляется
по формуле 4187
(мм3)
4187
(мм3)
Принимая
во внимание характер зависимости,
сначала выразим относительную погрешность
измерения объема конуса. В выражении
относительной погрешности пренебрежём
погрешностью π:

Вычисляем абсолютную погрешность ∆V=ɛV· = 0,195·4187 = 816 мм3, тогда окончательный результат можно записать в виде:
V
=
(4189 ± 816) мм3
.

К систематическим погрешностям можно отнести и погрешности отсчёта. Погрешность отсчета получается от недостаточно точного отсчитывания показаний средств измерений.
В большинстве случаев абсолютную погрешность отсчета принимают равной половине цены деления. Исключения составляют измерения стрелочными часами (стрелки передвигаются рывками).
Абсолютную погрешность отсчета принято обозначать ∆оА. Например, абсолютная погрешность измерения высоты ∆оh, при измерении линейкой с ценой деления 1мм, будет равна 0,5мм.
При отсутствии случайных погрешностей полная абсолютная погрешность равна сумме погрешности отсчёта и погрешности измерительного прибора.
Вычислим погрешность измерения коэффициента трения с помощью динамометра. Опыт заключается в том, что брусок равномерно тянут по горизонтальной поверхности и измеряют прикладываемую силу: она равна силе трения скольжения.
![]()
С помощью динамометра взвесим брусок с грузами: N = 1,8 Н измерим силу трения Fтр=0,6 Н получаем μ=0,33.
Инструментальная погрешность динамометра (находим по таблице) составляет Δ иР =0,05Н. Погрешность отсчета (половина цены деления)
Δ оР =0,05Н . Абсолютная погрешность измерения веса и силы трения 0,1 Н.
Относительная погрешность измерения
,![]()
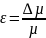 следовательно абсолютная погрешность
косвенного измерения ∆μ
составляет ∆μ
= ɛ·µ
= 0,22·0,33=0,074
следовательно абсолютная погрешность
косвенного измерения ∆μ
составляет ∆μ
= ɛ·µ
= 0,22·0,33=0,074
Вывод:
При
определении коэффициента трения
в
данной работе получен следующий результат
![]()