
- •Понятие о материи.
- •Погрешности
- •Для иллюстрации работы с функцией типа рассмотрим вычисление объема прямого кругового конуса V на основе прямых измерений его диаметра основания d и высоты h:
- •Определить работу тока за 8 секунд при силе тока 1,5а и напряжении 4в
- •Основная задача механики. Движение материальной точки.
- •Равномерное движение
- •Графическое представление движения.
- •Относительность движения
- •Неравномерное движение. Средняя скорость.
- •РавноПеременное прямолинейное движение. Мгновенная скорость. Ускорение.
- •Перемещение при прямолинейном равнопеременном движении.
- •2 . Определите перемещение тела, график проекции скорости которого, показан на рисунке
- •Движение материальной точки по окружности. Ц ентростремительное ускорение.
- •Период и частота обращения. Угловая скорость. Связь угловой и линейной скоростей.
- •Расчёт фрикционных, ремённых и зубчатых передач.
- •Как изменяются координаты тела со временем при равномерном движении по окружности.
- •Импульс. Закон сохранения импульса. II закон Ньютона. Взаимодействие двух или нескольких тел.
- •Импульс силы равен изменению импульса тела.
- •Р еактивное движение. Уравнение Мещерского. Формула Циолковского.
- •Энергия. Механическая работа и мощность. Энергия
- •Работа является мерой изменения энергии. Работа
- •Теорема о кинетической энергии
- •Векторные поля.
- •Ламинарное течение жидкости
- •Турбулентное течение жидкости. Вихревое поле.
- •Гравитационное поле
- •Строение солнечной системы.
- •Вес тела.
- •Вес тела движущегося с ускорением.
- •Э лектрическое поле
- •0,2 МкКл
- •Магнитное поле
- •Движение тела в однородных полях.
- •Движение тела в однородном гравитационном поле.
- •Движение тела, брошенного вертикально.
- •Движение тела, брошенного горизонтально.
- •Движение тела, брошенного под углом к горизонту.
- •2. Движение в однородном электрическом поле.
- •3. Движение частицы в магнитном поле.
- •С илы трения. Коэффициент трения. Трение в жидкостях и газах. Учёт и использование трения в быту и технике.
- •1. Сила трения
- •2. Сила сопротивления среды.
- •Сила гидростатического сопротивления.
- •2. Сила сопротивления вязкого трения.
- •Пример2. Падение тел в жидкости или газе.
- •Движение тел под действием нескольких сил.
- •2,2 М/с2 Лифт тормозится
- •Работа силы тяжести
- •Работа силы упругости
- •Коэффициент полезного действия
- •Потенциал. Работа и разность потенциалов. Эквипотенциальные поверхности.
- •1. Потенциальная энергия тяготения. Потенциал.
- •2. Работа и разность потенциалов
- •3. Потенциальная энергия электростатического взаимодействия. Потенциал электростатического поля.
- •4. Эквипотенциальные поверхности
- •Ёмкость. Теплоёмкость. Электроёмкость. Конденсаторы.
- •Соединение электрических конденсаторов.
- •Уравнения движения точки, равномерно движущейся по окружности. Колебательное движение.
- •Колебания
- •Характеристики колебательного движения:
- •Графики смещения, скорости и ускорения
- •Вынужденные гармонические колебания.
- •С ложение колебаний
- •Свободные гармонические колебания.
- •А втоколебания
- •Условия равновесия твёрдого тела. Виды равновесия. Принцип минимума потенциальной энергии. Момент силы. Условия равновесия тела, имеющего ось вращения.
- •Равновесие тела при наличии оси вращения.
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •I вариант
- •II вариант
- •Календарно-тематическое планирование
Теорема о кинетической энергии

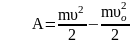
Пусть
тело движется по горизонтальной
поверхности под действием силы тяги.
Сила трения равна нулю, тогда работа
силы тяги A=Fтяги
S,
(cosφ=1,
т.к.φ=0). Fтяги=ma,
 ,
отсюда
,
отсюда
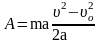 ,
или
,
или
 назовём
кинетической энергией тела.
назовём
кинетической энергией тела.
Работа силы (или равнодействующей сил) равна изменению кинетической энергии тела. Это утверждение называется теоремой о кинетической энергии.
Работа является мерой изменения энергии.
А = Е2 – Е1
Пример: Какую работу нужно совершить для увеличения скорости поезда υ1=72км/час, до скорости υ2=108км/час? Масса поезда 1000т. Какова должна быть сила тяги локомотива, если это увеличение должно произойти на участке длиной 2000м?
Дано: υо=72км/час - 20м/с υ=108км/час-30 м/с m=1000т - 103кг S=2000м А=? Fтяги=? |
|
Для
определения работы используем формулу
Ответ: При увеличении скорости поезда, совершается работа 2,5х108Дж и развивается тяговое усилие 125кН.
|
Работу
можно производить медленно или быстро.
Быстрота производимой работы называется
мощностью.
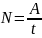 и измеряется в Ваттах (Вт). При равномерном
движении имеем:
и измеряется в Ваттах (Вт). При равномерном
движении имеем:
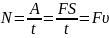 .
При постоянной мощности можно увеличить
силу тяги за счёт уменьшения скорости
(пониженная передача) на подъёме Или
наоборот увеличить скорость на ровном
участке шоссе, но при этом уменьшится
сила тяги.
.
При постоянной мощности можно увеличить
силу тяги за счёт уменьшения скорости
(пониженная передача) на подъёме Или
наоборот увеличить скорость на ровном
участке шоссе, но при этом уменьшится
сила тяги.
Вопросы :
Что такое энергия?
Какие виды энергии вы знаете?
Что является мерой изменения энергии?
Что такое работа?
Чему равно скалярное произведение двух векторов?
Как графически определить работу?
Что называется мощностью?
По какой формуле вычисляется мощность?
Что называется кинетической энергией тела?
О чём гласит теорема о кинетической энергии?
ДОМАШНЕЕ ЗАДАНИЕ 16
Какую работу нужно совершить для увеличения скорости поезда υ1=54км/час, до скорости υ2=72км/час? Масса поезда 1500т. Какова должна быть сила тяги локомотива, если это увеличение должно произойти на участке длиной 2000м?
Сплавщик передвигает багром плот, прилагая к багру силу 200 Н. Какую работу совершит сплавщик, переместив плот на 10 м, если угол между направлением силы и направлением перемещения 45° ?
1,4 кДж
При равномерном спуске груза по наклонному настилу тормозящая сила 1 кН направлена под углом 150° к направлению движения груза. Определите работу тормозящей силы, если длина настила 5 м.
-4,3 кДж
Сила тяги сверхзвукового самолета при скорости полета 2340 км/ч равна 220 кН. Найти мощность двигателей самолета в этом режиме полета.
143 МВт
Мощность электровоза равна 4000 кВт. Найдите силу тяги электровоза при скорости движения 72 км/ч.
2 00
кН
00
кН
Векторные поля.
Существует четыре фундаментальных взаимодействия: гравитационное, электромагнитное, сильное и слабое. Вся совокупность элементарных частиц с их взаимодействиями проявляет себя в форме вещества и поля. Поле в отличие от вещества обладает особыми свойствами. Оно распределено в пространстве и передаёт взаимодействие. Электромагнитное поле может существовать самостоятельно, например свет, радиоволны. Они имеют конечную скорость распространения. Гравитационное поле реально ощутимо вокруг массивных тел. Источником электромагнитного поля являются движущиеся заряженные частицы. Взаимодействие зарядов происходит по схеме частица – поле – частица. Схема гравитационного взаимодействия, вероятно, такая же. В некоторых условиях поле может оторваться от источника и свободно распространяться в пространстве. Такое поле носит волновой характер.
С остояние
материальной точки задавалось её
положением в пространстве и её скоростью.
Такой способ описания непригоден для
полей. Основное свойство полей - передача
взаимодействия (силы). Поле определено,
если для каждой точки пространства
известны значения вектора
напряжённости.
Напряжённость
поля – вектор численно равный силе
действующей на тело, обладающего единицей
величины, характеризующей данное
взаимодействие.
Линии, в каждой точке которой вектор
напряжённости является касательным,
называются силовыми линиями или линиями
вектора напряжённости.
остояние
материальной точки задавалось её
положением в пространстве и её скоростью.
Такой способ описания непригоден для
полей. Основное свойство полей - передача
взаимодействия (силы). Поле определено,
если для каждой точки пространства
известны значения вектора
напряжённости.
Напряжённость
поля – вектор численно равный силе
действующей на тело, обладающего единицей
величины, характеризующей данное
взаимодействие.
Линии, в каждой точке которой вектор
напряжённости является касательным,
называются силовыми линиями или линиями
вектора напряжённости.
Для описания векторных полей очень удобным оказываются понятия потока и циркуляции поля.
Э лементарный
поток
векторного поля
лементарный
поток
векторного поля
 через
поверхность ΔS
равен
через
поверхность ΔS
равен
ΔФ=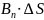 , где ΔФ – элементарный поток вектора
,
Вn
– проекция вектора
на нормаль к поверхности, ΔS
– элементарная поверхность. Для того,
что бы вычислить полный поток вектора
через поверхность необходимо сложить
элементарные потоки.
, где ΔФ – элементарный поток вектора
,
Вn
– проекция вектора
на нормаль к поверхности, ΔS
– элементарная поверхность. Для того,
что бы вычислить полный поток вектора
через поверхность необходимо сложить
элементарные потоки.
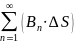 =
(Bn)1∙ΔS1+(Bn)2∙ΔS2+(Bn)3∙ΔS3+(Bn)4∙ΔS4+(Bn)5∙ΔS5+
….+(Bn)n∙ΔSn
=
(Bn)1∙ΔS1+(Bn)2∙ΔS2+(Bn)3∙ΔS3+(Bn)4∙ΔS4+(Bn)5∙ΔS5+
….+(Bn)n∙ΔSn
В
короткой записи это выглядит так: Ф
=


Элементарная циркуляция векторного поля вдоль замкнутого контура равна
ΔГ=Вτ·Δℓ, где ΔГ – элементарная циркуляция вектора , Вτ – проекция вектора на касательную к точке контура, Δℓ - длина элементарного участка контура. Полную циркуляцию по замкнутому контуру можно вычислить, если сложить элементарные циркуляции.
Г = Вτ1∙ℓ+
Вτ2∙ℓ+
Вτ3∙ℓ+
Вτ3∙ℓ+…
Вτn∙ℓ
или
= Вτ1∙ℓ+
Вτ2∙ℓ+
Вτ3∙ℓ+
Вτ3∙ℓ+…
Вτn∙ℓ
или
Г=
ВОПРОСЫ:
Какие фундаментальные взаимодействия вы знаете?
Какие функции выполняют поля?
Что называется напряжённостью поля?
Что называется линиями напряжённости поля?
Что называется элементарным потоком векторного поля через поверхность ΔS?
Что называется элементарной циркуляцией вектора напряжённости вдоль замкнутого контура?



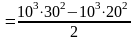 =2,5х108Дж
Если A=FS,
то F=A/S
F=2,5х108/2000=1,25х105Н
=2,5х108Дж
Если A=FS,
то F=A/S
F=2,5х108/2000=1,25х105Н