1 Алгоритм des
Американський стандарт криптографічного захисту даних (Data Encryption Standard), прийнятий в 1978 році є типовим представником сімейства блочних шифрів. Цей шифр допускає ефективну апаратну та програмну реалізації, причому можливо досягнення швидкостей до декількох мегабайтів за секунду.
Алгоритм DES виконує шифрування 64-бітних блоків даних за допомогою 56 бітного ключа. Дешифрування в DES є оберненою операцією шифруванню і виконується шляхом повторення операцій шифрування в зворотній послідовності.
Процес шифрування полягає в початковій перестановці 64 бітів вхідного блоку, шістнадцяти циклах шифрування та зворотній перестановці бітів (рис. 1)
Необхідно звернути увагу на те, що всі таблиці алгоритму DES є стандартними і повинні включатися в реалізацію алгоритму в незмінному вигляді. Усі перестановки і коди в таблицях підібрані так, щоб зробити максимально важким процес зламування шляхом підбору ключа.
Рисунок 1 – Загальна схема процесу шифрування в алгоритмі DES
Розглянемо алгоритм докладніше.
Припустимо, з файлу зчитано 64-бітний
блок
,
який перетворюється за допомогою
початкової перестановки IP
(рис. 2)
в 64-бітний блок
.
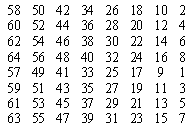
Рисунок 2
– Матриця початкової перестановки
Після IP-перестановки
16 разів повторюється процедура шифрування
блока
за допомогою функції
.
Позначимо
– результат i-ї
ітерації;
– перші (ліві) 32 біти блоку
,
;
– останні (праві) 32 біти блоку
,
.
Таким чином,
.
Тоді результатом i-ї операції буде:
,
,
де
– операція додавання за
модулем 2;
– i-те
перетворення ключа шифрування
.
Функція
виконує операції над значенням
(результатом минулої операції) та
поточним значенням 48-бітного ключа
(з відокремленням зайвих бітів). До речі,
після 16-ї ітерації ліва і права половини
блока не міняються місцями (рис. 3).
По закінченні шифрування виконується
відновлення позицій бітів за допомогою
матриці перестановок
(рис. 4).
Розглянемо докладніше функцію
.
Крок 1 На
кожній ітерації масив
розширюється до 48 бітів за допомогою
таблиці розподілення бітів
.
Блок
розбивається на вісім блоків по 4 біти
(рис. 5).
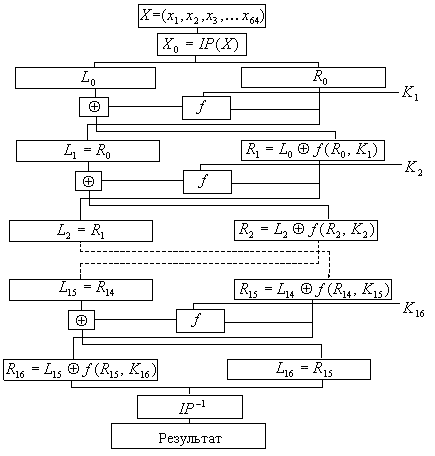
Рисунок 3 – Загальна схема алгоритму шифрування DES
Шляхом копіювання крайніх
елементів вісім 4-бітних блоки
перетворюються у вісім 6-бітних блоків
(рис. 6). Отриманий блок
має
48 бітів.
-
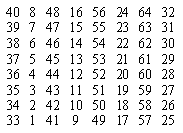
Рисунок 4 – Матриця зворотної перестановки
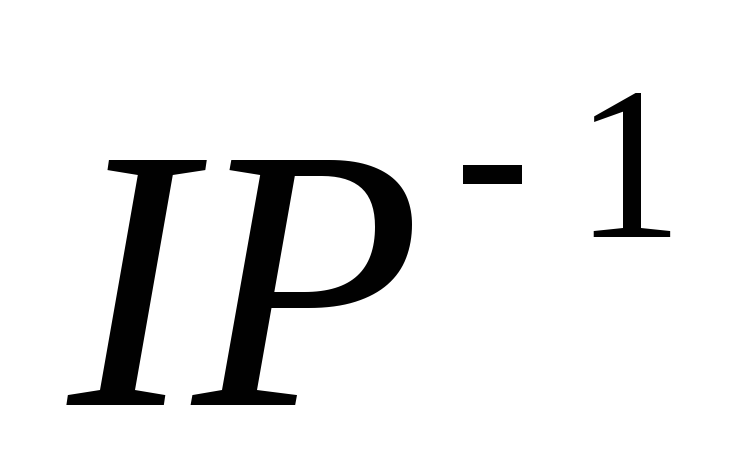
Рисунок 5 – Розбиття
на вісім блоків
Крок 2 Блок
порозрядно сумують за модулем 2 з
поточним значенням ключа
, а потім розбивають на вісім 6-бітних
блоки
,
тобто
.
Крок 3 Кожен
блок (
)
подається на вхід підстановки S-бокс
(рис 7). Індекс
вказує, який з масивів S-боксу
використовувати. Застосувавши операцію
вибору до кожного із блоків
,
одержимо 32-бітний потік.
Рисунок 6
– Таблиця розподілення бітів
Відзначимо, що вибір елемента
в масиві
здійснюється досить оригінальним
способом. Нехай на вхід подається
6-бітний блок
,
дві крайні позиції
інтерпретуються як двійкове подання
цілих чисел з набору {0, 1, 2, 3}.
|
|
Номер стовпця |
|
||||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|||
|
Номер рядка |
0 |
14 |
4 |
13 |
1 |
2 |
15 |
11 |
8 |
3 |
10 |
6 |
12 |
5 |
9 |
0 |
7 |
S1 |
|
1 |
0 |
15 |
7 |
4 |
14 |
2 |
13 |
1 |
10 |
6 |
12 |
11 |
9 |
5 |
3 |
8 |
||
|
2 |
4 |
1 |
14 |
89 |
13 |
6 |
2 |
11 |
15 |
12 |
9 |
7 |
3 |
10 |
5 |
0 |
||
|
3 |
15 |
12 |
8 |
2 |
4 |
9 |
1 |
7 |
5 |
11 |
3 |
14 |
10 |
0 |
6 |
13 |
||
|
0 |
15 |
1 |
8 |
14 |
6 |
11 |
3 |
4 |
9 |
7 |
2 |
13 |
12 |
0 |
5 |
10 |
S2 |
|
|
1 |
3 |
13 |
4 |
7 |
15 |
2 |
8 |
14 |
12 |
0 |
1 |
10 |
6 |
9 |
11 |
5 |
||
|
2 |
0 |
14 |
7 |
11 |
10 |
4 |
13 |
1 |
5 |
8 |
12 |
6 |
9 |
3 |
2 |
15 |
||
|
3 |
13 |
8 |
10 |
1 |
3 |
15 |
4 |
2 |
11 |
6 |
7 |
12 |
0 |
5 |
14 |
9 |
||
|
0 |
10 |
0 |
9 |
14 |
6 |
3 |
15 |
5 |
1 |
13 |
12 |
7 |
11 |
4 |
2 |
8 |
S3 |
|
|
1 |
13 |
7 |
0 |
9 |
3 |
4 |
6 |
10 |
2 |
8 |
5 |
14 |
12 |
11 |
15 |
1 |
||
|
2 |
13 |
6 |
4 |
9 |
8 |
15 |
3 |
0 |
11 |
1 |
2 |
12 |
5 |
10 |
14 |
7 |
||
|
3 |
1 |
10 |
13 |
0 |
6 |
9 |
8 |
7 |
4 |
15 |
14 |
3 |
11 |
5 |
2 |
12 |
||
|
0 |
7 |
13 |
14 |
3 |
0 |
6 |
9 |
10 |
1 |
2 |
8 |
5 |
11 |
12 |
4 |
15 |
S4 |
|
|
1 |
13 |
8 |
11 |
5 |
6 |
15 |
0 |
3 |
4 |
7 |
2 |
12 |
1 |
10 |
14 |
9 |
||
|
2 |
10 |
6 |
9 |
0 |
12 |
11 |
7 |
13 |
15 |
1 |
3 |
14 |
5 |
2 |
8 |
4 |
||
|
3 |
3 |
15 |
0 |
6 |
10 |
1 |
13 |
8 |
9 |
4 |
5 |
11 |
12 |
7 |
2 |
14 |
||
|
0 |
2 |
12 |
4 |
1 |
7 |
10 |
11 |
6 |
8 |
5 |
3 |
15 |
13 |
0 |
14 |
9 |
S5 |
|
|
1 |
14 |
11 |
2 |
12 |
4 |
7 |
13 |
1 |
5 |
0 |
15 |
10 |
3 |
9 |
8 |
6 |
||
|
2 |
4 |
2 |
1 |
11 |
10 |
13 |
7 |
8 |
15 |
9 |
12 |
5 |
6 |
3 |
0 |
14 |
||
|
3 |
11 |
8 |
12 |
7 |
1 |
14 |
2 |
13 |
6 |
15 |
0 |
9 |
10 |
4 |
5 |
3 |
||
|
0 |
12 |
1 |
10 |
15 |
9 |
2 |
6 |
8 |
0 |
13 |
3 |
4 |
14 |
7 |
5 |
11 |
S6 |
|
|
1 |
10 |
15 |
4 |
2 |
7 |
12 |
9 |
5 |
6 |
1 |
13 |
14 |
0 |
11 |
3 |
8 |
||
|
2 |
9 |
14 |
15 |
5 |
2 |
8 |
12 |
3 |
7 |
0 |
4 |
10 |
1 |
13 |
11 |
6 |
||
|
3 |
4 |
3 |
2 |
12 |
9 |
5 |
15 |
10 |
11 |
14 |
1 |
7 |
6 |
0 |
8 |
13 |
||
|
0 |
4 |
11 |
2 |
14 |
15 |
0 |
8 |
13 |
3 |
12 |
9 |
7 |
5 |
10 |
6 |
1 |
S7 |
|
|
1 |
13 |
0 |
11 |
7 |
4 |
9 |
1 |
10 |
14 |
3 |
5 |
12 |
2 |
15 |
8 |
6 |
||
|
2 |
1 |
4 |
11 |
13 |
12 |
3 |
7 |
14 |
10 |
15 |
6 |
8 |
0 |
5 |
9 |
2 |
||
|
3 |
6 |
11 |
13 |
8 |
1 |
4 |
10 |
7 |
9 |
5 |
0 |
15 |
14 |
2 |
3 |
12 |
||
|
0 |
13 |
2 |
8 |
4 |
6 |
15 |
11 |
1 |
10 |
9 |
3 |
14 |
5 |
0 |
12 |
7 |
S8 |
|
|
1 |
1 |
15 |
13 |
8 |
10 |
3 |
7 |
4 |
12 |
5 |
6 |
11 |
0 |
14 |
9 |
2 |
||
|
2 |
7 |
11 |
4 |
1 |
9 |
12 |
14 |
2 |
0 |
6 |
10 |
13 |
15 |
3 |
5 |
8 |
||
|
3 |
2 |
1 |
14 |
7 |
4 |
10 |
8 |
13 |
15 |
12 |
9 |
0 |
3 |
5 |
6 |
11 |
||
Рисунок 7 – S-бокс
Ці числа визначають номер
рядка (від 0 до 3) масиву
.
Чотири біти, що залишилися,
інтерпретуються як двійкове подання
цілих чисел з набору {0, 1, 2, … , 15} і
використовуються для визначення стовпця
(від 0 до 15) у масиві
.
Таким чином, вхідний блок,
наприклад,
,
відповідає десятковому числу 9, розміщеному
в другому рядку та в третьому стовпці
масиву
, Число 9 у двійковому поданні являє
собою 4-бітний блок (1001).
У результаті застосувавши
до кожного з блоків
( 
)
операцію вибору в S-боксі,
одержимо 32-бітний блок
.
Крок 4
Отриманий блок
перетворюється за допомогою матриці
перестановки
(рис. 8).
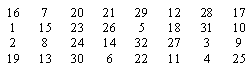
Рисунок 8
– Матриця перестановки
Таким чином,
.