
О.О.П / ооп / 4_кол / К курсовой / Методи побудови алгоритмів та їх аналіз. Караванова Т.П. / 62_201
.PDFкоротший шлях від заданої вершини до шуканої. Для того щоб остаточно у цьому пересвідчитися, далі ми перейдемо до іншого методу - пошуку в глибину.
Спробуємо провести оцінку алгоритму пошуку в ширину. Під час формування черги з вершин заданого графа, що скла дається з п вершин і т ребер, кожна вершина переглядається лише один раз. Це відповідає оцінці О(п). Але при цьому пере глядаються всі ребра, яким належить поточна вершина. Отже, оцінка перегляду ребер становить О(т). Оскільки перегляд ребер іде паралельно з переглядом вершин, що їм належать, то остаточна оцінка алгоритму визначається як 0(п + пі). Отже, можна зробити висновок, що час роботи алгоритму прямо пропорційний розміру заданого графа.
Завдання
1.Розробити і реалізувати у вигляді програми алгоритм пошу ку в ширину.
2.Виконати завдання 1 для графа з кількістю вершин N = 5, в якому досліджувані вершини є досяжними. Результат вико нання програми вивести у файл.
3.Виконати завдання 1 для графа з кількістю вершин N = 5, в якому досліджувані вершини є недосяжними. Результат ви конання програми вивести у файл.
4.Виконати завдання 2-3 для N = 100, вивівши результат ви конання програми у файл.
Пошук у глибину
Якщо під час пошуку в ширину ми захоплювали усі нові вер шини, що нам було видно з поточної вершини, у яку переміщува лися на кожному наступному кроці, то під час пошуку в глибину дещо змінимо нашу стратегію. А полягатиме вона ось у чому.
На кожному кроці алгоритму, знаходячись у наступній по точній вершині, будемо бачити лише одну нову, досі не «види му», вершину і переходити до неї.
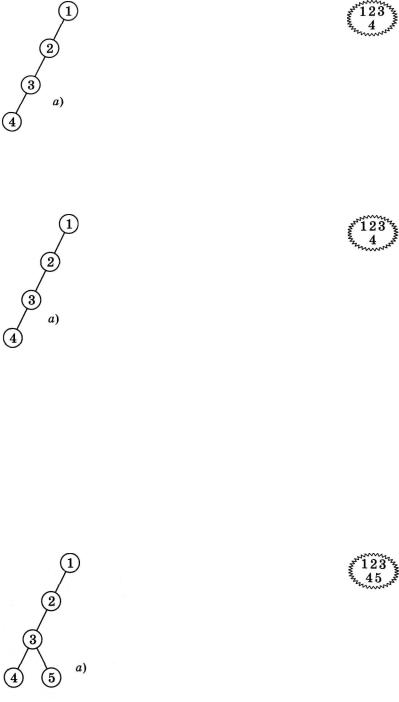
Розглянемо той самий граф, що й у попередньому випадку (мал. 21, а), і його таблицю суміжності (мал. 21, б). Будемо знову шукати шлях від вершини 1 до вершини 7. Під час по шуку будемо так само, як і в попередньому алгоритмі, будува ти дерево пошуку, послідовність переглянутих і нових «види мих» вершин та множину «відвіданих» вершин. На малюнку 29, а, б, в зображено перший крок нашого алгоритму, який повністю збігається з першим кроком алгоритму пошуку в ширину.
62

® 4
a) |
6) |
в) |
Мал. 29
Наступний крок буде таким: згідно з таблицею суміжності першою новою вершиною, яку ми бачимо з вершини 1, є вер шина 2. Перейдемо до неї, додавши її у дерево пошуку, в по слідовність «відвіданих» вершин і у множину (мал. ЗО, а, б, в).
-0
1 2
б) |
в) |
4
1 2 3
д) |
є) |
г)
Мал. ЗО
Перейшовши тепер у вершину 2, згідно з таблицею суміж ності першою новою «видимою» вершиною є вершина З, оскільки вершину 1 ми вже відвідали. Додамо цю нову верши ну до нашого дерева пошуку, в послідовність та множину (мал. ЗО, г, д, є) і перейдемо у послідовності до неї.
Якщо на наступному кроці алгоритму ми подивимося з вер шини 3, то зможемо побачити вершини у такій послідовності (третій рядок таблиці суміжності): 1, 2, 4, 5. Серед них першою новою вершиною є вершина 4. Додамо її до переглянутих і пе рейдемо до неї (мал. 31, а, б, в).
Що нового ми побачимо з вершини 4? Згідно з малюн ком 21, а, б, ми побачимо вершини 1 і 3. Але жодна з них не є новою. Невже ми потрапили в тупик? Мабуть, ні, оскільки з попереднього методу пошуку в ширину ми дійшли до шуканої
63
4
1 2 3 4
б) |
в) |
Мал. 31
вершини. Можливо, ми пішли не тим шляхом і треба спробу вати повернутися назад? Попередньою вершиною була верши на 3, і ми повернемося саме до неї (мал. 32, б).
£
1 2 3 4
—і — і — і —
б) |
в) |
Мал. 32
Подивимося на заданий граф: чи є з вершини 3 інший шлях, відмінний від верпіини 4? Так, це шлях через вершину 5. І ця вершина є наступною новою вершиною, яку ми можемо поба чити з вершини 3. Перейдемо до неї, записавши її у дерево по шуку, замінивши у послідовності нею вершину 4 та дописавши її у множину (мал. 33, о, б, в).
Застосуємо нашу стратегію до останньої «переглянутої» вер шини 5. З неї ми бачимо вершини 2, 3, 7. Але серед них верши на 7 є новою і одночасно шуканою. Саме тому дописуємо її в усі три інформаційні схеми (мал. 34, а, б, в) та вважатимемо по шук завершеним.
|
|
|
4 |
1 |
2 |
3 |
5 |
|
|
б) |
в) |
Мал. 33
64

Мал. 34
Ми знайшли відповідь на запитання за допомогою алгорит му пошуку в глибину: у заданому графі вершина 7 є досяжною з вершини 1 і шлях до неї міститься у послідовності, зобра женій на малюнку 34, б.
Дивлячись на малюнок 21, а, де зображено досліджуваний граф, можна переконатися, що це справді шлях від вершини 1 до вершини 7. Однак отримана відповідь не збігається з відпо віддю, одержаною за допомогою алгоритму пошуку в ширину. У чому ж справа? Ми повернемося до цього питання трохи зго дом, порівнюючи ці два методи, а зараз визначимося з питан ням реалізації цього алгоритму.
Як видно з покрокового виконання описаного алгоритму, ми весь час працюємо з таблицею суміжності, беручи звідти інфор мацію про одну нову «видиму» вершину із поточної вершини графа. Ця нова вершина записується у послідовність, яка оброб ляється за алгоритмом роботи зі стеком: ми дописуємо нову інформацію в кінець цієї послідовності і, у разі потрапляння у тупик, повертаємося до її передостаннього елемента, не роз глядаючи надалі останній записаний елемент послідовності. І на останок: для запобігання повернення у тупикові вершини інфор мацію про всі відвідані вершини зберігатимемо у множині.
Ми розглянули алгоритм пошуку в глибину на прикладі гра фа, де шукана вершина є досяжною із заданої, і отримали пози тивну відповідь стосовно існування шляху між цими двома вер шинами. А в іншій ситуації як дізнатися, що шлях відсутній? Згадаємо, як ми діяли у випадку, коли потрапляли у тупик. Ми поверталися до попередньої «переглянутої» вершини і намага лися знайти іншу нову, ще не «побачену», вершину. Логічно, що коли такої немає, то ми повернемося до попередньої віднос но неї і будемо шукати вихід із цієї вершини і т. д. У разі відсут ності шляху між двома заданими вершинами ми завершимо перегляд усіх записаних у стек вершин, повертаючись кожного разу до попередньої, спорожнивши тим самим стек. Отже,
З Інформатика, 9-Ю кл. |
65 |
ознакою відсутності шляху в графі між двома заданими верши нами є те, що на деякому кроці алгоритму стек стане порожнім.
Сформулюємо описаний алгоритм пошуку в глибину у сло весній формі.
1.Вказати номер вершини k, з якої починається пошук за даної шуканої вершини І. •
2.Почати перегляд вершин заданого графа з вершини k, за писавши її у стек: і := k.
3.Якщо існує нова вершина з найменшим порядковим но мером, яку можна побачити з вершини і, то зафіксувати її, за писавши у стек і збільшивши при цьому індекс вершини сте ку і на 1: і := і + 1. У протилежному випадку перейти до п. 5.
4.Якщо нова «побачена» вершина, записана у стек, є шука ною, то перейти до п. 7.
5.Якщо з поточної вершини графа, яка записана у вершині стеку, не видно жодної нової вершини, то відкинути цю верши ну, перейшовши до попередньої у стеку, зменшивши для цього значення індексу вершини стеку на 1: і := і - 1. Якщо після цьо го стек став порожнім, тобто і = 0, то перейти до п. 9.
6.Перейти до перегляду наступної «побаченої» вершини і (п. 3).
7.Вивести інформацію про те, що шукану вершину / досяг нуто і шлях до неї від вершини k існує.
8.Перейти до п. 10.
9.Вивести інформацію про те, що шукана вершина І недо сяжна від вершини k і шлях до неї відсутній.
10.Завершити алгоритм.
Наведемо фрагменти алгоритму пошуку в глибину у вигляді Pascal-програми:
top '.- 1; а[1] := к; {Ініціалізація роботи алгоритму.}
flag := false; s := [к];
while (top > 0) and not flag do {Поки стек не порожній і не знайдено шукану}
begin |
{верш |
І := 1; |
{починаємо пошук нової «видимої» вершини.} |
while (І <= n) and not flag do {Пошук нової «видимої» вершини з /с-ї вершини.}
begin |
|
|
if ( d [ a [ t o p ] , І] = 1) and not (і in s) |
{Якщо існує нова «видима» вершина,} |
|
then |
|
|
begin |
|
|
inc(top); a[top] |
:= і; |
{то записуємо її у стек і} |
s : = S + [ i ] ; |
|
{заносимо у множину.} |
if І = І then flag := true; {Якщо нова вершина є шуканою, то фіксуємо це.} |
||
end |
|
|
else ІПС(І) |
{Інакше переходимо до нової «побаченої» вершини.} |
|
end; |
|
|
if not false then dec(top) |
{Якщо відсутні нові «видимі» вершини,} |
|
end; |
|
{т° повертаємося до попередньої.} |
66
Для виведення визначеного шляху між двома заданими вер шинами графа можна використати такий фрагмент:
.
if flag t h e n |
{Якщо шлях знайдено, то} |
b e g i n |
|
writeln(f _ out, 'YES'); |
{виводимо інформацію про це і} |
w h i l e top < > O d o |
|
b e g i n |
{виводимо послідовність} |
І write(f_out, a[top],''); dec(top) |
{елементів стеку.} |
end |
|
end |
|
e l s e write(f_OUt, 'NO'); {Виведення інформації про відсутність шляху.}
Тепер ми вже готові до порівняння двох пошукових методів на графах у ширину та в глибину.
Спочатку відповімо на таке слушне запитання: чому у наведе ному прикладі графа ми отримали різні відповіді, хоча кожна з них є правильною? А це відбулося тому, що для методів обрані різні стратегії: під час пошуку в ширину ми послідовно перегля даємо усі видимі вершини і таким чином якнайшвидше досягне мо шуканої вершини, а під час пошуку в глибину на кожному кроці ми переглядаємо лише одну нову вершину і тому можемо піти у хибному напрямі. Отже, можна зробити висновок, що ал горитм пошуку в ширину завжди визначає найкоротший шлях між двома заданими вершинами графа.
Який з методів кращий? Однозначно на це запитання відпо вісти неможливо. Стосовно реалізації методів, можливо, по шук у глибину простіший, оскільки одразу в стеку отримуємо шуканий шлях, та й при організації роботи зі стеком виникає менше помилок. Однак цей метод не завжди визначає найко ротший шлях між заданими вершинами. І відповідь про відсутність шляху в разі використання пошуку в ширину може бути отримана швидше, ніж під час пошуку в глибину. Однак реалізація алгоритму пошуку в ширину вимагає організації та кої структури даних, як черга, і більш складної стратегії визна чення шляху між двома заданими вершинами.
Логічним є запитання про те, де можна застосовувати ці ал горитми. По-перше, це пряме їх використання щодо визначен ня шляху між двома заданими вершинами графа. По-друге, при допомозі пошукових алгоритмів на графах можна визнача ти їх зв'язність. По-третє, і головне, саме на цих алгоритмах базуватимуться деякі з наступних алгоритмів, які ми надалі розглядатимемо у даному розділі.
Оцінка ефективності роботи алгоритму пошуку в глибину така сама, як і для пошуку в ширину, і становить 0(п + т).
Тестування обох алгоритмів повинно передбачати досліджен ня як зв'язних, так і незв'язних графів. У групі зв'язних графів
з* |
67 |
слід розглянути такі, у яких кількість вершин значно більша від кількості ребер, а також такі, у яких кількість ребер значно пе реважає кількість вершин. Отримані результати для обох алго ритмів необхідно порівняти щодо кількості виконаних кроків.
Завдання
1.Розробити і реалізувати у вигляді програми алгоритм пошу ку в глибину.
2.Виконати завдання 1 для графа з кількістю вершин N = 5, в якому досліджувані вершини є досяжними. Результат вико нання програми вивести у файл.
3.Виконати завдання 1 для графа з кількістю вершин N = 5, в якому досліджувані вершини є недосяжними. Результат ви конання програми вивести у файл.
4.Виконати завдання 2-3 для N = 100, вивівши результат ви конання програми у файл.
Ейлерів та гамільтонів графи
Розглянемо спочатку ейлерові графи. Під час дослідження будь-яких графів можна ставити задачу щодо наявності в них ейлерових циклів, ейлерових шляхів і взагалі доведення того, що граф є ейлеровим.
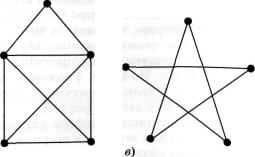
У дитинстві часто розв'язують такі головоломки: як, не відриваючи олівця від аркуша паперу, намалювати задану гео метричну фігуру (мал. 35). Виявляється, що для деяких фігур ця задача може бути розв'язана, а для деяких - ні. Це пов'яза но з тим, чи є задана фігура ейлеровим графом. Тільки у цьому разі фігуру можна намалювати.
Ейлером було доведено, що задача пошуку ейлерового шля ху має смисл тільки тоді, коли в графі є лише дві вершини з не парним степенем (k = 2) або коли всі вершини мають парний степінь (k = 0). У першому випадку будь-яка з двох вершин є
а) |
б) |
Мал. 35
68
стартовою при обході, а друга - кінцевою. У другому випадку ейлерів шлях існує і є замкненим, тобто утворює цикл, а обхід у ньому можна починати з будь-якої вершини.
Уточнимо попереднє тлумачення. Якщо у графі лише дві вер шини з непарними степенями, то це означатиме, що існуючий ейлерів шлях дасть змогу пройти через усі ребра цього графа. Якщо ж у графі є парна кількість вершин з непарним степенем, то це означає, що їх можна розбити на пари і кожна така пара дасть змогу побудувати свій ейлерів шлях у даному графі, який не охопить усі ребра, однак це зроблять усі пари разом.
На малюнку 35 зображено три різних графи, в яких при сутні ейлерові шляхи та цикли. У першому і третьому графах (мал. 35, а, в) усі вершини мають парні степені, тому існує ейлерів цикл, який можна почати у будь-якій з вершин цих графів, обійти всі їх ребра по одному разу і повернутися у стар тову вершину. Другий граф (мал. 35, б) має дві вершини зі степенем 3, тому у ньому існує не цикл, а шлях, який можна почати з будь-якої з цих двох вершин з непарним степенем, обійти всі ребра графа по одному разу і завершити обхід у другій вершині, що має непарний степінь.
Надалі будемо розглядати питання пошуку ейлерових шляхів у графі, оскільки пошук ейлерового циклу є його окремим випадком. Також зупинимося на умові, що за наяв ності непарних вершин у графі їх налічується у ньому лише дві.
Алгоритм пошуку ейлерового шляху на графі можна сфор мулювати таким чином.
1.Для кожної вершини графа обчислити степінь і перевірити наявність у ньому ейлерового шляху.
2.У разі існування ейлерового шляху в заданому графі ви значити і запам'ятати стартову вершину. Вважати її поточною.
3.Якщо існують вершини, «видимі» з поточної вершини, то продовжити пошук (п. 4). У протилежному випадку перейти до
п.5.
4.Здійснити рух по графу методом пошуку в глибину, зни щуючи дорогою всі ті ребра, через які проходимо. При цьому відповідні вершини на кожному кроці стають поточними.
5.Якщо для поточної вершини відсутні «видимі» вершини, оскільки усі ребра для неї знищені у процесі проходу по них, то запам'ятати цю вершину як складову ейлерового шляху і по вернутися до попередньої розглянутої вершини у разі, коли та ка ще існує, надавши їй статус поточної, і перейти до п. 3.
6.Процес припиняється тоді, коли буде вичерпано усі вер шини у п. 5, тобто всі ребра, якими проходили, будуть знищені. Послідовність вершин, яка була зафіксована у процесі знищен ня ребер заданого графа, і є ейлеровим шляхом, або циклом.
69
Варто детальніше розібрати і обґрунтувати коректність опи саного алгоритму. Даний алгоритм ґрунтується на двох основ них моментах:
-методом проходження по графу в глибину з поточної вер шини визначається ребро, яким можна пройти далі в наступну вершину, у результаті чого це ребро знищується;
-у разі, коли для поточної вершини відсутні ребра, якими можна пройти по графу далі, ця вершина запам'ятовується, ро биться відступ на один крок назад у послідовності розглянутих вершин, застосовується пошук у глибину для нової поточної вершини.
Перший зазначений пункт дає змогу відсікти всі можливі ребра, якими можна пройти від поточної вершини, і не вико ристовувати їх надалі в побудові наступних шляхів. Таким чи ном, проходячи по графу методом руху в глибину, ми фактич но «спалюємо за собою всі мости», щоб більше не мати змоги ними проходити.
У другому пункті, зазначеному вище, ми передбачаємо існу вання інших ходів у графі, які дають змогу нам пройти тими ребра ми, що ще залишилися. Це відбудеться, якщовиникне ситуація, коли в поточної вершини всі ребра «спалені», тобто ми вже про йшлися усіма ребрами, що проходять через цю вершину. Тому її можна включити до ейлерового шляху і продовжити пошук далі. А для цього в нас лишається тільки один вихід: повернутися на крок назад у попередню вершину, в якій побували перед цим, і знайти таку можливість, рухаючись графом з неї. Якщо і в цієї вершини всі ребра «спалені», то робимо ще один крок назад і т. д. Якщо в графі ще залишилося хоча б одне «неспалене» ребро, то це означає, що ми обов'язково знайдемо і вершину, з якої можемо цим ребром пройти, включивши його до нашого шляху.
Лише в разі відсутності ребер у заданому графі можна зроби ти висновок, що ми пройшли кожним ребром один раз і та послідовність вершин, якою проходили, і дає ейлерів шлях.
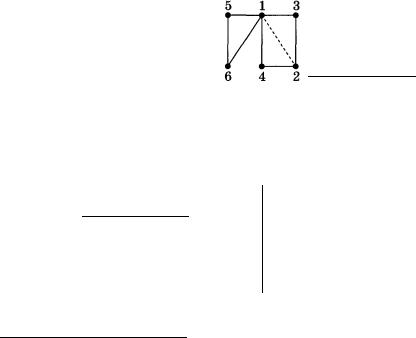
Мабуть, для більшої наочності варто розглянути конкрет ний приклад і покроково його виконати, використовуючи наве дений алгоритм. Для прикладу візьмемо вже відомий граф і відповідну йому таблицю суміжності (мал. 36, а). Аналіз цього графа показує, що в ньому існує ейлерів шлях, оскільки дві вершини 1 і 2 мають непарні степені.
Почнемо роботу нашого алгоритму, наприклад, з вершини 1 (мал. 36, а). Запишемо номер цієї вершини в першу послідов ність, де ми будемо фіксувати проходження графом.
З таблиці суміжності бачимо, що першою вершиною, у яку можемо попасти з вершини 1, є вершина 2. «Спалимо» ребро (1,2), замінивши у таблиці суміжності відповідні значення еле ментів на 0 (а[1,2] = а[2,1] = 0), і запишемо номер цієї вершини в нашу поточну послідовність (мал. 36, б). Виникає слушне за-
70
№ |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
0 |
1 |
1 |
0 |
0 |
3 |
1 |
1 |
0 |
0 |
0 |
0 |
4 |
1 |
1 |
0 |
0 |
0 |
0 |
5 |
1 |
0 |
0 |
0 |
0 |
1 |
6 |
1 |
0 |
0 |
0 |
1 |
0 |
№ |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
0 |
1 |
X |
5 |
і |
|
2 |
0 |
0 |
1 |
і |
0 |
0 |
|
3 |
1 |
1 |
0 |
о |
0 |
0 |
|
4 |
1 |
1I |
0 |
0 |
0 |
0 |
|
5 |
1 |
0 |
0 |
0 |
1 |
||
0 |
|||||||
6 |
1 |
0 |
0 |
0 |
1 |
0 |
1 2
|
|
|
|
|
|
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5 |
1 |
Я |
№ |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
5 |
1L |
3 |
№ |
1 |
2 |
3 |
4 |
5 |
6 |
||||||||
|
|
|
|
|
1 |
|
|
|
0 |
1.1 |
1 |
1 |
1 |
|
|
|
|
|
к — • |
1 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
2 |
|
|
(і |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
2 |
|
|
|
0 |
1 |
0 |
0 |
|
|
/ |
|
|
|
3 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
|
: |
|
/ |
|
|
3 |
|
|
|
0 |
0 |
0 |
0 |
||
|
|
|
|
4 |
|
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
4 |
1 |
|
0 |
0 |
0 |
0 |
||||||
|
|
і |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
6 |
|
і |
2 |
|
|||||||||||||||||||
|
|
|
5 |
1 |
n |
0 |
0 |
0 |
1 |
|
|
|
5 |
1 |
0 |
0 |
0 |
0 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
6 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
6 |
1 |
0 |
|
Q |
0 |
1 |
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
| і | 2 | з| і j : |
1 ! ' |
|
; |
, |
|
1 2 3 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
MM |
|
e) |
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5 |
1 |
|
|
|
|
|
3 |
1 |
|
|
|
|
|
||||||||||||||||
3 |
№ |
1 |
2 |
3 |
4 |
5 |
6 |
|
3 |
№ |
І |
2 |
3 |
4 |
5 |
6 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/P |
4 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
--І |
4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|||||
|
|
|
|
|
/ |
0 |
o |
0 |
0 |
I |
I |
|
|
A 2 |
/ |
|
|
0 |
|
0 |
0 |
1 |
1 |
||||||
|
|
|
|
|
2 |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
2 |
|
|
|
|
0 |
'1 |
0 |
0 |
|||||
|
|
|
|
|
3 |
0 |
<> |
о |
0' |
0 |
0 |
|
|
3 |
|
|
0 |
|
0 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5 |
|
|
1 |
0 |
0 |
0 |
0 |
1 |
|
|
|
5 |
|
1 |
0 |
0 |
0 |
0 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
6 |
|
1 |
0 |
|
0 |
0 |
1 |
0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 2 |
3 |
1 4 |
|
|
|
|
|
|
|
|
|
|
|
|
1 2 3 1 4 2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
д) |
|
|
|
|
|
|
|
|
|
|
|
|
|
є) |
|
|
|
|
|
|
|||
Мал. 36
питання: а для чого підготовлена друга послідовність і чому в неї поки що нічого не записуємо? Річ у тім, що саме в другій послідовності отримуватимемо результат, а саме ейлерів шлях, і будемо записувати туди номери тих вершин, для яких на по точний момент «спалені» вже всі ребра. А поки що такої ситу ації в нас ще не виникало.
Перейдемо до другої вершини і подивимось у другому рядку таблиці суміжності, у яку вершину можна перейти на наступ-
71
