
О.О.П / ооп / 4_кол / К курсовой / Методи побудови алгоритмів та їх аналіз / 62_201
.PDF3.Якщо із поточної вершини існує ребро у нову ще не відві дану верпіину /, то перейти до п. 4, у протилежному випадку перейти до п. 5.
4.Запам'ятати вершину /' як нову відвідану у послідовності, визначити ребро (і, j) як складову майбутнього остовного дере ва, збільшити лічильник кількості ребер в остовному дереві на 1 (count := count + 1) і визначити вершину j як поточну (і := у). Перейти до п. 3.
5.У послідовності, де зберігаються номери переглянутих вершин, перейти до передостанньої вершини і визначити її як поточну.
6.Якщо у послідовності ще є вершини, до яких можна по вернутися, і count < N - 1, то перейти до п. 3.
7.Завершити алгоритм.
Розглянемо виконання описаного алгоритму для прикладу звичайного незваженого неорієнтованого графа (мал. 48).
|
1 \ |
|
|
• 9 |
№ вер- |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
Г |
шини |
|||||||||
|
\ |
|
/ |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
ГсГ |
0 |
0 |
1 |
0 |
0 |
1 |
6. |
|
|
YА\ |
! |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
||
|
/ |
і 0 _ |
0 |
0 |
1 |
0 |
0 |
1 |
|||||
|
/ |
|
|
7 |
|
Го~ |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
J-— |
|
|
|
і |
1 |
1 |
1 |
1 |
1 |
0 |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|7 1 |
| |
| | |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
а) |
Мал. 48 |
|
Почнемо побудову остовного дерева з вершини 7. На ма люнках 49 і 50 відображені всі етапи виконання алгоритму по будови остовного дерева для заданого графа. Прокоментуємо їх. На перших двох етапах (мал. 49, а, б) нам доводиться після фіксації чергового ребра остовного дерева (у другому рядку ма люнка) повертатися у послідовності, що відображається у пер шому рядку малюнка, на крок назад, тобто до вершини з номе ром 7, оскільки ні з вершини 1, ні з вершини 2 не видно іншої вершини, окрім 7. Наступною видимою вершиною з вершини 7 є вершина 3. Запишемо її у стек (мал. 49, в).
Починаючи з вершини 3 ми можемо перейти до нової вер шини 4, а з неї до вершини 5 (мал. 50, а, в), записуючи при цьо му ребра остовного дерева у другий рядок кожного малюнка. Однак із вершини 5 неможливо побачити жодної нової верши ни, оскільки вершини 4 і 7, які видно із вершини 5, ми вже ба чили. Отже, необхідно повернутися у попередню вершину 4
92

|
|
• 2 |
|
|
|
|
•З |
|
|
6 |
|
|
|
|
|
5» |
• 4 |
• 4 |
• 4 |
7 |
1 |
|
7 2 |
7 3 |
шж |
|
(7,1)(7,2) |
1(7,1) (7,2) (7,3) |
|
а) |
|
|
б) |
в) |
|
|
|
Мал. 49 |
|
(мал. 50, в). Але і з нею відбувається те саме: вершини 3, 5 і 7 нами вже «відвідані». Тому повертаємося ще на крок назад у вершину 3. І тут спостерігається та сама ситуація. Ще один крок назад поверне нас у вершину 7. Згідно з описаним алго ритмом, і як це видно з малюнка 49, а та відповідної йому таб лиці суміжності (мал. 49, б), з вершини 7 можна побачити ще одну вершину 6. Це і є останнє ребро остовного дерева, яке ми зафіксуємо у другому рядку на малюнку 50, в.
1* |
?2 |
|
ц |
р2 |
і * |
92 |
|||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5« |
|
• 4 |
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
7 3 4 |
|
|
7 | 3 | 4 | 5 | | | |
|
|
7 6 4 5 |
|
||
(7,1)(7,2)(7,3) |
|
(7,1)(7,2)(7,3) |
|
|
(7,1)(7,2)(7,3) |
||||
(3,4) |
|
|
(3,4) |
(4,5) |
|
|
(3,4) (4,5) |
(7,6) |
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
б) |
Мал. 50 |
в) |
|
|||
|
|
|
|
|
|
|
|||
Яку реалізацію описаного алгоритму можна запропонувати мовою Pascal? За традицією спочатку розберемося, які струк тури даних необхідно для цього використати. Зрозуміло, що послідовність для запам'ятовування поточних вершин не обхідно організувати як стек. Окрім цього треба буде викорис тати множину для фіксації номерів вершин, у яких ми вже по бували і які вже використані в ребрах, що складають остовне дерево. Отже, фрагмент такої програми може бути таким:
93
t op := 1; stack[1 ] := k; {ініціалізація початку роботи алгоритму.} s := [ k j ; count := 0;
while (top > 0) and (count < n - 1) do{noi±iyK ведеться, поки стек ие порожній}
begin |
|
{і не визначені всі ребра остовного дерева.} |
||
і := 1; flag ;- false; |
|
|
{Початок пошуку з 1 -ї вершини.} |
|
while (І <= n) and not flag do |
{Пошук ведеться, поки не переглянуті} |
|||
begin |
|
|
{всі існуючі ребра М вершини.} |
|
if (d[stack[tOp], І] = 1) and not (І ІП s) |
{Якщо існує ребро, яке веде} |
|||
|
then |
|
|
{у нову вершину,} |
|
begin |
|
|
|
|
writeln(f_out, stack[top], ' ', і); |
{то виводимо його,} |
||
|
inc(count); inc(top); |
{збільшуємо кількість визначених ребер,} |
||
|
stackftop] := і; s := s + [ і ] ; |
|
{запам'ятовуємо нову вершину,} |
|
|
flag := true; |
{встановлюємо ознаку існування нового ребра.} |
||
|
end |
|
|
|
|
else Іпс(і) {У протилежному випадку переходимо до наступної вершини.} |
|||
end; |
|
|
|
|
if і > П then d e c ( t o p ) |
{Якщо у поточної вершини не існує ребер, що ведуть} |
|||
end; |
{до нових вершин, то повертаємося до попередньо переглянутої.} |
|||
Існує ще одна ідея алгоритму, який будує остовне дерево. Давайте уявимо собі, що у вершинах заданого графа розміщені ємності з різною фарбою. Якщо дати можливість фарбі з вер шини і «перетекти» існуючим ребром (і, j) у вершину/, то вва жатимемо, що вершина/ перефарбується у колір вершини і.
Отже, проаналізуємо виконання цього алгоритму на заданому графі (мал. 48, а). Із вершини 7 фарба «перетече» зразу в усі реш ту вершин, які в результаті перефарбуються у колір вершини 7, і ми отримаємо остовне дерево. Воно складатиметься з таких ре бер: (7,1), (7,2), (7,3), (7,4) (7,5), (7,6). Як бачимо, ми отримали дещо іншу відповідь, але вона також правильна. Мабуть, ви одразу впізнали в запропонованому алгоритмі пошук у ширину! У вигляді фрагмента Pascal-програми він буде таким:
head := 1; tail := 2; queue[1 ] := k; {ініціалізація початку роботи алгоритму.} s := [k]; count :=0;
While (head <> tail) and (count < П - 1) do {Пошук ведеться, поки черга не порожня}
begin |
|
{і не визначені всі ребра остовного дерева.} |
|
і := 1; flag := false; |
|
|
{Початок пошуку з 1 -ї вершини.} |
While (і <= n) and not flag do |
{Пошук ведеться, поки не переглянуті} |
||
begin |
|
|
{всі існуючі ребра ;'-ї вершини.} |
if (d[queue[head], і]=1) and not (і in s) |
{Якщо існує ребро,} |
||
then |
|
|
{яке веде у нову вершину,} |
begin |
|
|
|
writeln(f_out, queuefhead], ' ', і); |
{то виводимо його,} |
||
inc(count); queue[tail] := і; {збільшуємо кількість визначених ребер,} |
|||
inc(tail); s := S + [ і ] ; |
|
|
{запам'ятовуємо нову вершину,} |
flag := true; |
{встановлюємо ознаку існування нового ребра.} |
||
end |
|
|
|
94
I e l s e inc(i) {У протилежному випадку переходимо до наступної вершини.}
end;
if і > П t h e n inc(head) {Якщо у поточної вершини не існує ребер, що ведуть} e n d ; {до нових вершин, то повертаємося до попередньо переглянутої.}
У цьому алгоритмі може бути кілька критеріїв його виконання:
-кількість ребер остовного дерева досягла (N - 1);
-«голова» черги збіглася з її «хвостом»;
-усі вершини мають однаковий колір.
Вибір визначення цих критеріїв за автором реалізації алгорит му. Окрім цього, слід зауважити, що кожний із запропонованих алгоритмів має право на існування, а ідея з «перефарбовуванням» вершин може бути застосована в інших алгоритмах на графах.
Оцінка ефективності роботи алгоритму побудови остовного дерева очевидна: оскільки основою його є пошук у глибину, то оцінка також становитиме 0(п + т).
Під час тестування алгоритму можна розглянути графи, які самі є остовними деревами, а також майже повні графи. Це дасть змогу порівняти ефективність роботи алгоритму.
Побудова остовного дерева мінімальної довжини. Алгоритми Прима і Краскала
Цей алгоритм запропонували в кінці 50-х років XX століття незалежно один від одного два автори - Р. Прим і Дж. Краскал. Він полягає у побудові остовного дерева мінімальної довжини для зважених неорієнтованих графів, тобто таких, для кожно го ребра яких задане значення довжини (або «ваги»). Нага даємо, що матриця суміжності такого графа буде містити еле менти, які дорівнюють довжині кожного ребра.
Шукане остовне дерево будується за допомогою «жадібного» алгоритму, тобто на кожному кроці вибирається ребро з най меншою довжиною.
Алгоритми Прима і Краскала відрізняються лише на ідейно му рівні. Розглянемо їх.
Алгоритм Прима передбачає перегляд вершин заданого гра фа, починаючи з будь-якої з них, і наступне приєднання іншої вершини, до якої веде ребро з меншою «вагою». Подальше при єднання нової вершини відбувається саме за цим принципом.
Отже, алгоритм можна сформулювати так.
1. Визначити вершину і, з якої починається побудова остов ного дерева, як відвідану.
2. Якщо є невідвідані вершини, які ще не приєднані до ос товного дерева, то визначити ту з них /, до якої із множини відвіданих вершин і веде найкоротше ребро. У протилежному випадку перейти до п. 4.
95
2 шини 12 3 4 5 6 7
1 |
0 |
5 |
0 |
0 |
0 |
0 |
15 |
2 |
5 |
0 |
0 |
0 |
0 |
0 |
7 |
3 |
0 |
0 |
0 |
5 |
15 |
0 |
5 |
4 |
0 |
0 |
5 |
0 |
5 |
1 |
5 |
0 |
0 |
0 |
15 |
5 |
0 |
3 |
5 |
6 |
0 |
0 |
0 |
1 |
3 |
0 |
25 |
„ |
15 |
7 |
5 |
5 |
5 |
25 |
0 |
б)
Мал. 51
3.Додати ребро (і, j) до остовного дерева, а вершину у - до множини відвіданих вершин. Перейти до п. 3.
4.Завершити алгоритм.
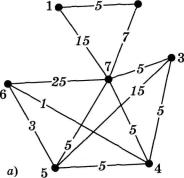
Розглянемо виконання алгоритму Прима на прикладі графа (мал. 51, а) та його матриці суміжності (мал. 51, б).
На першому кроці виконання алгоритму визначимо верши ну, з якої починається побудова остовного дерева. У нашому випадку це є вершина з номером 1. Вилучимо вершину 1 з пер шого рядка і додамо до другого як ту, що входить на початку до остовного дерева (мал. 52, а).
Звершини 1 виходить два ребра (1,2) і (1,7). Як видно з малюнка 51, а, меншим серед них є ребро (1,2). Тому на малюнку 52, бзображено саме це ребро як те, що додається на даному кроці до остовно го дерева, а вершина 2 вилучається з першого рядка (мал. 52, б) і додається до другого, як та, що вже задіяна в остовному дереві. На наступному кроці (мал. 52, в) шукаємо найближчу вершину з вер шини 2, яка ще не задіяна в остовному дереві. Такою є лише одна вершина 7, що знаходиться на відстані 7. Визначаємо нове ребро остовного дерева (2,7), додаємо вершину 7 до переліку відвіданих та вилучаємо з переліку невідвіданих. Тепер перейдемо до верши-
1* |
«2 |
|
1#—5 |
|
|
*2 |
f-5 |
|
|
|
|
f2 |
1#—5 |
|
|
^ 2 |
||
|
|
|
|
|
7 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
7 |
*3 |
|
7 |
*3 |
• |
у/ |
«3 |
|
|
|
|
|
|||||
• |
• |
|
• |
• |
|
|
• |
|
|
|
6 |
|
|
|
|
|||
6 |
|
|
6 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
5* |
# 4 |
5* |
|
|
# 4 |
5* |
|
|
|
# 4 |
5* |
|
# 4 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ЩЗ|4|5|6І7] |
J |
І8|4|5|6|7| |
| |
І3|4|5|6| |
| |
| |
І4|5|6| | |
| |
|
| |
||||||||
НІ 1 ! 1 1 1 1 |
І1І2І |
M i l l |
|1|2|7| |
І |
| |
| | |
Н І 2 І 7 І З І |
| |
! | |
|||||||||
|
а) |
|
|
б) |
|
|
|
|
в) |
|
|
|
г) |
|
|
|
||
Мал. 52
96

ни 7. Які вершини досяжні з неї та відстань до яких найменша? Та ких вершин є три: 3, 4, 5. Але за нашим алгоритмом вибереться перша з них (у порядку зростання номерів вершин, що перегляда ються). Такою вершиною стане вершина 3 і ребро (7,3) (мал. 52, г).
6 |
І5 |
|
і*г |
i^f. |
|
|
|
|
|
||
5* |
5» |
|
і |
||
|
|
|
|
|
|
5 6 |
|
|
|
г І "1 1 1 |
|
1[2|7|ЗІ4| |
|
112 |
7 3 4 6 |
| 1 | 2 | 7 | 3 | 4 | 6 | 5 | |
|
а) |
|
|
б) |
в) |
|
|
|
|
Мал. 53 |
|
|
Кроки, зображені на малюнках 53, а-в, є аналогічними і очевидними, тому додаткових коментарів не потребують. Отже, на останньому кроці (мал. 53, в) отримано остовне дере во найменшої довжини, і ознакою цього є те, що кількість невідвіданих вершин дорівнює 0.
Реалізуємо описаний і розглянутий на прикладі алгоритм Прима для побудови остовного дерева мовою Pascal:
S := [ 2 . . п ] ; |
{Визначення |
номерів непереглянутих вершин.} |
while S <> [] do |
{Продовження пошуку, поки існують непереглянуті вершини.} |
|
begin |
|
|
min := 65535; |
{Визначення початкового мінімального значення «ваги» ребра.} |
|
for І := 1 to n do |
{Перегляд усіх вершин графа.} |
|
|
{Перегляд усіх вершин, до яких можуть існувати} |
|
for j := 1 to n do |
{ребра з/'-ї вершини.} |
|
if not (і in s) and (j in s) and (d[i, j] < min) and (d[i, j] > 0) {Якщо існує} |
||
then |
|
{ребро з меншою довжиною, то} |
begin |
|
|
min := d[i, j]; I := і; r := j; |
{запам'ятати його.} |
|
end; |
|
|
if r in S |
{Якщо визначене ребро веде у нову непереглянуту вершину, то} |
|
then begin |
|
|
writeln(f out, І, ' ', г); |
{виведення ЙОГО} |
|
S := S - [ г ] ; {і виключення цієї вершини з множини непереглянутих.} end;
end;
В алгоритмі Краскала розглядаються не вершини, а ребра. Ідеєю метода є поступова побудова остовного дерева за рахунок об'єднання окремих піддерев у єдине. Спочатку до порожнього
4 Інформатика, 9-Ю кл. |
97 |

остовного дерева включається ребро з найменшою «вагою». На наступному і решті кроках додаються ребра з найменшою «ва гою» серед тих, що залишились, які ще не включені до остовно го дерева.
Алгоритм можна сформулювати так.
1. Визначити початковий стан остовного дерева як порож ній і вважати, що всі вершини утворюють N піддерев, які не мають жодного ребра. Позначити ці піддерева порядковими номерами відповідних вершин.
2.Якщо кількість ребер в остовному дереві менша за (N — 1), то серед вільних ребер заданого графа, які ще не задіяні в остов ному дереві, визначити ребро з найменшою «вагою». Таким може бути лише ребро, що належить різним піддеревам. У про тилежному випадку перейти до п. 4.
3.Додати нове ребро до остовного дерева, а вершинам, які належать двом піддеревам, що об'єднуються, і до яких нале жать вершини поточного ребра, надати значення порядкового номера одного з цих піддерев.
4.Завершити алгоритм.
Для кращого тлумачення роботи описаного алгоритму роз глянемо той самий граф, що і для алгоритму Прима (мал. 51, а). Для візуалізації покрокового виконання алгоритму Краскала на малюнках будемо відображати як послідовність ребер зада ного графа, упорядковану за зростанням їх «ваги», так і послі довність тих з них, які додаються до остовного дерева, що бу дується. Біля номерів вершин графа вказуватимемо номери піддерев, до яких вони належать, на кожному кроці виконання алгоритму.
1... 2 ,
•З,
55 *
1 |
3 |
5 |
5 |
5 |
5 |
5 |
5 |
7 |
15 |
15 |
25 |
(4,6) |
(5,6) |
(1,2) |
(3,4) |
(3,7) |
(4,5) |
(4,7) |
(5,7) |
(2,7) |
(1,7) |
(3,5) |
(6,7) |
1
(4,6)
а)
Мал. 54
98

I l l
77 |
•3, |
б! |
|
|
|
|
|
|
5b4 . |
|
'44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
5 |
5 |
5 |
|
5 |
5 |
5 |
7 |
15 |
15 |
25 |
(4,6) |
(5,6) |
(1,2) |
(3,4) |
(3,7) (4,5) (4,7) |
(5,7) |
(2,7) |
(1,7) (3,5) (6,7) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
(4,6) |
(5,6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
|
|
|
Мал. 54 (продовження) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
1.1A
7, •з,
б!
ьЧ
7 15 15 25 (4,6)|(5,6)|(1,2)|(3,4)[(3,7)|(4,5)1(4,7)1(5,7)|(2,7)|(1,7)1(3,5)|(6,7)|
1 |
3 |
5 |
|
|
|
|
|
|
|
|
|
(4,6) |
(5,6) |
(1,2) |
|
|
|
|
|
|
|
|
|
а) |
|
|
|
1 ц |
|
,2, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
б! |
|
?і |
Г |
|
|
|
|
|
|
|
|
|
, \ |
|
4, |
|
|
|
|
||
|
|
|
|
5* |
|
|
|
|
|
|
|
|
1 |
3 |
5 |
5 |
5 |
5 |
5 |
|
5 |
7 |
15 |
15 |
25 |
(4,6) |
(5,6) |
(1,2) |
(3,4) |
(3,7) |
(4,5) |
(4,7) |
|
(5,7) |
(2,7) |
(1,7) |
(3,5) |
(6,7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
5 |
5 |
|
|
|
|
|
|
|
|
|
(4,6) |
(5,6) |
(1,2) |
(3,4) |
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
Мал. 55 |
|
|
|
|
|
|
|
99

|
|
|
|
ї ї * — 5 - |
л |
|
|
|
|
|||
|
|
|
|
|
|
7,'^5~T-*34 |
|
|
|
|
||
|
|
|
|
'З |
^ |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
5> |
|
* 4 4 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
5 |
5 |
5 |
5 |
5 |
|
5 |
7 |
15 |
15 |
25 |
(4,6) |
(5,6) |
(1,2) |
(3,4) |
(3,7) |
(4,5) |
(4,7) |
(5,7) |
(2,7) |
(1,7) |
(3,5) |
(6,7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
5 |
5 |
5 |
|
|
|
|
|
|
|
|
(4,6) |
(5,6) |
(1,2) |
(3,4) |
(3,7) |
|
|
|
|
|
|
|
|
а)
їм -572,
є:
т-АгЗх
5
|
|
|
|
з |
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
4, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
5 |
5 |
5 |
5 |
5 |
5 |
7 |
15 |
15 |
25 |
(4,6) |
(5,6) |
(1,2) |
(3,4) |
(3,7) |
(4,5) |
(4,7) |
(5,7) |
(2,7) |
(1,7) |
(3,5) |
(6,7) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
5 |
5 |
5 |
7 |
|
|
|
|
|
|
(4,6) |
(5,6) |
(1,2) |
(3,4) |
(3,7) |
(2,7) |
|
|
|
|
|
|
б)
Мал. 56
Отже, на перших п'яти кроках (мал. 54, а - 56, а) ребра вклю чаються до остовного дерева підряд із упорядкованого списку всіх ребер заданого графа. Відповідно протягом включення чер гових ребер до остовного дерева номери їх вершин змінюють свою ідентифікацію щодо номера піддерева, до якого вони вклю чаються. Наприклад, на малюнку 54, а, б вершини 4, 5, 6 покроково включаються до піддерева з номером 4. А на малюнку 55, а вершини 1, 2 утворюють інше піддерево з номером 1.
Починаючи з шостого кроку (мал. 55, б) необхідно оцінюва ти доцільність включення нових ребер до остовного дерева. Ребра (4,5), (4,7), (5,7) не можуть увійти до остовного дерева. Це пов'язано з тим, що всі ці ребра відносять до одного й того самого піддерева. А піддерев на даному кроці ми маємо два:
100
0 '1
>
4,
Мал. 57
(1,2) та (3,4), (3,7), (4,6), (5,6). Отже, нам залишилося з'єднати їх одним ребром з меншою «вагою». Тому серед двох можливих ребер (1,7) «вагою» 15 і (2,7) «вагою» 7 вибираємо другий варіант (мал. 56, б).
Таким чином, на малюнку 56, б ми отримали єдине остовне піддерево, оскільки два піддерева, що існували на попередньо му кроці, об'єдналися в одне. Окрім цього всі вершини остовного дерева мають однаковий ідентифікаційний номер дерева. Підсумувавши отриманий результат, визначимо, що довжина мінімального остовного дерева для заданого графа становить 26.
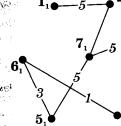
Проаналізувавши заданий граф, можна помітити, що остов не дерево, побудоване на малюнку 56, б, є не єдиним. Можливий ще такий варіант, який зображений на малюнку 57. Це дово дить той факт, що задача про визначення мінімального остовно го дерева для заданого графа дає єдину правильну відповідь тільки тоді, коли це стосується самого значення довжини цього дерева. Однак стосовно переліку ребер, що складають остовне дерево, не завжди можна отримати однозначну відповідь. Про це треба пам'ятати під час розв'язування графових задач, що передбачають отримання саме такої відповіді.
І ще одне зауваження. Ми використали під час пояснення алгоритму Краскала поняття номерної ідентифікації різних піддерев на різних кроках побудови остовного дерева, надавши номери вершинам заданого графа і надалі змінюючи значення цих номерів, якщо вершина входить до того чи іншого піддере ва. Однак це збігається з ідеєю фарбування вершин графа з по дальшим «перетіканням фарби» у вершини, які приєднуються до піддерева завдяки приєднанню відповідного їм ребра, і їх пе рефарбовуванням у новий колір. Якщо ця ідея більше до вподо би, то можна взяти її на озброєння для кращого розуміння ро боти даного алгоритму.
Саме ідею «перетікання фарби» використаємо у програмі мовою Pascal, що реалізує алгоритм Краскала:
101
