О.О.П / ооп / 4_кол / К курсовой / Методи побудови алгоритмів та їх аналіз / 42_61

Як видно з наведених фрагментів і умови задачі, відстані між містами задаються двовимірним масивом d:

array [1..100, 1..100] of word;. Наприклад, для N = 5:

0 10738

100 129 10

712046

39 4 0 5

810650

Значення d[i, і] = 0 означають, що відстань від міста і до міста і дорівнює 0.

Тестування алгоритму, що реалізує задачу про комівояжера, полягає переважно в аналізі часу його виконання при збільшен­ ні кількості міст. Також слід перевірити коректну роботу алго­ ритму для k ^ 1, тобто для випадку, коли маршрут починається і завершується з міста, порядковий номер якого відмінний від 1.

Оскільки наведений алгоритм базується на повному пере­ борі всіх можливих варіантів, то його оцінка становить 0{пХ).

Задача про розклад

Питання складання розкладу занять у навчальних закладах є дуже актуальним. Існують розроблені програми, що ре­ алізовують дану задачу і використовуються адміністрацією навчальних закладів. Але жодна з них не є такою, що повністю реалізовує найоптимальніший алгоритм. Усі вони переважно визначають пріоритети тих чи інших умов, які необхідно вра­ хувати під час складання розкладу. Наприклад, умова відсут­ ності «вікон» у розкладі викладачів, врахування побажань викладачів щодо зайнятості у ті чи інші дні тижня, уникнення потрапляння в один день занять лише з точних наук, наприклад, фізики, математики, інформатики, хімії, біології тощо.

Однак побудова алгоритму з урахуванням усіх зазначених умов і подібних до них дає змогу вирішити поставлену задачу лише на евристичному рівні, тобто знайти розв'язок, макси­ мально наближений до оптимального. Під час побудови таких алгоритмів дуже важливим є питання кількості врахованих умов та пріоритетності їх перевірки під час виконання алгорит­ му. Саме тому різні програми, що реалізовують задачу складан­ ня розкладу занять при однакових початкових даних, можуть давати різні результати. Якщо такі розв'язки не містять жод­ ної порушеної умови, то можна вважати, що вони правильні й альтернативні.

Однак у випадку, коли немає можливості перебрати всі мож­ ливі варіанти і визначити найкращий, стверджувати, що отри­ мані розв'язки є такими, дуже важко. Можливо, отримані роз-

42

в язки і справді є найкращими, а можливо, при заданих вхід­ них даних оптимального розв'язку, що враховує всі задані умо­ ви, взагалі немає.

На сьогоднішній день не існує оптимального алгоритму побу­ дови розкладу занять з урахуванням усіх можливих умов. Тому цю задачу можна віднести до класу NP. Однак розв'язати її пов­ ним перебором усіх варіантів для великої кількості вхідних да­ них - групи, викладачі, кабінети тощо - неможливо за часом.

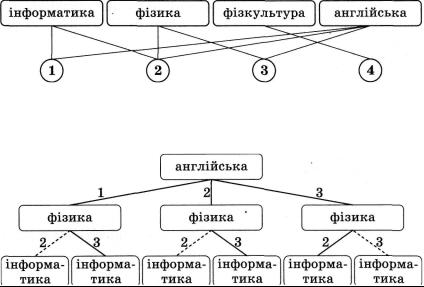
Розглянемо фрагмент задачі складання розкладу занять на один день, розглянувши 4 уроки та 4 предмети - інформатику, фізику, фізкультуру та англійську мову. Нехай відомо, що інформатика може бути лише на першому чи другому уроках, фізика - на другому або третьому, фізкультура - лише на чет­ вертому, а англійська мова - на першому, або другому, або ж на третьому уроці.

Схематично цю умову можна зобразити так (мал. 6):

Мал. 6

Наведемо схему одержання розв'язку сформульованої задачі (мал. 7), на якій суцільними лініями позначено всі можливі варіанти.

•4

Мал. 7

43

Для реалізації алгоритму у вигляді Pascal-програми створи­ мо вхідний файл tim.e_tab.in із таким вмістом:

2 12 {Кількість можливих уроків, на яких може вивчатися предмет, та номери цих уроків.}

physics 223

physical_culture

1 4 english

31 23

Для збереження вхідної інформації опишемо такі масиви:

Можна запропонувати такий алгоритм, що визначить усі можливі варіанти розкладу, враховуючи задані умови:

for і := 1 to f — 1 do begin

permutation;

j : = 1 ;

while (a[j] in lesson[j]) and (j <= n) do inc(j); if j > n then

begin

for j := 1 to n do

write(f_out, subject[a[j]], ' '); writeln(f_out);

end;

end;

Вмістом результуючого вихідного файлу time_tab.out після виконання даного алгоритму при вказаних початкових даних буде такий:

informatic physics english physicalculture informatic physicalculture english physics physics physicalculture english informatic

Як бачимо, відповідь, отримана у результаті виконання складеного алгоритму, збігається з результатами, визначени­ ми на схемі (мал. 7).

Можна зробити висновок, що існує три варіанти розкладу на один день, коли має відбутися лише чотири уроки із вказаними предметами, і всі вони відповідають заданим умовам. Оскільки ми застосували повний перебір варіантів, то можна стверджу­ вати, що отримана відповідь є єдино правильною.^

Як і попередня задача про комівояжера, наведений алгоритм за­ дачі про розклад має факторіальну оцінку ефективності роботи.

44

Типові NP задачі

Розглядаючи задачу про комівояжера, ми ставили за мету знай­ ти такий варіант об'їзду всіх міст, щоб довжина сумарного шляху була мінімальною. Така задача ідентифікується як оптимізаційна.

Однак це не єдина задача, яку ми можемо розв'язувати. Можна сформулювати задачу так: нас буде цікавити питання, чи існує розв'язок задачі, який більший або менший від деяко­ го заданого граничного значення. Такі задачі відносяться до за­ дач про прийняття рішення і ставлять за мету визначення на­ явності шуканих розв'язків.

Задача про комівояжера у варіанті прийняття рішення зво­ диться до визначення шляхів, довжина яких не перевищує за­ даної константи С. Якщо ця величина настільки велика, що пе­ ревищує суму всіх заданих довжин доріг, яку можна визначити під час введення початкових даних, то відповідь «так» можна отримати одразу без виконання самого алгоритму. Якщо ж ця величина дуже мала і менша за найменшу відстань між двома містами, то відповідь «ні» так само очевидна і також може бути отримана на кроці введення початкових даних.

У решти проміжних випадків час пошуку розв'язку значно більший і може бути порівняний з розв'язуванням оптимізаційної задачі.

Задача про розфарбовування

Нехай на дошку набито N цвяхів і до всіх них попарно прив'язані нитки. Якою мінімальною кількістю кольорів мож­ на пофарбувати головки цвяхів, щоб на кінцях кожної нитки виявилися цвяхи з різними кольорами?

Якщо міста у задачі про комівояжера і цвяхи у нашій задачі назвати «вершинами», а дороги-нитки - ребрами, то фактично обидві задачі дуже схожі своїми початковими даними. Вони відрізняються лише метою: у першій необхідно визначити мінімальну сумарну довжину ребер, а у другій - мінімальну однотипність вершин.

Якщо не шкодувати різної фарби, то всі цвяхи можна пофар­ бувати у N кольорів і наша задача буде розв'язана. Але можна поставити і складніші умови.

Якщо розв'язувати поставлену задачу як оптимізаційну, то нас цікавитиме мінімальна кількість кольорів, а якщо як зада­ чу про прийняття рішень, то - можливість розфарбування цвяхів у С кольорів або навіть і менше.

Задача про розфарбовування має практичне застосування, наприклад у такому варіанті. Якщо вершини - це назви пред­ метів у навчальному закладі, а ребра - студенти, яким вони ви-

45

кладаються, то задача про складання розкладу екзаменів поля­ гає у «фарбуванні» вершин таким чином, щоб жодному ребру не належали вершини з однаковими кольорами. У даній задачі можна ввести додаткову умову: нехай для складання всіх іспитів відводиться не більше С днів. Таким чином, наша зада­ ча перетворюється на задачу про прийняття рішення. У разі складання розкладу екзаменів за найменшу кількість днів - в оптимізаційну задачу.

Розкладання по ящиках

Нехай у нас є декілька ящиків однакового об'єму і набір де­ яких об'єктів різного розміру av а2, ..., aN. Задача оптимізації вимагатиме від нас визначення найменшої кількості ящиків, у які можна розкласти всі об'єкти, а задача про прийняття рі­ шення - чи можна розкласти всі об'єкти в С або менше ящиків.

Практичне призначення цієї задачі виникає під час запису файлів на різні диски, у разі ефективного розподілу вантажу на кораблі тощо.

Упакування рюкзака

Ускладнимо умову попередньої задачі і, крім об'єму об'єктів ах, а2, ..., aN, задамо ще й їхню вартість sv s2, ..., sN. Якщо відо­ мо, що рюкзак має вмістити об'єкти сумарною ємністю К, то задача оптимізації вимагає упакування в рюкзак таких об'єктів, вартість яких була б максимальною, об'єм дорівнював би К. Задача про прийняття рішення буде формулюватися так: чи можна досягти того, щоб сумарна вартість упакованих об'єктів не перевищувала W?

Цю задачу можна інтерпретувати ще так: чи зможемо ми до­ сягти запланованих капіталовкладень W, якщо використову­ вати різні види вкладень аг, а2, ..., aN, що передбачають відповідний прибуток sv s2, ..., sN?

Задача про планування робіт

Нехай відомий перелік N робіт, час, необхідний для їх вико­ нання tv t2, ..., tN, терміни dv d2, ..., dN, до яких ці роботи по­ винні бути виконані, та штрафирх , р2, ..., pN, які будуть накла­ дені у разі незавершення кожної роботи у визначені терміни. Задача оптимізації вимагатиме встановлення порядку робіт, що мінімізують штрафи, які накладатимуться. У задачі про прийняття рішення необхідно буде дати відповідь, чи можли­ вий порядок робіт, під час якого величина штрафу не переви­ щить заданої величини Р.

46

Завдання

1.Розробити і реалізувати у вигляді програми алгоритм задачі про комівояжера.

2.Виконати завдання 1 для N = 5, вивівши результат виконан­ ня програми у файл.

3.Виконати завдання 1 для N = 10, вивівши результат вико­ нання програми у файл.

4.Виконати завдання 1 для N = 12, вивівши результат вико­ нання програми у файл.

5.Розробити і реалізувати у вигляді програми алгоритм задачі про розклад.

6.Виконати завдання 3 для N = 5, вивівши результат виконан­ ня програми у файл.

7.Виконати завдання 3 для N = 10, вивівши результат вико­ нання програми у файл.

8.Виконати завдання 3 для N = 12, вивівши результат вико­ нання програми у файл.

9.Зробити письмовий аналіз завдань 2-4 та 6-8 щодо часу ви­ конання алгоритмів.

2.Які алгоритми відносяться до класу NP?

3.На які етапи розбивається пошук можливого розв'язку задачі, що відноситься до класу NP?

4.Якою є оцінка ефективності роботи алгоритмів, що відносяться до класу NP?

5.Які задачі можна віднести до класу NP?

6.Чому задача про комівояжера може бути віднесена до класу NP? Сформулюйте її умову і обґрунтуйте свою відповідь.

7.Опишіть алгоритм розв'язування задачі про комівояжера і зоб­ разіть його схематично.

8.Запишіть алгоритм пошуку розв'язку задачі про комівояжера мовою Pascal.

9.У чому полягає задача побудови розкладу занять?

10.Чому задачу побудови розкладу занять можна віднести до класу NP?

11.Наведіть власний приклад складання розкладу занять на один день. Зобразіть схематично пошук розв'язку поставленої задачі і обґрунтуйте його.

12.Запишіть мовою Pascal алгоритм пошуку розв'язку задачі про складання розкладу занять.

13.Які задачі можна віднести до оптимізаційних задач, а які - до за­ дач про прийняття рішення?

14.Наведіть приклади типових NP задач та сформулюйте їхні умови з урахуванням як оптимізаційної задачі, такі задачі про прийнят­ тя рішення.

47

Розділ IV

Л? • \ о VІ \ ОСНОВИ ТЕОРІЇ ГРАФІВ

оо о 0 1 1 0 1

і0 1

Теорія графів - це один із розділів математики, що дає змогу формалізувати взаємозв'язки між різноманітними видами інформації, організувати абстрактне їх представлення.

У попередньому розділі ми ознайомилися з класом NP за­ дач, для знаходження розв'язку яких необхідно було перебра­ ти всі можливі варіанти і визначити найкращий з них для оптимізаційних задач, а для задач про прийняття рішень - відповісти на запитання існування таких розв'язків.

Починаючи з даного розділу, ми будемо ознайомлюватися з оптимізаційними методами розв'язування алгоритмічних за­ дач, тобто з такими, які дають змогу знайти розв'язок задачі за найменшу кількість ітерацій. Це можливо виконати за раху­ нок відкидання на кожному проміжному кроці виконання ал­ горитму «неперспективних» варіантів, тобто таких, які у жод­ ному разі не приведуть до шуканого результату.

Знаючи різні методи розв'язування задач і коректно вико­ ристовуючи їх під час побудови алгоритмів, можна значно ско­ ротити час виконання цих алгоритмів.

Переходячи до теорії графів, слід нагадати, що ми вже мали справу з графами. Це був пошук у мережі, де сама мережа бу­ ла схематично зображена графом, у структурах даних ми пра­ цювали з деревом, яке теж є різновидом графа. У попередньо­ му розділі ознайомилися із задачею про комівояжера і задачею про розклад, які схематично також були представлені гра­ фами.

Можна також поставити запитання щодо змісту задач, які можуть базуватися на теорії графів. Не вдаючись до тлумачен­ ня мети розв'язання цих задач, про які і йтиметься у цьому розділі, наведемо лише умови їхнього вирішення. Це можуть бути такі прості і зрозумілі приклади: представлення шляхів між окремими населеними пунктами, фінансові взаємовідно­ сини між різними банками (грошові позики або борги), ауди­ торії та предмети, які можуть у них викладатися, тощо.

48

Основні поняття теорії графів

Графом називається сукупність точок (вершин) і ліній (ре- Щ бер), що їх з'єднують.

Можна також ще сказати, що графом називається сукупність точок і ліній, в якій кінці кожної лінії належать множині точок.

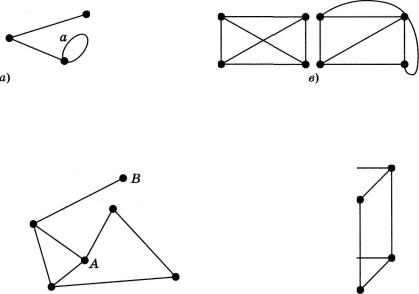
Якщо ребро з'єднує дві вершини, то кажуть, що воно інцидентне цим вершинам, а вершини, які з'єднані таким ребром, назива­ ються суміжними. Якщо кінці ребра належать одній вершині, то таке ребро називається петлею. На малюнку 8, а ребро а є петлею.

Вершини, які не належать кінцям жодного з ребер у графі, на­ зиваються ізольованими. Прикладом ізольованої вершини на малюнку 8, а є вершинаА. Граф, який складається лише з ізольо­ ваних вершин, називається нуль-графом (мал. 8, б). До речі, а чи може в графі існувати ребро без вершин? Ні, лінія, хоча б один із кінців якої не належить множині вершин графа, не є ребром.

Граф, у якому будь-яка пара вершин з'єднана ребрами, називається повним (мал. 8, в).

Am

б)

Мал. 8

Якщо всі вершини і ребра графа знаходяться в одній пло­ щині, то він називається плоским (мал. 9, а), у протилежному випадку - просторовим (мал. 9, б).

Мал. 9

Степенем вершини будемо називати число ребер, яким нале­ жить ця вершина. Або ще можна сказати, що степенем вершини називається кількість ребер, інцидентних даній вершині. Познача­ ється степінь вершини а як Р(а). Наприклад, вершинаА (мал. 9, а) має степінь 3, а вершина В - степінь 1: Р(А) = 3; Р(В) = 1.

49

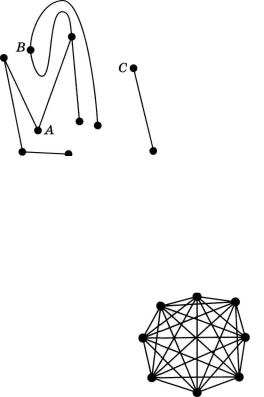
Нехай задано граф з N вершинами, які позначені а,, а2 ,..., aN. Кажуть, що існує шлях від вершини at до вершини а , якщо існує послідовність ребер, яка з'єднує вершини а та а . З ма­ люнка 10 видно, що існує шлях між вершинами А та В, оскіль­ ки існує така послідовність ребер, що їх з'єднує. У свою чергу кажуть, що вершини аі та о^ є зв'язними, якщо існує шлях від аі до аг Це означає, що вищеназвані вершини А та В є зв'язни­ ми. А от вершини А та С, а також В та С з малюнка 10 - незв'язні, оскільки не існує жодного шляху, яким можна бу­ ло б дістатися від однієї з указаних вершин до іншої.

Мал. 10

Надалі будемо називати граф зв'язним, якщо будь-яка пара його вершин зв'язна. Зрозуміло, що повний граф завжди є зв'язним, але не всякий зв'язний граф є повним. Прикладом може бути будь-який багатокутник: він зв'язний, але не пов­ ний (мал. 11, а). Але якщо у цьому багатокутнику провести всі діагоналі, то отримаємо повний зв'язний граф (мал. 11,6).

а) О б)

Мал. 11

Введемо ще один термін: циклом називається шлях, в яко­ му збігаються початкова і кінцева вершини. На малюнку 12 зображено граф, який для кожної вершини має по кілька циклів. Наприклад, для вершини 1 існує 6 циклів: (1-2, 2-5, 5-3, 3-1), (1-3, 3-7, 7-4, 4-1), (1-3, 3-5, 5-6, 6-3, 3-1), (1-2, 2-5, 5-6, 6-3, 3-1), (1-2, 2-5, 5-6, 6-3, 3-7, 7-4, 4-1), (1-3, 3-5, 5-6, 6-3, 3-7, 7-4, 4-1).

50

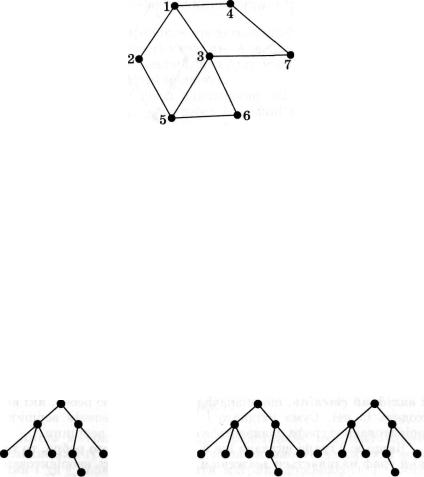
Мал. 12

Якщо цикл через кожну вершину проходить лише один раз, то такий цикл називається простим. Як видно з малюнка 12, для вершини 1 існує чотири простих цикли: (1-2, 2-5, 5-3,

3-1), (1-3, 3-7, 7-4, 4-1), (1-2, 2-5, 5-6, 6-3, 3-1), (1-2, 2-5, 5-6, 6-3, 3-7, 7-4, 4-1).

Довжиною шляху (циклу) називається кількість ребер цьо­ го шляху (циклу). На малюнку 12 для кожного вказаного цик­ лу вершини 1 неважко порахувати довжину: 4, 4, 5, 5, 7, 7.

Граф, який не має жодного циклу, називається деревом (мал. 13). Кілька дерев, які не мають спільних вершин, на­ зиваються лісом (мал. 14). Попередньо ми вже розглядали дерева як структуру даних, але обмежувалися лише випад­ ком, коли кількість нащадків кожної вершини є однаковою. Розглядаючи дерево як граф, ми будемо вирішувати більш за­ гальні задачі.

Досі ми говорили про графи, у яких ребра не мають орієн­ тації, тобто на малюнку 12 ребра 1-2 та 2-1 - не можна роз­ різнити. Однак не в усіх задачах таке обмеження нас влаш­ товуватиме. Наприклад, якщо йтиметься про географічну відстань між двома містами, то у цьому випадку нас, можли­ во, і не буде цікавити напрям руху між ними. Але якщо метою задачі є визначення економії палива на цьому відрізку шля­ ху, а один населений пункт розміщений на горі, другий - в низині, то ребра 1-2 та 2-1 будуть різними і для них не­ обхідно стрілкою вказувати напрям. Такий граф, у якому для всіх ребер вказано напрям, називається орієнтованим, або

орграфом (мал. 15).

51