О.О.П / ооп / 4_кол / К курсовой / Методи побудови алгоритмів та їх аналіз. Караванова Т.П. / 42_61

Для неорієнтованого ребра графа порядок, в якому вказую­ ться вершини, які воно з'єднує, неважливий. Для орієнтова­ ного ребра першою вказується вершина, з якої воно виходить. В орграфі також існує поняття орієнтованого шляху: це послі­ довність ребер між двома вершинами з урахуванням їхньої орієнтації. Шлях в орграфі, який є циклом, називається орієн­ тованим циклом. До речі, порівняно з неорієнтованим графом, зображеним на малюнку 12, в орієнтованому графі (мал. 15) для вершини 1 існує вже тільки два орієнтованих цикли: (1-2, 2-5, 5-3, 3-1) та (1-4, 4-7, 7-3, 3-1). Вони ж одночасно є прос­ тими. Зв'язність орієнтованого графа визначається без ураху­ вання орієнтації його ребер.

Для орієнтованих графів специфічним є визначення степе­ нів вершин. Для кожної з них окремо визначається вхідний степінь, що дорівнює кількості ребер, які входять у вершину, і вихідний степінь, що визначається кількістю ребер, які ви­ ходять із неї. Сума вхідного і вихідного степенів вершини орієнтованого графа називається степенем цієї вершини.

Якщо ж у графі вказана ще й «вага» кожного ребра, то та­ кий граф називається зваженим. Тобто існують неорієнтовані зважені графи та орієнтовані зважені графи (мал. 16). Прикла­ дом може бути задача, коли задається напрям руху дорогами між населеними пунктами та вартість перевезення ними деяко­ го вантажу.

Слід ввести поняття ще двох специфічних графів, з якими нам доведеться мати справу під час розв'язання задач. Це

ейлерів та гамільтонів графи.

Граф називається ейлеровим, якщо у ньому можна повер­ нутися в ту саму вершину, з якої ми вийшли, обійшовши кожне з ребер тільки один раз. Існують також відповідно поняття ейлерових шляхів та циклів у графі.

Граф називається гамільтоновим, якщо у ньому можна по­ вернутися в ту саму вершину, з якої ми вийшли, обійшовши кожну з вершин тільки один раз. Зрозуміло, що можна говори­ ти про існування гамільтонових шляхів та циклів у графі.

52

Способи представлення графів

Ми розглянули графічне представлення різноманітних гра­ фів, яке для нас є досить наочним. Але для складання алгорит­ му щодо розв'язання задачі, яка базується на графах, не важ­ ливі геометричні деталі малюнка.

Вважається, що граф однозначно заданий, якщо задані множини його вершин та ребер і вказані всі зв'язки цих еле­ ментів графа, тобто відомо, які вершини і якими ребрами з'єднані.

Існує два найпоширеніших способи представлення графів. Для прикладу розглянемо граф, зображений на малюнку 17, і продемонструємо на ньому ці способи.

Перший спосіб передбачає задання матриці суміжності, яка для графа з п вершинами представляється двовимірним ма­ сивом п*п.

є)

Якщо матриця суміжності представляє неорієнтований незважений граф (мал. 17, а), то за наявності суміжності вер­ шин і та J відповідні елементи матриці дорівнюють 1, тобто а[і, j] = a\j, і] = 1, а у разі відсутності ребра між вершинами і та І - 0, тобто а[і, Л = a\J, і] = 0 (мал. 17, б).

Які висновки можна зробити, проаналізувавши цю матрицю суміжності, зображену на малюнку 17, б? По-перше, для неорієнтованого графа вона є симетричною. По-друге, значення діагональних елементів дорівнюють 0, оскільки у нашому графі відсутні петлі.

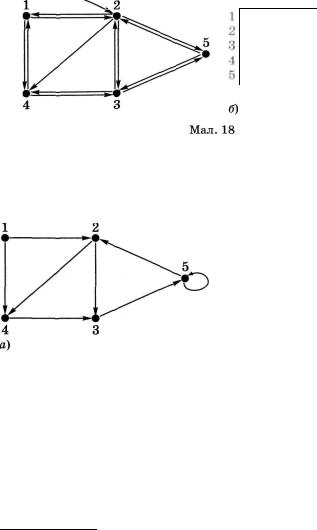
Якою ж буде матриця суміжності для інших графів? Якщо матриця суміжності описує зважений орграф, то можлива відсутність симетричності (мал. 19 а, б). У разі, коли в орграфі всі суміжні вершини мають двоорієнтовані ребра (мал. 18, а), то матриця суміжності такого графа (мал. 18, б) збігається з матрицею суміжності для графа, зображеного на малюнку 17, а.

53

в)

а)

Особливістю незваженого орграфа, у якому присутні ребрапетлі, є те, що для відповідних вершин діагональні елементи матриці суміжності не дорівнюють 0 (мал. 19, а, б). Аналогіч­ ною буде ситуація і для неорієнтованих графів.

Мал. 19

Розглянемо тепер випадок зваженого графа. Елементи матриці суміжності а[і, у], що відповідає такому графу, збігатимуться зі значеннями «ваги» ребер між вершинами і та/ (мал. 20, а, б).

Мал. 20

Другим способом представлення графа є списки суміжних вершин. У цьому разі для кожної вершини записується список суміжних вершин, який у довільному порядку містить усі суміжні з нею вершини. Графам, зображеним на малюн­ ках 17, а; 18, а; 19, а; 20, а, відповідають списки суміжних вершин, зображені на малюнках 17, в; 18, в; 19, в; 20, в.

54

Яким способом представлення заданого графа краще за все користуватися? На це запитання можна відповісти тільки сто­ совно кожного конкретного алгоритму. Звичайно, що обробля­ ти елементи матриці суміжності нам зрозуміліше і простіше. В ній ми одразу можемо дізнатися, чи є дві задані вершини суміжними, яку «вагу» має ребро, що з'єднує дві задані верши­ ни, тощо.

Однак, наприклад, для неорієнтованих графів, що не мають петель, матриця суміжності містить зайву інформацію, оскіль­ ки вона є симетричною. Якщо ж у якості опису графа обрати список суміжних вершин, то значно покращується компакт­ ність представлення інформації, однак при цьому втрачається зручність її обробки. Саме тому на самому початку ми і наголо­ сили, що спосіб представлення графа у кожному окремому ви­ падку обирається автором алгоритму згідно з умовою задачі та зі сформульованою метою її розв'язання.

Завдання

1.Розробити і реалізувати у вигляді програми алгоритм, який за заданими вхідними даними, що описують деякий граф (кількістю вершин, кількістю ребер і пар вершин, які зада­ ють ці ребра), створює відповідну матрицю суміжності.

2.Виконати завдання 1 для неорієнтованого незваженого гра­ фа, що не має петель та з кількістю вершин N = 5, вивівши результат виконання програми у файл.

3.Виконати завдання 1 для орієнтованого незваженого графа, що не має петель та з кількістю вершин N = 5, вивівши ре­ зультат виконання програми у файл.

4.Виконати завдання 1 для неорієнтованого зваженого графа, що не має петель та з кількістю вершин N = 5, вивівши ре­ зультат виконання програми у файл.

5.Виконати завдання 1 для орієнтованого зваженого графа, що має петлі та з кількістю вершин 2V = 5, вивівши результат виконання програми у файл.

6.Виконати завдання 2-5 для кількості N = 100, вивівши ре­ зультат виконання програми у файл.

7.Розробити і реалізувати у вигляді програми алгоритм, який за заданими вхідними даними, що описують деякий граф (кількістю вершин, кількістю ребер і пар вершин, які за­ дають ці ребра), створює відповідний список суміжних вер­ шин.

8.Виконати завдання 2-6 для завдання 7.

55

Пошук у ширину

Раніше ми вже розглядали різноманітні пошукові алгорит­ ми: пошук заданої інформації в одновимірному масиві, в ме­ режі, у рядку. Під час дослідження задач, що пов'язані з оброб­ кою інформації, яку можна представити у вигляді графів, та­ кож постає питання пошуку. У першу чергу - це пошук шляху від однієї заданої вершини до іншої.

Існує два підходи до здійснення такого пошуку. Розглянемо перший із них - пошук у ширину.

Як відомо, одним із найпоширеніших способів представлен­ ня графа є матриця суміжності. Саме на перегляді цієї матриці і базується метод пошуку в ширину.

Для зручнішого пояснення цього методу розглянемо конкрет­ ний приклад графа, зображеного на малюнку 21, а та відповідній йому матриці суміжності (мал. 21, б). Нехай також відомо, що необхідно визначити існування у даному графі шляху від вер­ шини 1 до вершини 7.

б)

Мал. 21

Почнемо пошук шуканої вершини 7 із заданої вершини 1 і зафіксуємо для себе цю інформацію, будуючи дерево пошуку, в якому на першому кроці нашого пошукового алгоритму є лише одна вершина 1 (мал. 22, а) та послідовність вершин, які перегля­ даються (мал. 22, б). Встановимо покажчики перегляду вершин у послідовності так: верхній вказуватиме на номер вершини, з якої ми дивимося, а нижній - на номер останньої «видимої» вершини. Відповідно на першому кроці такою вершиною є єдина вершина 1.

І ще одна інформація, яка може бути нам надалі корисною. Якщо забігти наперед і розглянути заданий граф (мал. 21, а), то можна помітити, що вершину з номером 1 знову побачимо, коли перейдемо до перегляду вершин 2, 3 та 4. Але повертатися у неї немає сенсу, оскільки при цьому ми «зациклимося» і бу­ демо крутитися на одному і тому самому місці. Тому варто за­ пам'ятовувати номери вершин, у яких ми вже побували, для

56

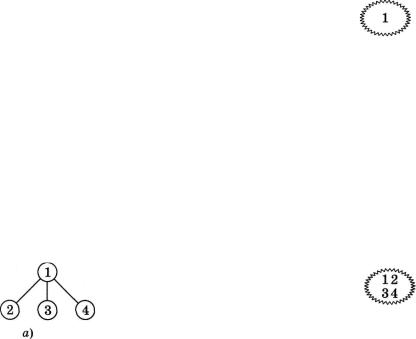
того, щоб виключити їх надалі з перегляду. Яким чином мож­ на реалізувати такий захист? Можна запропонувати два спосо­ би: перший - проглядати послідовність переглянутих вершин (мал. 22, б), другий - використати множину для їх фіксації (мал. 22, в). Який з них ефективніший? Якщо кількість вер­ шин невелика, то раціональніше скористатися множиною, як­ що ж вона більша за 256 - то переглядом послідовності. Але у цьому разі інформацію про заданий граф необхідно представля­ ти у вигляді списку суміжних вершин.

4

®

U

Мал. 22

Продовжимо пошук вершини 7. З малюнка 21, а видно, що з вершини 1 ми бачимо вершини 2, 3 і 4. Ту саму інформацію ми можемо отримати і з таблиці суміжності (мал. 21, б), пере­ глянувши рядок, що відповідає номеру вершини, з якої ми дивимося, тобто перший рядок таблиці. Давайте зафіксуємо цю інформацію у дереві пошуку (мал. 23, а), у послідовності номерів вершин, які ми переглянули (1) і які ми бачимо (2, 3, 4) (мал. 23, в). Серед них поки що шуканої вершини 7 немає.

Мал. 23

Для подальшого пошуку перейдемо до однієї з нових вершин, які ми побачили. Це вершини 2, 3 і 4. У нашій послідовності (мал. 23, б) першою записана вершина 2, тому й перейдемо до неї. Які вершини ми бачимо з вершини 2 (мал. 21, а)? Це верши­ ни 1, 3, 5 і 6. Цю саму інформацію можна отримати з другого рядка таблиці суміжності (мал. 21,6). Однак лише вершини 5 і 6 є новими, а вершини 1 і 3 ми вже бачили на попередніх кроках нашого алгоритму. Доповнимо дерево пошуку (мал. 24, а), по­ слідовність переглянутих і «видимих» вершин (мал. 24, б) та множину (мал. 24, в) новою інформацією.

57

Мал. 24

Чи завершили ми наш пошук? Зрозуміло, що ні, оскільки ні

удереві пошуку, ні у послідовності ми ще не дісталися шуканої вершини 7. Тому переходимо у послідовності вершин до на­ ступної «побаченої» вершини 3. Тепер її можна буде назвати не лише «побаченою», але ще й «переглянутою». Згідно із зобра­ женням графа і відповідної йому таблиці суміжності з вершини

Зми бачимо вершини 1, 2, 4 і 5. Але вони не є новими, тому ми їх не фіксуємо ні у дереві пошуку, ні у послідовності вершин, ні

умножині (мал. 25, а, б, в).

0-

Г1 І 2 1 3 | 4 ГбТб

-о-

Мал. 25

Переходимо до наступної вершини у послідовності, якою є вершина 4. Звідси ми бачимо вершини 1 і 3. Але і ці вершини вже є «побаченими», тому у нашому алгоритмі змінюється лише вершина, яку ми переглядаємо наступною. Такою верши­ ною є вершина з номером 4, тобто наступна у нашій послідов­ ності «переглянутих» і «видимих» вершин (мал. 26, б). З вер­ шини 4 ми знову-таки нічого нового не побачимо, оскільки вершини 1 та 3 ми вже бачили раніше. Інформація на малюн­ ках 26, а та 26, в залишилася незмінною.

58

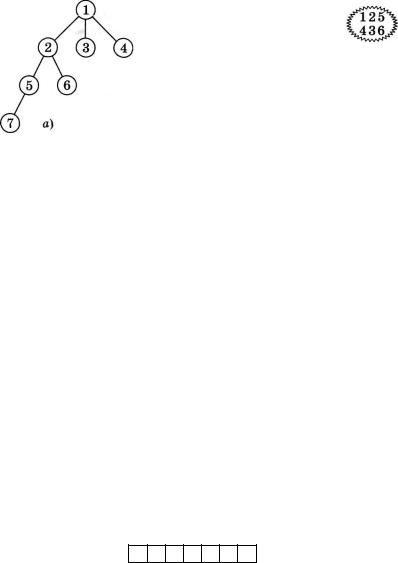
Продовжуючи логіку нашого алгоритму, переходимо до вер­ шини 5 - наступної у нашій послідовності (мал. 27, б). З верши­ ни 5 ми бачимо вершини 2, 3, 7. Перші дві з цих вершин уже бу­ ли переглянуті, а от вершина 7 не тільки нова, але й ще шука­ на. Тому алгоритм можна вважати завершеним, а відповідь на поставлене на початку запитання буде такою: «У заданому графі вершина 7 є досяжною з вершини 1».

й

Мал. 27

Проаналізуємо описаний алгоритм з точки зору його ре­ алізації у вигляді програми. Як було вже сказано вище, інфор­ мація про граф міститиметься у таблиці суміжності або у списку суміжності. Інформація про «переглянуті» і «побачені» верши­ ни - в одновимірному масиві. Алгоритм обробки цього масиву відповідає роботі зі структурою даних «черга», де «голова» чер­ ги вказує на поточну вершину, з якої ми дивимося далі, а «хвіст» вказує на останню видиму вершину. Під час виконання алгоритму «голова» переміщується вправо на нову вершину, в яку ми переходимо для подальшого перегляду нових вершин, а «хвіст» також переміщується вправо одночасно з дописуван­ ням нових видимих вершин.

Тепер ми можемо проаналізувати умови завершення роботи алгоритму пошуку в ширину. Таких випадків є два: шукана вершина знайдена і відомий шлях до неї, або шукана вершина є недосяжною і шлях до неї відсутній.

Ми розглянули саме перший випадок пошуку вершини в графі, коли шукана вершина 7 є досяжною із заданої верши­ ни 1. Шлях від вершини 1 до вершини 7 присутній у черзі, але без додаткової інформації він дещо прихований. Для отриман­ ня цього шляху необхідно запам'ятовувати також і номери вер­ шин, з яких ми побачили кожну наступну вершину. На малюн­ ку 28 ця інформація позначена індексами для кожної поточної вершини, записаної у чергу.

1„ 2і Зі 4і 52 62 75

Мал. 28

59

Другий випадок може бути розтлумачений так: «голова» черги досягнула її «хвоста», а серед нових «побачених» вершин так і не з'явилася шукана. Це означає, що ми переглянули всі досяжні вершини графа, але не змогли дістатися до шуканої.

Підіб'ємо підсумок наших міркувань і опишемо алгоритм пошуку в ширину в словесній формі.

1.Вказати номер вершини k, з якої починається пошук за­ даної шуканої вершини І.

2.Почати перегляд вершин заданого графа з вершини k, за­ писавши її в чергу: і := k. Одночасно ця вершина є і останньою «побаченою» вершиною: j := k.

3.Зафіксувати всі нові вершини, які можна побачити з вер­ шини і, в порядку зростання їх номерів, записуючи їх у чергу і збільшуючи при цьому на кожному кроці індекс «хвоста» чер­

ги ; на 1 (j := j + 1).

4.Якщо серед нових «побачених» вершин, записаних у чер­ гу, є шукана вершина, то перейти до п. 8.

5.Для переходу до перегляду наступної «побаченої» верши­ ни збільшити значення індексу «голови» черги і(і:=і + 1).

6.Якщо значення індексу «голови» черги і збіжиться зі зна­ ченням індексу його «хвоста» ;', то перейти до п.10.

7.Перейти до перегляду наступної «побаченої» вершини і (п. 3).

8.Вивести інформацію про те, що шукану вершину І досяг­ нуто і шлях до неї від вершини k існує.

9.Перейти до п. 11.

10.Вивести інформацію про те, що шукана вершина І недо­ сяжна від вершини k і шлях до неї відсутній.

11.Завершити алгоритм.

Перейдемо до реалізації описаного алгоритму у вигляді фрагмента Pascal-програми:

ІПС(І) {Перехід до наступного елемента к-го рядка таблиці суміжності.}

end;

60

if flag t h e n write(f_OUt, 'YES') {Інформація про те, що знайдено шукану вершину.} {Інформація про те, що} e l s e Wlite(f_OUt, 'NO'); {не знайдено шукану вершину.}

Для реалізації алгоритму, що визначає шлях від заданої до шуканої вершини, необхідно зробити корективи.

Опис одновимірного масиву, який реалізує структуру даних «черги», можна запропонувати такий:

a: array[1..100] of record

top, prev: byte; end;

Початкові значення параметрів «черги» будуть такими: head := 1; tail := 2; a[l].top := k; a[i].prev := 0;

а фрагмент програми, що поповнює «чергу» новими «видими­ ми» вершинами, такий:

if (d[a[head].top, і] = 1) and not (і in s) then

begin

a[tail].top := i; a[tail].prev := head; inc(tail); s := s + [i];

if і = I then flag := true; end;

Для виведення інформації про існуючий шлях від заданої вершини до шуканої можна запропонувати такий фрагмент програми мовою Pascal:

write(f_OUt, a[tail].top); {Виведення номера вершини, що є початком шляху.} end

else write(f_out, 'NO');

Підіб'ємо остаточний підсумок розглянутого методу. По-пер­ ше, тепер зрозуміло, чому цей метод носить назву «пошук у ши­ рину». Адже дійсно ми ведемо пошук шуканої вершини, роз­ глядаючи на кожному новому кроці одночасно всі нові вершини по рядках таблиці суміжностей, які ще не бачили. По-друге, можна зробити висновок, що метод пошуку в ширину дає най-

61