
О.О.П / ооп / 4_кол / К курсовой / Методи побудови алгоритмів та їх аналіз. Караванова Т.П. / 252_337
.PDF
Визначення площі багатокутника
Найчастіше в обчислювальній геометрії багатокутники за даються координатами своїх вершин. Порядок задання цих вершин повинен бути обумовлений обходом цього багатокутни ка за годинниковою або проти годинникової стрілки. Напрям обходу в даному разі не має значення, оскільки йтиметься про площі цих фігур.
Площу трикутника, прямокутника, ромба можна визначити за відомими з математики формулами. А як бути, коли задано багатокутник на площині як опуклий, так і неопуклий? Коли опуклий, його можна розбити на трикутники, провівши діаго налі з будь-якої вершини до всіх решти, не суміжних з нею, визначити їхні площі, наприклад за формулою Герона, і знай ти їхню суму (мал. 143, а). А якщо він неопуклий, то такий підхід до розв'язання поставленої задачі не дасть позитивного результату (мал. 143, б). Спробуємо розв'язати задачу про ви значення площі багатокутника за допомогою тих ідей, які вже були розглянуті вище.
а) |
б) |
Мал. 143
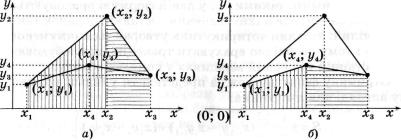
Розглянемо довільний чотирикутник з вершинами у точках (Хі, ух), (х2; у2), (х3; у3), (*4; у4) (мал. 144). Якщо з кожної вер шини опустити вертикальні лінії на вісь Ох, то отримаємо точ ки (х\; 0), (х2; 0), (х3; 0), (х4; 0). Неважко помітити, що шукану площу заданого чотирикутника можна отримати так: від суми площ трапецій, зображених на малюнку 144, а, відняти суму площ трапецій, зображених на малюнку 144, б.
А чи достатньо для цього інформації про заданий чотирикут ник у вигляді координат його вершин? Виявляється, що так. Ос нови трапеції, що утворюються точками (хй; 0), (хх; ух), (х2; у2), (х2; 0) (мал. 144, а), мають довжини ух та у2, а висота дорівнює (х2 - хх). Площу цієї трапеції можна буде визначити за форму-
(и, +у9)(Хо-х,) |
» |
. |
. . . |
|||
лою —J |
|
— |
|
***, |
Аналогічно |
представимо і площі інших |
|
|
|||||
252
(x„; y2)
(x„; ya)
(0;0J
Мал. 144
трьох трапецій (мал. 144): |
(Уа+УаУ(х8-хі) (Уя+У*)(х4-ха) |
||
2 |
|||
|
|
||
(У4+УІ)(ХІ-ХІ) |
Варто обговорити принцип запису цих формул. |
||
|
|||
с
Як бачимо, у них використана певна послідовність розгляду вершин заданого чотирикутника: в порядку їх обходу за годин никовою стрілкою. Перші два вирази даватимуть у результаті обчислення додатні значення (х2 - хг > 0, х3 - х2 > 0), а другі два - від'ємні (х4 - х3 < 0, хг - х4 < 0). Отже, немає необхідності в інформації про те, площі яких трапецій необхідно додавати, а яких - віднімати. Всі їх треба лише додавати - це обумовлено порядком обходу вершин заданого багатокутника.
Однак тут все-таки є одна особливість. У нашому прикладі обхід виконується за годинниковою стрілкою і сума додатних площ більша за суму від'ємних, у результаті чого буде отрима но додатний результат, що і є шуканою площею заданого ба гатокутника. А якщо обхід робити у зворотному порядку, то ре зультат отримається правильний, але від'ємний. Напрошуєть ся висновок: оскільки в задачах переважно невідомо, у якому порядку задаються веріпини багатокутника, то відповіддю буде модуль обчисленого результату.
Виконавши алгебраїчні перетворення, отримаємо:
±((Уі+У2)(Х2-Хі) , (Уі+Уз)(Х3-Х2) J (У8 +У4)(*4-*з) , (У4+Уі)(хі-Х4)) =
= ± 2 К*гУі -*i%)+(хзУ2 - хгуг ) + (хіу3-х3у4) + (xty4 - хіу1 ))\
Чи не схожі доданки отриманої формули з виразами, що ви значають напрям повороту при обході багатокутника від кожної вершини {хі + j; г/. + -^ до його попередньої вершини (xt; yt)? Усі,
1 + означає, що коли отримується додатний результат, то його знак не змінюється, а коли від'ємний, то його знак змінюється на протилежний. Така операція аналогічна визначенню модуля числа.
253
окрім останнього, такими і є, у даній формулі враховуються не тільки їх знаки, але й їхні значення. Останній доданок так само зрозумілий: заданий чотирикутник утворюється замкненою ла маною і тому необхідно врахувати трапецію, що побудована на його останній та першій вершинах у порядку обходу.
Отриману формулу можна представити у більш компактно му вигляді для я-кутника:
1 f"'1 |
л |
& V 1=1 |
; |
Використовуючи запис у векторному вигляді, наведену фор мулу можна ще представити так:
!/V.
S = ±2- І УМУІ + УіУп
Переходячи до мови програмування, представимо фрагмент Pascal-програми, що обчислює площу багатокутника, який за даний координатами своїх вершин у порядку їх обходу:
read(f _ in, п); |
{Введення кількості вершин багатокутника.} |
f o r і := 1 to П do |
{Введення координат вершин багатокутника.} |
read(f_in, х[і], у[і]);
s:=x[1]*y[n]-x[n]*y[1]; {Визначення початкового значення результату.}
for і := 1 to n - 1 do {Покрокове визначення площі багатокутника.}
s := s + (x[i + 1] * y[i] - x[i] * y[i + 1]);
writeln(f_OUt, abs(s)/2:0:5); |
{Виведення остаточного результату.} |
Оцінка роботи описаного алгоритму зрозуміла: для визна чення площі заданого багатокутника необхідно послідовно двічі розглянути всі його п вершин. Тому оцінка ефективності запропонованого алгоритму 0{п).
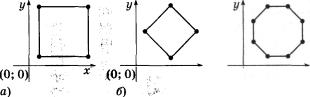
При тестуванні алгоритму обчислення площі багатокутни ка необхідно передбачити різні види багатокутників - опуклі, неопуклі, з невеликою кількістю вершин та з кількістю вер шин, близькою до 100. Для зручності перевірки правильності роботи алгоритму можна задати правильні багатокутники (мал. 145, в), починаючи з квадратів, площі яких неважко ви рахувати вручну (мал. 145, а, б). У якості неопуклого багато кутника можна дослідити багатокутник, сторони якого зуб часті (мал. 145, г), або подібні до такого.
|
у\ |
г/АЛЛ/И |
|
|
W V W 1 |
х (0; 0) |
х (0; 0) |
х |
в) |
г) |
|
Мал. 145 |
|
|
254
Цікавою є задача визначення напряму обходу опуклого багатокутника, заданого координатами своїх вершин. Відпо відь випливає із визначення напряму повороту при переході від точки (xt; yt) до точки (л;;.; і/;.).
А чи можна впорядкувати задані в довільному порядку вер шини опуклого багатокутника за певним напрямом його обхо ду? Так, можна, якщо підібрати таку їх послідовність, щоб знак виразу (xtyl+1 - xi+lyt) для будь-якої пари сусідніх вершин (xt; yt) і (хі+1; уі+і) не мінявся на протилежний.
Завдання
1.Розробити та реалізувати у вигляді програми алгоритм ви значення коефіцієнтів загального рівняння прямої, заданої двома точками (дсх; уг) і (х2; у2).
2.Розробити та реалізувати у вигляді програми алгоритм визна чення довжини відрізка, заданого двома точками (д:1; уг) і (х2; у2).
3.Розробити та реалізувати у вигляді програми алгоритм ви значення взаємного розміщення двох точок (Xj; у2) та (х2; у2).
4.Розробити та реалізувати у вигляді програми алгоритм ви значення взаємного розміщення двох прямих, кожна з яких задана координатами двох точок.
5.Розробити та реалізувати у вигляді програми алгоритм ви значення взаємного розміщення двох точок і прямої, також заданої координатами двох точок.
6.Розробити та реалізувати у вигляді програми алгоритм ви значення взаємного розміщення точки і відрізка.
7.Розробити та реалізувати у вигляді програми алгоритм ви
значення напряму повороту від заданої точки {хг; уг) до ін шої заданої точки (х2; у2) у разі, коли спостереження ведеть ся з початку координат (0; 0).
8.Розробити та реалізувати у вигляді програми алгоритм ви
значення напряму повороту від заданої точки (лгх; у^) до ін шої заданої точки (х2; у2) у разі, коли спостереження ведеть ся з довільної точки (х0; у0).
9.Розробити та реалізувати у вигляді програми алгоритм ви значення площі багатокутника, заданого координатами вер шин у порядку їх обходу.
10.Виконати завдання 9 для опуклого багатокутника з кількістю вершин N < 10. Результат виконання програми вивести у файл.
11.Виконати завдання 9 для неопуклого багатокутника з кількістю вершин N ^ 10. Результат виконання програми вивести у файл.
12.Виконати завдання 9 для опуклого багатокутника з кіль кістю вершин N ^ 100. Результат виконання програми ви вести у файл.
255

13. Виконати завдання 9 для неопуклого багатокутника з кількістю вершин N < 100. Результат виконання програми вивести у файл.
/Запитання для самоконтролю
І1. Які задачі розв'язує обчислювальна геометрія?
2.Як задається розміщення точки на площині і як вирішити питан
ня точності такого задання?
3.Як можна однозначно задати пряму на площині?
4.Як задається відрізок прямої на площині і визначається його довжина?
5.Яким може бути взаємне розміщення двох точок на площині?
6.Як визначити взаємне розміщення двох прямих на площині?
7.Яким може бути взаємне розміщення точок і прямої на площині?
8.Яким є аналіз взаємного розміщення точки і відрізка?
9.Як визначити напрям повороту при переміщенні від однієї точки до іншої, якщо спостереження відбувається з початку координат (0; 0)? Обґрунтуйте свою відповідь.
10.Як визначити напрям повороту при переміщенні від однієї точки до іншої, якщо спостереження відбувається з будь-якої іншої довільної точки? Обґрунтуйте свою відповідь.
11.У чому полягає метод визначення площі багатокутника?
12.Якою є оцінка запропонованого методу визначення площі багатокутника?
13.Наведіть фрагмент реалізації алгоритму визначення площі багатокутника мовою програмування.
Перетин відрізків
Нехай на площині задані два відрізки відповідними коорди
натами своїх кінців (Xp i/j), (х2; у2) і |
(х3; у3 ), (х4; у4). їхнє |
взаємне розміщення може бути різним. |
Усі ці випадки зобра |
жено на малюнку 146, де для більшої наочності кінці заданих відрізків позначено відповідно рх, р2 ір3, р4. Розглянемо всі ці випадки і спробуємо визначити певну закономірність, яка буде слугувати ознакою перетину досліджуваних відрізків.
Проаналізувавши малюнок 146, а, можна зробити наступ ний висновок.
Якщо з точки р1 дивитися спочатку у точку р2, що є проти лежним кінцем цього відрізка, а потім перевести погляд у точ
ку ps, то при цьому буде виконано поворот проти годинникової |
||||
стрілки. |
Ознакою |
такого повороту |
буде |
виконання умови |
(Рг _ $і) х |
(Рз ~ Pi) > |
0- Якщо, дивлячись із точки рх у точку р2, |
||
перевести погляд у точку р4, то при цьому буде виконано пово |
||||
рот за годинниковою стрілкою: (р2 - рг) х (р4 |
- />1) < 0. Остаточ |
|||
ний висновок буде таким: якщо кінцір3 \р4 |
відрізка лежать по |
|||
різні боки від |
а з кінцями р1 |
і р2, то при цьому вико |
||
нується256 умова [(рвідрізк- ) х (р -/>!>] • [(р |
~Рі) х (р ~Рі)] < °- |
|||
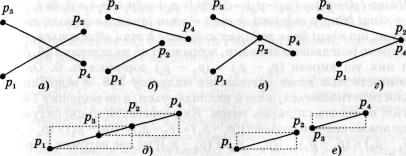
Мал. 146
Однак отриманої залежності замало для остаточного виснов ку про те, що задані відрізки перетинаються. Така сама ситу ація повинна мати місце і для відрізка з кінцями р3 і р 4 : якщо дивитимемося із точки р3 у точку Рі, то при переведенні погля ду в точки р1 їр2 поворот здійснюватиметься у різні боки. Від повідно до цього умову виконання такого взаємного розміщен ня відрізків запишемо так:
[(Р4 ~Ра) х (Рі -Р8 )] * [0>4 ~Рз) х (Р2 -МУ\ < °- А тепер вже можна сформулювати остаточний висновок.
Два задані відрізки з кінцями у точках pvp2 ір3,р4 перети наються тільки в разі, коли виконуються такі дві умови:
[(р2 -Рі) * (р8 ~Рі>) • [(?2 - Р і ) х о>4 -Рі)] < °;
Ш -Ря) х (Рі -Р8 )1 • [СР4 -Рв) х (Ра - Рз)1 < °- Зрозуміло, що якщо два задані відрізки не перетинаються
(мал. 146, б), то одна із зазначених вище умов не виконується. Цікавими для аналізу є інші випадки взаємного розміщення двох заданих відрізків і умови їх визначення, які ми далі й роз
глянемо.
На малюнку 146, в представлено випадок, коли кінець одно го відрізка розміщений на іншому відрізку. Як бачимо, умова
[(Р2 ~Рі) х (Рз ~Рі)3 • Е(Рг ~Рі) х (Р4 ~Рі)} < ° виконується, однак якщо дивитися із точки р3 у точку р4, а потім у точку р2, то (Р4 - Рз) х (Р2 _ Рз) = ®' Таким чином, друга із зазначених вище умов у даному разі буде такою:
[(Р4 -Р») х (Рі "Рз)] * [(Р4 "Рз> х (Р2 _ Рз)] = °-
Якщо лише один із виразів (Pj-pt) х (pk ~Pt) дорівнює 0, де і, І - кінці одного відрізка, k - один із кінців іншого, то це означає, що кінець k одного відрізка лежить усередині другого відрізка.
Розглянемо випадок, коли по одному з кінців кожного з двох заданих відрізків збігаються. Саме така ситуація зображена на ма люнку 146, г. Зрозуміло, що у такому разі у кожному з виразів [(Р2 - Рі) х (Рз - Рі)] * [(Р2 - Рі) х (Р4 " Рі)] і
[(Р4 - Р 8 ) х (Рі "Рз)1 • [(Р4 "Рз) х (Рг "Рз)] лише один із множників набуває значення 0.
9 Інформатика, 9-10 о. |
257 |
Якщо (pj -pt) x (pk -Pi)=0i (pl -pk) x (Pi -pj = 0, де і, j та h,l- кінці одного відрізка, k та і - один із кінців іншого, то це
означає, що кінці двох заданих відрізків k та і збігаються.
Окремо розглянемо випадки, зображені на малюнках 146, діє. Для них усі вирази (ру. - pt) х (pk - pt) дорівнюють 0. Однак відмінність між ними суттєва: на малюнку 146, д відрізки не тільки перетинаються, а ще й накладаються, а на малюнку 146, є взагалі не мають спільних точок. Як розрізнити ці дві ситуації, якщо аналіз значень виразів [(р2 -р^) х (р3 -p-J] • [(р2 -рг ) х (р4 -pj)]
і [(Р4 ~Рз) * ІРі -Рзїї - [(^4 ~Рз> х (Рг _ Рз)] не Да є вагомих резуль татів?
На малюнках, що розглядаються, вже є підказка: необхідно розглянути прямокутники мінімальної площі, що вміщують у собі задані відрізки. Якщо ці прямокутники перетинаються, то і відрізки мають спільні точки, тобто накладаються. Для пе ревірки цієї умови достатньо мати інформацію про координати кінців цих відрізків. Але перш ніж записати необхідну умову,
треба ввести деякі нові позначення. |
|
|
|
|
||||
|
|
|
Нехай |
х\ |
- |
тіп{х^, |
х2), |
|
( * і! |
Уі). |
х'2 |
= тах(хх; |
х2), |
у\ |
= тіпіу^, |
у2), |
|
у'2 |
= тах{ух; у2) (мал. 147). Тоді |
|||||||
|
|
|||||||
|
|
умовою перетину двох прямокут |
||||||
|
|
ників мінімальної |
площі, |
що |
||||
|
:.;!:і |
-Лх^Уг) вміщують дві задані прямі, |
буде |
|||||
|
|
така: |
|
|
|
|
||
|
|
Мал. 147 |
(Х'2 >= Х'3) and (х'4 |
>= х'Л and |
||||
|
|
|
(y'2>=y'3)and(y'i>=y\). |
|
||||
|
Саме ця умова виконується для відрізків, зображених на ма |
|||||||
люнку 146, д, і не виконується для відрізків на малюнку 146, є. Підіб'ємо остаточний підсумок усіх наведених міркувань. 1. Якщо задача вимагає визначення, чи перетинаються за
дані два відрізки в одній точці, яка одночасно не є жодним з їхніх кінців, то достатньо перевірити такі дві умови:
[(Р2 -Рі) х (Рг " P i ) ! • КРа ~Рд х Щ ~Рд) < °! [ІРІ -Р3) х (Рі -Рз)1 * [(Р4 ~Рз) х (Рг ~Рз)1 < °-
2. Якщо в задачі можливий перетин відрізків з накладан ням їхніх кінців (мал. 146, в, г), то необхідно провести деталь ніший аналіз щодо нульових значень виразів (р -pt) х (pk - pt)- 3. Якщо у сформульованій задачі ставиться запитання про визначення наявності спільних точок (не обов'язково однієї) для двох заданих відрізків, то спочатку достатньо перевірити виконан ня умови (х'2 >= х'3) and (х'4 >= х\) and (у'2 >= у'3) and (у\ >= у\).
У разі її невиконання можна зразу давати негативну відповідь. У випадку позитивної відповіді і для того, щоб виключити варіант, зображений на малюнку 146, б, необхідно перевірити ще виконання умов:
258
[(p2 -Pi) x (p3 -РіУ\ • [(P2 -Pi)x (P4 -Pi)l * o; [(P4 - Ps> X (Pi - РЗ>] • f(P4 - Рз) X (P2 - Рз)] * °-
Наведемо приклад фрагмента Pascal-програми, що аналізує перетин двох заданих відрізків:
X 1 := min(p[1].x, р[2].х); х_2 := тах(р[1].х, р[2].х); {Обчислення координат}
у_1 |
:= min(p[1].y, р[2].у); у_2 |
:= тах(р[1].у, р[2].у); |
{вершин охоплюючих} |
х_3 |
:= тіп(р[3].х, р[4].х); х_4 |
:= тах(р[3].х, р[4].х); |
{прямокутників.} |
у_3 := min(p[3].y, р[4].у); у_4 := тах(р[3].у, р[4].у); |
|
||
|
{Перевірка умови перетину охоплюючих прямокутників.} |
||
if (х_2 >= х_3) and (х_4 >= х_1) and (у_2 >= у_3) and (у_4 >= у_1) {Якщо вони} then {перетинаються, то обчислення параметрів для перевірки умови їх перетину.}
begin
р_1_23:=(р[2].х-р[1].хГ(р[3].у-р[1].у)(р[3].х-р[1].хГ(р[2].у-р[1].у); р_1_24:=(р[2].х-р[1].хГ(р[4].у-р[1].у)(р[4].х-р[1].хПр[2].у-р[1].у); Р_3_41:=(р[4].х-р[3].х)*(р[1].у-р[3].у)(р[1].х-р[3].х)*(р[4].у-р[3].у); р_3_42 := (р[4].х- р[3].хГ(р[2].у- р[3].у) (р[2].х- р[3].х)*(р[4].у- р[3].у); if (PJ_23 * р_1_24 <= 0) and (р_3_41 * р_3_42 <= 0) {Перевіркаумови}
then writeln(f_out, 'Yes crossing') |
{перетину відрізків.} |
else writeln(f out, 'Not crossing'); |
|
end |
|
else writeln(f_out, 'Not crossing'); |
|
Поставлену на початку задачу про визначення факту пере тину двох заданих відрізків можна було б розв'язувати інакше. Для цього за основу слід взяти розв'язання системи двох ліній них рівнянь, що описують прямі, яким відповідають задані відрізки. Наведемо послідовність відповідних дій.
1.Визначити коефіцієнти загальних рівнянь прямих av bv
с1 і а2, Ь2, с2, яким належать задані відрізки, враховуючи коор
динати їх кінців.
2. Розв'язати систему лінійних рівнянь
{a1x + bly + cl =0; \а2х + Ь2у + с2=0
і визначити, чи існує її розв'язок (х; у). Аналіз отриманого розв'язку дасть відповідь на запитання: чи існує єдиний розв'язок або ж таких розв'язків безліч?
3. Якщо існує єдиний розв'язок досліджуваної системи лінійних рівнянь {х; у), то залишається перевірити, чи нале жить ця точка обом відрізкам:
(х\ <= х) and (х <= х'2) and (у\ <= у) and (у <= у'2) and (х'3 <= х) and (х <= х\) and (у'3 <= у) and (у <= у\).
4. У разі, коли система двох рівнянь має безліч розв'язків, це означає, що досліджувані відрізки можуть мати спільні точ ки. Тому для отримання позитивної відповіді на поставлене у
9* |
259 |

сформульованій задачі запитання щодо перетину двох заданих відрізків доцільною є перевірка виконання додаткової умови:
(х'2 >= х'3) and (х\ >= х\) and (у'2 >= у'3) and {у\ >= у\).
Як видно з другого алгоритму визначення перетину двох за даних відрізків координатами своїх кінців, необхідно викону вати велику кількість арифметичних дій. По-перше, це робить алгоритм досить громіздким, по-друге, вимагає більше часу на його виконання. Якщо в задачі необхідно дослідити лише два задані відрізки, то, можливо, такий підхід і не є дуже обтяжли вим. Однак у разі, коли дослідження відбувається для значно більшої кількості відрізків, то перевага першого алгоритму не заперечна: у ньому виконуються лише арифметичні дії відні мання та множення і логічні дії порівняння. Відсутність ділен ня значно збільшує ймовірність отримання коректного резуль тату.
Саме в цьому ми матимемо змогу переконатися у наступних алгоритмах, що розглядатимуться.
Визначення положення точки відносно багатокутника
Розглянемо багатокутник на площині, заданий координата ми своїх вершин у порядку їх обходу, та деяку довільну точку (X; Y) (мал. 148). Нас цікавитиме питання, чи належить ця точка заданому багатокутнику.
У |
(х2; |
у2) |
|
У |
|
(*0І Уг) |
|
|
|
|
|
|
|||
|
|
|
х3; у3) |
|
|
|
|
|
to; Уі) (х4; у І) |
|
|
|
fe; yd |
(*?; |
у3) |
|
|
|
|
|
|
||
(0;0^ |
|
|
х |
(0; 0) |
|
|
х |
|
а) |
|
|
|
|
б) |
|
|
|
|
Мал. 148 |
|
|
|
|
Поставлену задачу можна розв'язувати традиційним шля хом: з'єднати точку (X; Y) з кожною із вершин заданого багато кутника, знайти суму площ отриманих трикутників і порівня ти з площею всього багатокутника, алгоритм обчислення зна чення якої вже відомий. Однак, як видно з двох варіантів багатокутників, зображених на малюнку 148, лише для опук лого багатокутника такий алгоритм дасть правильну відповідь (мал. 148, а). У випадку неопуклого багатокутника (мал. 148, б) такий підхід не дасть коректного результату.
260

Підійдемо до розв'язання нашої задачі з дещо іншого боку. Побу дуємо відрізок, який паралельний осі Ох, одним із кінців якого є точка (X; Y), а другим - точка (х'; У), де х' > max(xv х2,..., хп). На ма люнку 124 зображено два варіанти багатокутників та різні розмі щення точки (X; Y) відносно них. Згідно з побудовою відрізків з кінцями (X; Y) і (х'; Y), точка (х'; Y) завжди знаходиться поза межа ми внутрішньої частини багатокутника. А це означає, що для того, аби із точки (X; Y) потрапити у точку (х'; Y), рухаючись цим відріз ком, треба перетинати сторони заданого багатокутника, якщо вони з'являються на цьому шляху. Як видно з малюнків 149, якщо точ ка (X; Y) належить внутрішній частині багатокутника, то таких пе ретинів буде непарна кількість (мал. 149, а, б), якщо ж зовнішній, - то парна (мал. 149, г) або перетини зовсім відсутні (мал. 149, в).
в) |
г) |
Мал. 149
Чи не стане перешкодою випадок, коли побудований відрізок проходитиме через вершини заданого багатокутника? Розглянемо відповідні приклади, зображені на малюнку 150.
На малюнку 150, а точка (X; У) розташована всередині зада ного багатокутника і перетин відрізка з кінцями у точках (X; Y) і (х'; Y) відбувається у вершині (х3; у3). Хоча вершина (х3; у3) на лежить двом сторонам багатокутника, у цьому разі логічно вра хувати лише один перетин. Такий висновок збігається з раніше визначеною ознакою належності заданої точки багатокутнику: кількість перетинів непарна.
Для багатокутника, зображеного на малюнку 150, б, задана точка (X; Y) знаходиться зовні і проходить через його сторони
261
