О.О.П / ооп / 4_кол / К курсовой / Методи побудови алгоритмів та їх аналіз. Караванова Т.П. / 252_337

них може знайтися найближча пара (мал. 167). За описаним алгоритмом пошук пари найближчих точок вівся окремо у лі­ вій та правій частинах, тобто для точок рх, р4, р6 і р2, р3, рь. Із прикладу, зображеного на малюнку 167, можна побачити, що в окремо взятих частинах найменшою є відстань між точками рг і р5. Однак, якщо розглядати всю множину заданих точок, то точки рх ір2 розташовані ще ближче одна від одної. Цієї помил­ ки можна уникнути, якщо додатково на кожному кроці після повернення із рекурсії, маючи поточне значення найменшої відстані між двома точками, дослідити точки, що потрапили у прикордонну зону поточного поділу. При цьому деякі точки, що мають однакове значення по осі абсцис, можуть знаходи­ тись і на самій прямій.

Розглянемо k-w. крок виконання рекурсивного алгоритму. Насамперед необхідно визначити, якої ширини має бути при­ кордонна досліджувана зона. Якщо на поточному кроці значен­ ня найменшої відстані між парою точок становить d, то нас ці­ кавитимуть тільки ті точки, відстань між якими менша.

Прикордонна зона може містити точки як зліва і справа від вертикальної прямої поділу, так і на самій прямій (мал. 168). Оскільки під час поділу множини точок на дві підмножини точ­ ки, що розміщені на самій прямій, можуть потрапити у різні під­ множини, то можливий випадок, коли точка рі буде відноситися до лівої частини, а точка р - до правої. Як видно з малюнка, на поточному кроці визначена пара найближчих точок і знаходить­

292

Звідси можна зробити висновок, що ширина прикордонної області повинна дорівнювати d як справа, так і зліва від лінії поділу (мал. 169). Більшою її робити немає сенсу, оскільки ту­ ди попадуть точки, відстань між якими більша за d, а меншою неможливо, оскільки можна втратити точки, що дадуть кра­ щий результат.

Залишається тільки вирішити питання, яким чином пере­ глядати точки, що потрапили у прикордонну область. Якщо робити це повним переглядом усіх пар точок, то ефективність такого підходу не дуже висока.

Виявляється, цей процес можна звести до лінійного. Чи вар­ то переглядати всі можливі пари точок? Мабуть, ні: ті точки, відстань між якими більша за d, нас не цікавитимуть. А де мо­ жуть знаходитися точки, відстань між якими не більша за d? Вони можуть знаходитися лише у квадраті зі сторонами d, то­ му що відстань між ними і по осі абсцис, і по осі ординат не по­ винна перевищувати d.

Розглянемо лівий квадрат, зображений на малюнку 169, і доведемо, що у ньому може знаходитись не більше 4 точок, які є кандидатами на перегляд. Нехай ці точки знаходяться у вер­ шинах квадрата. У такому випадку умова щодо відстані між ними, яка не перевищує d, виконується. Якщо у середину квад­ рата помістити ще одну п'яту точку, то, де б вона не знаходила­ ся, серед решти чотирьох точок знайдеться хоча б одна, від­ стань до якої d' і має місце умова d' < d. А це означає, що саме відстань d' є найменшою і в такому разі ширина лівої частини прикордонної області визначена невірно.

Отже, можна підсумувати, що у лівій частині прикордонної області на кожному кроці слід досліджувати відстань лише між чотирма точками, які розміщені у масиві уі підряд (і = і', і' + 1, V + 2, і' + 3). Звичайно, що ці чотири точки не обов'язково по­ винні бути розташовані у вершинах квадрата зі стороною d, як це зображено на малюнку 169, вони можуть бути і всередині цього квадрата.

Аналогічно доведення проводиться і для квадрата, що зна­ ходиться у правій частині прикордонної області. Таким чином, загальна кількість досліджуваних точок, які розміщені у ма­ сиві уі підряд, становить 8 (на малюнку 169 точки, що наклада­ ються із лівої та правої частин, зображено незафарбованими). А це означає, що після визначення на й-му кроці найменшої відстані d між парами точок у лівій та правій підмножинах необхідно для кожної точки прикордонної області знайти найменшу відстань до кожної із семи наступних у масиві уг Якщо така відстань виявиться меншою за d, то вона є результа­ том пошуку на /г-му кроці.

293

Опишемо алгоритм визначення пари найближчих точок.

1 Упорядкувати за зростанням масив xt та масив уі множи­ ни заданих точок.

2. Прийняти L = 1, R = п.

3. Обчислити m-(L + В) div 2.

4. Розбити елементи масиву xt на дві частини xL (L = 1, 2,..., т),

xR (R = т + 1, т + 2, ..., п).

5. Розглянути ліву під множину точок, що відповідають ма­

сиву xL.

6. Якщо кількість елементів у масиві більша за 3, то пере­ йти до п. 3.

7.Визначити найменшу відстань d між трьома точками мно­ жини.

8.Якщо підмножина точок, що розглядається, є правою, то визначити точки, які входять до прикордонної області, і знай­ ти для них найменшу відстань. Для цього розглядати групи по

вісім точок, що упорядковані за зростанням у масиві уг Якщо обчислена відстань є меншою за d, то прийняти її як d.

9.Розглянути праву під множину точок, що відповідають

масиву xR.

10.Якщо кількість елементів у масиві більша за 3, то пере­ йти до п. 3.

11.Визначити найменшу відстань d між трьома точками множини.

12.Якщо підмножина точок, що розглядається, є правою, то визначити точки, які входять до прикордонної області, і знайти для них найменшу відстань. Для цього розглядати групи по вісім точок, що упорядковані за зростанням у маси­ ві у.. Якщо обчислена відстань є меншою за d, то прийняти її як d.

Для реалізації алгоритму мовою програмування необхідно ввести деякі домовленості. Після упорядкування масивів xt та у. у п. 1 буде порушено відповідність між координатами зада­ них точок. Для збереження цієї інформації можна використати масив pt, у якому міститимуться порядкові номери елементів масиву yt, що відповідають точкам із масиву хг Наведемо при­ клад. Нехай задано три точки з координатами;?^; 5),р2(1; 10), р3 (4; 12). Спочатку упорядкуємо масив xt за зростанням з одно­ часним перенесенням відповідних елементів масиву yt: xt(l; 2; 4), yt(10; 5; 12). Якщо тепер виконати упорядкування за зростан­ ням у масиві yt, то відповідність координат заданих точок буде порушена: yt= (5; 10; 12). Але якщо у масиві/?, сформувати та­ ку інформацію (2; 1; 3), то це означатиме, що ордината точки з абсцисою хх = 1 міститься у масиві уі під порядковим номером pv а саме на 2-му місці.

294

З урахуванням усього зазначеного вище фрагмент основної програми, що реалізує алгоритм визначення пари найближчих точок, запропонований Шамотом, виглядатиме так:

у1 := а; {Збереження відсортованої по осі ординат вхідної інформації у масиві у.) dist( 1, п); {Визначення найменшої відстані між заданими точками.}

Варто розглянути ще процедуру, яка упорядковує послідов­ ність координат заданих точок як по осі абсцис, так і по осі ор­ динат:

if j > Lthensort(L, j); if i< Rthensort(i, R)

end;

Рекурсивна процедура dist, яка визначає мінімальну від­ стань між парою точок:

procedure dist(L, R: word); var і, j, m, k: word;

begin

І := L; j := R; m := (L + R) div 2; {Розбиття поточної групи точок на дві підгрупи.} if j - І <= 2 {Якщо кількість точок у групі менше трьох,}

295

/

begin

d := sqrt(sqr(x[i] - x[k]) + sqr(y[i] - y[k])); {обчислення відстані і,}

Процедура limit, яка визначає мінімальну відстань між па­ рою точок у прикордонній області:

if p[k] < min then min := p[k];

if p[k] >= max then max := p[k]; end;

inc(k)

end;

296

k := min; flag := false; * '

r e p e at {Перегляд групи із 7-ми точок, розташованих послідовно на осі ординат.}

until ((L <= p[k]) and (p[k] <= R)) or flag; until flag;

end;

Оцінка ефективності алгоритму, що визначає пару найближ­ чих точок, складається із двох частин. На першому етапі вико­ нання алгоритму упорядкування за зростанням масиву х1 ста­ новить 0(п logn). Подальші етапи базуються на роботі із упо­ рядкованими фрагментами масивів хі та yt, тому вони є ліній­ ними і їх оцінка становить 0(п). Тому у підсумку загальна оцінка описаного алгоритму визначається як 0(п logn).

Під час тестування алгоритму визначення пари найближ­ чих точок необхідно врахувати як кількість заданих точок п ^ 10, п < 100, п ^ 1000, так і їх розміщення. А саме варто роз­ глянути випадки, коли точки рівномірно розподілені по пло­ щині, коли більша їх частина потрапляє у прикордонну об­ ласть, коли досить велика кількість точок мають однакове зна­ чення по осі абсцис, тобто розміщені на вертикальній прямій, і одночасно потрапляють на вертикальну пряму поділу.

Найвіддапеніші точки

Найвіддаленіші точки серед множини заданих можна у наоч­ ний спосіб знайти таким чином. Спочатку визначити послі-

297

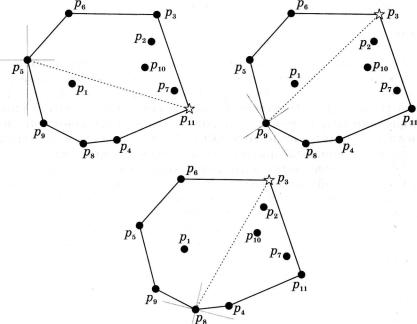
довність вершин опуклої оболонки, оскільки тільки серед цих точок може існувати шукана пара. Потім візуально уявити собі побудовану опуклу оболонку затиснутою між двома рухливими вертикальними прямими на площині. Під час її провертання, наприклад, за годинниковою стрілкою, відстань між верти­ кальними прямими буде змінюватися. Те значення відстані, що виявиться найбільшим, і координати точок, що лежатимуть на вертикальних прямих, дадуть шуканий результат.

Яким же чином алгоритмічно реалізувати запропоновану ме­ тодику пошуку пари найвіддаленіших точок серед множини за­ даних? Зрозуміло, що пошук таких пар необхідно здійснювати покроково для кожної вершини опуклої оболонки. Можна запро­ понувати ідею паралельного перенесення початку координат послідовно у кожну вершину і повороту системи координат таким чином, щоб усі точки знаходились у правій координатній півплощині. Тоді розв'язок на поточному кроці зведеться до пошуку вершини, що має найбільше значення по осі абсцис (мал. 170). Серед усіх таких значень необхідно знайти найбільше, і це зна­ чення буде відповіддю на поставлене питання.

Питання перетворення координат на площині розглядати­ муться далі, тому питання реалізації запропонованого алгорит­ му у даній темі не розглядатиметься.

Мал. 170

298

І

Простішим є алгоритм, у якому для кожної з k вершин опук­ лої оболонки визначаються відстані до решти вершин. Такий алгоритм можна вважати повноперебірним.

Порівняльна оцінка обох запропонованих алгоритмів визна­ чення пари найвіддаленіших точок серед множини заданих ви­ глядатиме так. В обох випадках оцінимо пошук опуклої оболон­ ки як 0(п logn). Для першого алгоритму, що базується на пере­ творенні координат на площині, буде виконано k кроків. На кожному із цих кроків обчислюються нові значення координат k вершин опуклої оболонки по осі абсцис і одночасно шукається найбільше серед них, тобто 0(k). Загальна оцінка цього алгорит­ му становитиме 0(п logn + k) = 0(п logn). Для другого алгоритму повний перебір вершин опуклої оболонки вимагає k2 кроків. То­ му загальна його оцінка обчислюється як 0(п logn + k2). Якщо більша частина заданих точок є вершинами опуклої оболонки, то зрозуміло, що алгоритм, який базується на перетворенні ко­ ординат точок на площині, має значні переваги.

Для тестування обох алгоритмів бажано розглянути різні ви­ падки розташування точок на площині: кількість вершин опук­ лої оболонки значно менша за кількість заданих точок, більшість заданих точок є вершинами опуклої оболонки, усі задані точки є вершинами опуклої оболонки. Усі ці випадки слід розглянути для різної кількості заданих точок: п % 10, п К 100, п < 1000.

Завдання

1.Розробити та реалізувати у вигляді програми алгоритм ви­ значення пари найближчих точок.

2.Розробити та реалізувати у вигляді програми алгоритм ви­ значення пари найвіддаленіших точок.

3.Виконати завдання 1-2 для кількості точок N ^ 10, які рів­ номірно розподілені по площині. Результат виконання прог­ рами вивести у файл.

4.Виконати завдання 1-2 для кількості точок N =С 10, більшість з яких потрапляє у прикордонну область при першому поділі їх на дві частини. Результат виконання програми вивести у файл.

5.Виконати завдання 1-2 для кількості точок N € 10, біль­ шість з яких розміщена на вертикальній прямій, що ділить їх на дві частини на першому кроці виконання алгоритму. Результат виконання програми вивести у файл.

6.Виконати завдання 1-2 для кількості точок N К 10, згенерованих випадковим чином. Результат виконання програми вивести у файл.

7.Виконати завдання 3-6 для кількості вершин ./V ^ 100. Ре­ зультат виконання програми вивести у файл.

8.Виконати завдання 3-6 для кількості вершин N ^ 1000. Ре­ зультат виконання програми вивести у файл.

9.Зробити письмовий аналіз завдань 3-8.

299

/ Запитання для самоконтролю

1. У чому полягає суть задачі визначення пари найближчих точок? Яка її практична цінність?

2. Який алгоритм визначення пари найближчих точок дає оцінку ефективності виконання 0(л2)? У чому він полягає?

3. Ким запропонований алгоритм визначення пари найближчих то­ чок і на якому методі він базується? Проілюструйте застосуван­ ня цього методу на власному прикладі.

4. Як визначається найменша відстань між парою точок в одній із підмножин?

5. З чим пов'язана необхідність розгляду точок у прикордонній об­ ласті?

6. Як визначається пара найближчих точок у прикордонній області? 7. Як довести той факт, що для визначення пари найближчих точок у прикордонній області достатньо розглядати лише певну групу

точок?

8. Яким є алгоритм визначення пари найближчих точок?

9. Опишіть алгоритм визначення пари найближчих точок.

10. Наведіть фрагмент програми, що реалізує алгоритм визначення пари найближчих точок. Поясніть необхідність використання ма­ сиву рп застосування значень його елементів та їх формування.

11. Обґрунтуйте виведення оцінки ефективності роботи алгоритму визначення пари найближчих точок.

12. Як можна знайти пару найвіддаленіших точок? Серед яких точок множини слід шукати пару найвіддаленіших точок?

13. Наведіть власний приклад множини точок і продемонструйте покрокове виконання алгоритму визначення пари найвіддаленіших точок.

14. Який простіший алгоритм дає змогу визначити пари найвідда­ леніших точок?

15. Якими є оцінки ефективності виконання обох алгоритмів визна­ чення пари найвіддаленіших точок? Обґрунтуйте свою відповідь.

Перетворення координат точок на площині

Як відомо, екранні координати точок відмінні від координат на площині у декартовій системі. Основні відмінності у тому, що екрані координати точок визначаються тільки цілими та додатними значеннями, і, на відміну від декартової системи, відлік значень по осі абсцис та по осі ординат починається з лі­ вого верхнього кута екрана. Окрім цього для розробки анімаційних алгоритмів важливим є також і знання алгоритмів пе­ ретворення координат точок під час їх переміщення як на пло­ щині, так і у просторі.

Розглянемо точку М, що визначається на площині коорди­ натами (X; Y) (мал. 171). При переміщенні точки М на площині відносно заданої декартової системи змінюватимуться значен­ ня її координат. До цього процесу можна підійти з двох боків: або змінити систему координат, переносячи її початок і оберта­ ючи на площині, або вважати, що сама точка перемістилася на

300

інше місце у тій самій системі координат. Далі буде розгляда­ тися саме другий підхід. Тому вважатимемо, що заданій точці М з координатами {х; у) у тій же системі координат ставиться у відповідність точка М* з координатами (х*; у*).

Усі перетворення, які необхідно зробити для переведення точки М у точку М*, можна представити такими кроками.

1. Поворот навколо початку координат (мал. 171, а) на кут ф описується формулами:

х* = х coscp - у sincp; у* = х sincp + у coscp.

2. Розтягування або стиснення для переміщення точки по­ чатку координат уздовж координатних осей (мал. 171, б) мож­ на задати так:

х = ах; у = оу.

Наприклад, розтягування (стиснення) вздовж осі абсцис за­ безпечується за умови, що а < 1 (а > 1).

3. Відображення (відповідно осі абсцис) у разі, коли система координат змінює напрям (мал. 171, в), задається формулами:

х* = х;у* = -у.

Для більш компактного представлення послідовності описа­ них перетворень координат заданої точки М для її переміщен­ ня в іншу систему координат, що аналогічне переведенню її у точку М*, можна запропонувати такий запис:

Перетворення координат точок у просторі

Перетворення координат точок у просторі аналогічні до тих, що виконуються для перетворень на площині, однак повинні враховувати те, що повороти повинні виконуватися навколо всіх осей координат.

301