О.О.П / ооп / 4_кол / К курсовой / Методи побудови алгоритмів та їх аналіз / 62_201

Якщо ця сумарна відстань через вершину виявиться меншою, то надалі необхідно враховувати саме її. Отже, ми отримали ту са­

му формулу, що і в алгоритмі Дейкстри: dtj = min{dtj, dik + dkj). А тепер запишемо сам алгоритм:

1. Визначити вершину графа k = 1, через яку буде здійсню­ ватися перерахунок відстані між вершинами і та j.

2. Визначити вершину і = 1.

3. Визначити вершину; = 1.

4. Якщо величина dik + dkj менша за значення dtj, то замінити значення dt. на di k + dk •. В іншому разі залишити зна­ чення d. без змін.

5. Якщо j ^ п, то перейти до наступної вершини у + 1 і повер­ нутися до п. 4.

6. Якщо і ^ п, то перейти до наступної вершини і + 1 і повер­ нутися до п. 3.

7. Якщо k <ї п, то перейти до наступної вершини k + 1 і повер­ нутися до п. 2.

8. Завершити алгоритм.

У результаті виконання алгоритму елементи dt • будуть міс­ тити наикоротшу відстань між відповідними вершинами графа

і та j .

Реалізація алгоритму Флойда-Уоршелла мовою Pascal буде такою:

for k := 1 to n do for і := 1 to n do forj := 1 to n do

ifd[i, k] + d[k, j] < d[i, j] thend[i,j]:=d[i, k] + d[k,j];

Як бачимо, алгоритм найпростіший як у розумінні, так і в його реалізації. Єдине, що слід обов'язково зазначити, це те, що за даним алгоритмом не можна визначити шлях між вершина­ ми і та j, який дає визначений найкращий результат. Тому, як­ що умова задачі вимагає цієї інформації, то слід все-таки засто­ сувати алгоритм Дейкстри для кожної вершини заданого графа.

Завершимо ознайомлення з алгоритмом Флойда-Уоршелла однією практичною порадою. Під час реалізації алгоритму у вигляді програми слід підібрати таке значення елементів d[i, j], що відповідає поняттю «безмежність», тобто відсутність ребра між вершинами і та /і

Нагадаємо оцінку алгоритму Флойда-Уоршелла, яка була дана на початку. Вона становить 0(п3) і визначається за кіль­ кістю вкладених циклів, що реалізують описаний алгоритм.

Для тестування алгоритму Флойда-Уоршелла можна ви­ користати ті самі тести, що й для алгоритму Дейкстри. Це дасть змогу перевірити коректність роботи обох алгоритмів.

112

Завдання

1.Розробити та реалізувати у вигляді програми алгоритм Дейкстри для заданого графа.

2.Виконати завдання 1 для зваженого неорієнтованого графа з кількістю вершин N < 10. Результат виконання програми вивести у файл.

3.Виконати завдання 1 для зваженого орієнтованого графа з кількістю вершин N ^ 10. Результат виконання програми вивести у файл.

4.Виконати завдання 2-3 для графа з кількістю вершин N = 100. Результат виконання програми вивести у файл.

5.Розробити та реалізувати у вигляді програми алгоритм Флойда-Уоршелла для заданого графа.

6.Виконати завдання 5 для зваженого неорієнтованого графа з кількістю вершин N ^ 10. Результат виконання програми вивести у файл.

7.Виконати завдання 5 для зваженого орієнтованого графа з кількістю вершин N ^ 10. Результат виконання програми вивести у файл.

8.Виконати завдання 6-7 для графа з кількістю вершин N = 100. Результат виконання програми вивести у файл.

1.У чому полягає задача визначення найкоротшого шляху між дво­ ма вершинами заданого графа?

2.Для яких графів можна застосувати алгоритм Дейкстри?

3.У чому полягає основна ідея алгоритму Дейкстри?

4.Сформулюйте і запишіть алгоритм Дейкстри.

5.На власному прикладі продемонструйте покрокове виконання алгоритму Дейкстри.

6.Запишіть варіант реалізації алгоритму Дейкстри мовою Pascal.

7.Які описи змінних необхідно зробити для виконання програми, що реалізує алгоритм Дейкстри?

8.Яким чином можна вивести шлях, який дає найкоротшу відстань між двома заданими вершинами у графі?

9.Якою є оцінка виконання алгоритму Дейкстри? Обґрунтуйте свою відповідь.

10.Яку задачу призначений розв'язувати алгоритм Флойда-Уор­ шелла?

11.Якою є оцінка виконання алгоритму Флойда-Уоршелла? Обґрунтуйте свою відповідь.

12.Сформулюйте і запишіть алгоритм Флойда-Уоршелла.

13.Яким чином реалізується алгоритм Флойда-Уоршелла мовою Pascal? Запишіть фрагмент програми.

14.Яким чином реалізувати задачу визначення найкоротшого шля­ ху між усіма парами вершин заданого графа і відповідних їм шляхів?

113

Точки з'єднання та мости в графі

Досі ми розглядали алгоритми на графах, що не міняли їх будови: шукали задані вершини в графі, тобто визначали їх до­ сяжність, будували остовні дерева, шукали найкоротший шлях між парами вершин тощо. Але жодна з розглянутих задач не «пошкоджувала» початковий стан заданого графа. Однак на практиці існують задачі, коли необхідно за певних сформульованих умов визначити, які вершини або ребра слід прибрати для досягнення поставленої мети.

Наприклад, яку мінімальну кількість вершин або ребер у за­ даному графі необхідно вилучити, щоб заданий зв'язний граф розпався на максимальну кількість окремих зв'язних графів, тобто під графів? Так може трактуватися задача про боротьбу з монополізацією деякої галузі виробництва, стратегічним пе­ рекриттям доріг для максимального поділу міста-велетня на окремі міні-райони тощо.

Отже, почнемо розгляд таких задач із введення нових термінів.

Не завжди існують лише зв'язні графи. Наприклад, графом є як структура доріг одного населеного пункту, так і система, що складається з окремих населених пунктів. За відсутності трас, що ведуть до кожного з таких населених пунктів, можна вважати цей граф незв'язним. Отже, кількість зв'язних під-

графів, з яких складається заданий граф, називається компо­ нентою зв'язності заданого графа. На малюнку 63 зображено різні графи, для яких визначено компоненти зв'язності.

Точкою з'єднання (або поділу) у графі називається така вер­

шина, вилучення якої збільшує кількість компонент зв'язності заданого графа. Зрозуміло, що в разі вилучення деякої верши­ ни графа вилучаються і всі ребра, яким вона належить, оскіль­ ки в графі не може бути ребра, один з кінців якого не належить

114

множині вершин. Наприклад, на малюнку 63, а такою верши­ ною є вершина 7. У разі її вилучення заданий граф, що має кількість компонент зв'язності 0, розпадається на два окремих зв'язних підграфи: (6,1), (1,2) та (5,4), (4,3). Тобто кількість компонент зв'язності в заданому графі збільшується на 2.

Граф, який містить хоч одну точку з'єднання, називається

подільним.

Граф, який не містить жодної точки з'єднання, називається

двозв'язним, або неподільним.

Двозв'язний підграф заданого графа називається компо­ нентою двозв'язності.

Двозв'язність графа - дуже бажана ознака графа під час розв'язування деяких задач. Наприклад, вершини графа відповідають вузлам деякої інформаційної мережі, а ребра - лініям передачі. Якщо наш граф двозв'язний, то вихід з ладу будь-якого окремого вузла ніколи не призведе до втрати зв'язку між будь-якими двома вузлами, що не збігаються з пошкодже­ ним. І ще один приклад. Мережа водопостачання в населеному пункті є не що інше, як зв'язний граф. Подекуди виникає не­ обхідність у технічному відключенні деяких вузлів цієї мережі. Знання точок з'єднання такого графа дасть змогу ефективніше виконати роботи, не залишивши все населення без води.

Точку з'єднання в заданому графі можна визначити вже відомими нам алгоритмами. Найпростіший варіант - це засто­ сування алгоритму пошуку в глибину з покроковим виключен­ ням усіх вершин заданого зв'язного графа з метою перевірки зв'язності графа. Якщо після виключення деякої вершини графа він стає незв'язним, то можна стверджувати, що дана вершина є точкою з'єднання. Однак слід погодитися, що такий алгоритм не є найкращим, оскільки виконується стільки разів, скільки є вершин у заданому графі.

Чи можна запропонувати ефективніший алгоритм? Вияв­ ляється, так, і зараз ми його розглянемо. Але спочатку сформу­ люємо кілька незаперечних фактів. Для цього розглянемо малю­ нок 64. На ньому зображено граф, який утворюється з трьох двозв'язних підграфів А, В, С за допомогою точок з'єднання а та Ь.

Отже, якими фактами можна оперувати?

1. Для того щоб обійти всі вершини заданого графа, не­ обхідно, використовуючи алгоритм пошуку в глибину, перехо­ дити від однієї вершини до іншої, записуючи нові зустрінуті вершини у стек. Зайшовши в тупик, необхідно у стеку поверну­ тися на одну вершину назад і спробувати вийти на нову, ще не переглянуту вершину. Лише після повернення до початку сте­ ку і «зібравши» у множині всі вершини графа, можемо конста-

115

Мал. 64

тувати, що повністю обійшли граф, і стверджувати факт зв'яз­ ності заданого графа.

2.Нехай ми починаємо рух заданим графом (мал. 64) з будьякої вершини, що належить компоненті двозв'язності А. Оскільки граф зв'язний, то ми зможемо обійти всі вершини. Але попасти з підграфа А у підграф В і повернутися назад змо­ жемо лише пройшовши двічі через вершину а. Те саме сто­ сується і підграфа С: обхід його вершин і повернення назад у підграф А можливе лише за умови подвійного відвідування вершини Ь під час входу у підграф і під час виходу з нього.

3.Яку цікаву інформацію можна при цьому отримати і як нею скористатися? Якщо всі вершини графа нумерувати в по­ рядку черговості їх першого відвідування в процесі обходу гра­ фа, то очевидно, що всі вершини підграфа В будуть мати номе­ ри, більші за значенням, ніж номер вершини а, а підграфа А - менші. Аналогічний висновок можна зробити відносно верши­ ни Ь та під графів А і С: порядковий номер вершини Ь буде біль­ ший, ніж у всіх вершин підграфа А, і менший, ніж у всіх вер­ шин підграфа С.

4.Надалі будемо розрізняти існуючі між вершинами і та / ребра (і, j) і (j, і). Насправді це одне й те саме ребро, але в пер­ шому варіанті ми дивимося з вершини і у вершину /, а в друго­ му - навпаки. Нехай перше ребро - це те, яким ми проходимо від раніше вже відвіданої вершини і у нову знайдену вершину /. При цьому порядковий номер вершини j буде більшим за номер вершини і. Друге ребро (у, і) зустрінемо тоді, коли побачимо з вершини j, що має більший порядковий номер, вершину і з меншим порядковим номером.

5.Оскільки В - компонента двозв'язності, то кожна верши­ на цього підграфа буде бачити лише вершину цього самого підграфа, порядковий номер якої більший за номер вершини а.

116

Це означає, що ми увійшли в підграф В через вершину а і тіль­ ки через неї можемо вийти. Для прикладу на малюнку 64 пунк­ тиром зображено ребро, що з'єднує деяку вершину / підграфа В з деякою вершиною і підграфа А. Коли ми будемо знаходитись у підграфі В і з вершини у побачимо вершину і, що має менший порядковий номер, ніж вершина а, через яку ми дісталися у В, то це означатиме, що у підграф В можна зайти не лише через вершину а, а тому вона не є точкою з'єднання.

6. І ще одним з важливих моментів, який може виникнути під час пошуку точки з'єднання, є поняття «тупика». Тупико­ ва ситуація під час обходу графа у глибину може скластися у двох випадках: перший - ми переглянули всі вершини компо­ ненти двозв'язності і повернулися у вершину, яка є точкою з'єднання, а другий, коли ми знаходимося в середині компо­ ненти двозв'язності і переглянули всі її вершини.

Отже, головною ознакою того, що вершина а є точкою з'єднання, є така обставина: всі вершини компоненти двозв'яз­ ності заданого графа мають порядкові номери більші, ніж відповідна їй точка з'єднання, і бачать вершини, порядкові но­ мери яких менші за порядкові номери самих цих вершин, але не менші, ніж порядковий номер точки з'єднання.

Таким чином, для реалізації алгоритму визначення точок з'єднання заданого графа необхідно для кожної вершини зберігати подвійну інформацію: порядковий номер цієї верши­ ни, отриманий у процесі обходу графа пошуком у глибину, і мінімальний порядковий номер вершини, яку можна з неї по­ бачити в процесі такого обходу.

Ознакою того, що наша вершина а під час повторного її пе­ регляду, тобто після повного обходу вершин у компоненті двозв'язності В і повернення в а, є точкою з'єднання, буде те, що попередня вершина, зображена в підграфі В на малюнку 64, з якої ми повернулися в а, могла бачити лише вершину з біль­ шим порядковим номером, ніж вершина, зображена на малюн­ ку 64 в підграфі А, і яка передувала вершині а під час обходу графа.

Перейдемо до опису алгоритму визначення точок з'єднання у зв'язному графі. Для зручності введемо такі позначення: order\ - порядковий номер вершини і, який вона отримає в про­ цесі обходу графа, indi - індекс вершини і, що є найменшим по­ рядковим номером іншої вершини, яку можна побачити з вер­ шини і.

1.Визначити вершину графа start, з якої буде вестися пере­ гляд вершин заданого графа, занести її у стек (top := 1), а поряд­ ковий її номер у масиви order та ind.

2.Якщо стек вичерпано (top = 0) і пройдено всі вершини гра­ фа, то перейти до п. 12.

117

3.Визначити вершину і, яка записана у вершині стеку, як поточну.

4.Визначити вершину j, для якої існує ребро (і, j).

5.Якщо не існує ребра (і, j), тобто ми потрапили в тупик, то перейти до п. 8.

6.Якщо вершина / є новою, то записати її у вершину стеку, зробити поточною (і := j) і перейти до п. 3.

7.Якщо вершина j вже була занесена в стек, тобто не є но­ вою, її порядковий номер у стеку менший, ніж у вершини і, з якої ми на неї дивимося (order[j] < order[i]), і менший, ніж но­ мери вершин, які ми бачили з вершини і (order[j] < ind[i]), то необхідно перерахувати індекс вершини і, як тієї, що побачила відвідану вершину з номером, меншим, ніж усі досі видимі з неї (ind[i] := order\J]). Перейти до п. 4.

8.Якщо в стеку залишився один елемент (top = 1), то пере­ йти до п. 12.

9.Перш ніж зменшити значення вершини стеку на 1 (top := top - 1), необхідно розглянути останні дві вершини і тау, записані в ньому, і ребро (i,j), що їм відповідає.

10.Якщо з вершини j було «видно» лише вершини, що ма­ ють порядкові номери більші, ніж вершина і, тобто всі вони бу­ ли пройдені під час обходу графа після неї (order\i\ <= ind[j]), то вершина і є точкою з'єднання. Перейти до п. 3.

11.Якщо з вершини j було «видно» вершини з меншими по­ рядковими номерами, ніж з вершини і (ind[j] < ind[i]), і між ни­ ми існує ребро (i,j), то це означає, що з вершини і можна діста­ тися цих вершин також. Тому необхідно перевизначити індекс вершини і (ind[i] := ind[j]) і перейти до п. 3.

12.Завершити алгоритм.

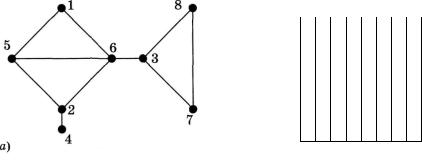
Традиційно розглянемо конкретний приклад і виконаємо описаний алгоритм покроково (мал. 65).

Зображатимемо сам граф, номери його вершин (верхній ря­ док у таблиці), стан стеку (stack - зліва від таблиці), масив по­ рядкових номерів вершин у процесі обходу графа (order - дру-

б)

Мал. 65

118

гий рядок у таблиці) та масив індексів цих вершин (ind - третій рядок у таблиці). Початковий стан елементів масиву порядко­ вих номерів є значення 0, а їхніх індексів - 9. Це дасть змогу за допомогою значень порядкових номерів вершин визначати, чи побачена вершина є новою, чи вже зустрічалася нам раніше. А для індексів значення 9 надасть можливість для подальшого покращання цього значення, оскільки вершин з таким поряд­ ковим номером у нашому графі точно не трапиться.

Нехай стартовою вершиною буде вершина 5. На першому кроці у стек буде занесено вершину 5, а її поточним номером буде відповідно 1 (мал. 66, а). З вершини 5 першою ми побачи­ мо вершину 1 (п'ятий рядок таблиці суміжності мал. 65, б). Це нова вершина, оскільки її порядковий номер дорівнює 1, тому допишемо її у стек, а її порядковий номер обходу 2 - у масив порядкових номерів (мал. 66, б).

З вершини 1, згідно з першим рядком таблиці суміжності, ми знову побачимо вершину 5. Оскільки вона не нова і її поряд­ ковий номер менший за порядковий номер вершини 1, то змі­ нимо індекс останньої. Він тепер дорівнюватиме 1 (мал. 67, а). Це означає, що з вершини 1 ми змогли побачити вершину 5, порядковий номер якої 1 менший, ніж у вершини 1 (2). Наступ­ ною вершиною (1-й рядок таблиці суміжності), яку видно з вер­ шини 1, є вершина 6. Вона нова, оскільки в масиві порядкових номерів order6 = 0. Записуємо її у стек і в масиві порядкових номерів надаємо order6 значення 3 (мал. 67, б).

Переходимо до розгляду вершини 6, а саме у 6-й рядок таб­ лиці суміжності. Значення 1 зустрічається для першого еле­ мента цього рядка. З малюнка 65 бачимо, що справді з верши­ ни 6 видно вершину 1, в якій вже побували, і тому маємо змогу

119

б) Мал. 67

перевизначити значення індексу вершини 6. Вершина 1 має по­ рядковий номер 2, який менший, ніж порядковий номер поточ­ ної вершини 6 (3), і менший, ніж значення її індексу (9). Тому визначимо індекс вершини 6 значенням 2, і це означатиме, що з вершини 6 ми зможемо бачити вершину з меншим порядко­ вим номером (2), тобто вершину 1 (мал. 68, а).

Продовжуємо перегляд 6-го рядка таблиці суміжності. На­ ступна «видима» вершина з номером 2. Вона нова, і тому запи­ суємо її у стек, а її порядковий номер - у 2-й елемент масиву order (мал. 68, б).

Переходимо до 2-го рядка таблиці суміжності і визначаємо першу в цьому рядку видиму вершину. Нею є нова вершина 4.

120

(мал. 69, а). З вершини 4 можна побачити вершину 2, і тому спочатку необхідно перевизначити її індекс. Вершина 2 з по­ рядковим номером 4 була побачена раніше, ніж вершина 4 з по­ рядковим номером 5, а це означає, що індексом вершини 4 тепер буде значення 4 (мал. 69, б).

Вершина 4 є тупиковою, оскільки жодної нової вершин з неї ми не можемо побачити. Згідно з описаним алгоритмом, ми повинні повернутися до попередньої вершини, яка записана в стеку, тобто до вершини 2, і розглянути ребро (2,4). У разі потрапляння в тупик необхідно визначити, чи порядковий но­ мер вершини 2 не перевищує індекс вершини 4. У нашому ви­ падку цей факт справджується: order2 ^ ind4, (4 = 4), тому вер­ шина 2 є точкою з'єднання (мал. 70, а).

121