Сортування методом Шелла

Цей метод був запропонований Дональдом Л. Шеллом у 1959 р. Цей метод (ShellSort) дає змогу здійснювати сортування за допомогою включения з відстанями, що зменшуються, і ба-зується він на іде'і методу прямого включения.

Розглянемо відомий уже нам масив:

44, 55, 12, 42, 94, 18, 06, 67.

Спочатку впорядкуємо елементи, які знаходяться на відста-ні 4 один від одного (мал. 55).

41

55

12

42 94

Мал. 55

18

0G

G7

3 малюнка видно, що методом включения впорядковуються такі групи: 44 і 94, 55 і 18, 12 і 06, 42 і 67. У результаті вико-нання впорядкування в кожній групі отримаємо такі групи: 44 і 94, 18 і 55, 06 і 12, 42 і 67. Оскільки впорядкування відбу-валося на сво'їх місцях, то результатом його буде масив:

44, 18, 06, 42, 94, 55, 12, 67.

Тепер розглянемо групи елементів, що знаходяться на від-стані 2 один від одного. Такий крок обрано для того, щоб «за-хопити» результат попереднього обміну (мал. 56).

Мал. 56

Випишемо і в цьому разі ті групи елементів, які сортуються методом включения: перша - 44,06,94,12, друга -18,42,55,67. Застосувавши метод включения до кожної з них, отримаемо: першу - 06, 12, 44, 94; другу - 18, 42, 55, 67. У результаті маемо такий масив:

06,18,12,42,44,55,94,67.

Залишилося зробити останне впорядкування методом вклю­чения, утворюючи групи з кроком 1 (мал. 57).

162

06 18 12 42 44 55 94 67

Мал. 57

Тепер у результата застосування методу включения отри-маемо остаточний вигляд відсортованого масиву:

06,12,18, 42, 44, 55, 67, 94.

Зрозуміло, що у випадку поділу масиву на групи з кро-ком 1 ми насправді розглядаємо повністю сам масив, тобто від-бувається звичайне сортування. Але на ней момент масив уже майже відсортовано, тому, застосовуючи метод включения, зводимо до мінімуму кількість переставлень елементів масиву. Те саме можна сказати і про всі попередні кроки.

Тепер необхідно визначитися, яким чином найоптимальні-ше визначати кроки для поділу заданого масиву на групи. У ре­зультат! своїх досліджень Д. Кнут показав, що мае сенс вико-ристовувати такі послідовності кроків:

1) 1, 4, 13, 40, 121, ..., де h_h = ЗЛ, + 1;

2)l,8,7,15»31,...,flBft_t-2V_l+l.

Яким чином вибрати ту чи іншу залежність для кроків при

сортуванні методом Шелла? Можливо, це залежить від довжи-ни масиву: для невеличких масивів — перший варіант, для ве­ликих — другий. Хоча поняття «малий» і «великий» дуже від-носне.

Час уже навести текст програми мовою Pascal, що реалізує описаний алгоритм. Спочатку нагадаємо алгоритм, що відпові-дає методу прямого включения, і оформимо його у вигляді про-цедури:

procedure InsertionSort; varx, j: word; begin

x:=a[i];j:=i; while x < a[j - h] do begin

a[j]:=a[j-h]; j:=j-h end; a[j] := x end;

Проаналізувавши текст наведеної процедури, можна зроби-ти висновок, що вона дає змогу включити елемент а_і у трупу елементів, які передують йому в заданому масиві, а значения індексів сусідніх елементів відрізняється на h. Тепер основна

в*

163

частина алгоритму, що реалізує метод Шелла, виглядатиме так:

while h > = 1 do {Повторения алгоритму з наступним кроком л.}

begin

j:=1;i:=1;

while j <= n - h do {Визначення початкового елемента}

begin {кожної фупи з кроком л.}

і := і + h;

while і <= n do {Включения кожного елемента a[i]}

begin {у попередню частину визначеної групп з кроком л.}

InsertionSort; inc(i, h) end; inc(j);i:=j; end;

{Перерахунок кроку л за визначеним алгоритмом} h := (h - 1) div 3; {або h •= (h - 1) div 2.)

end;

Для того щоб визначити початкове значения величини Л, яке містить значения максимального кроку поділу заданого масиву на групи, можна запропонувати такий алгоритм: бу-демо збільшувати значения h за формулою h_k = 3A_k_, + 1 або h_h ■ 2/»j_j + 1 доти, доки воно не перевершить кількості елемен-тів масиву п:

h_new := 1; while h_new <= n do begin

h_old := h_new; h_new := 3 * h_old + 1; end; h:=h_old;

Однак тестування наведеного варіанта алгоритму, що реалі-зує метод Шелла, показали не дуже втішні результати. Для ве­ликих п вони виявилися значно гіршими, ніж у наступних удосконалених методах, які розглянемо далі.

У своїй праці Н. Вірт розглядає питания методів сортування та пропонуе алгоритм сортування масиву методом Шелла з ви-користанням так званих бар'єрів. Це аналогія використання змінної а₀ в алгоритмі прямого сортування методом включен­ия, який відіграє роль бар'ера при включенні елемента а. у під-послідовність Oj ... a_t__v Оскільки сортування методом вклю­чения з відстанями, що зменшуються, використовує під час сортування різні підпослідовності з кроком h, то й необхідно для кожної такої групи використовувати відповідно свій бар'єрний елемент. Для цього резервуються елементи у масиві

164

а[ - h_max..n]. Наведемо текст Pascal-процедури, що безпосе-редньо реалізує цей варіант алгоритму включения:

procedure InsertionSort; var m: word; x: word; begin

x := a[i]; m := i-k; if s = 0 then s := - k; inc(s); a[s] :=x; while x < a[m] do begin a[m + k] :=a[m]; m := m - k end; a[m + k] := x end;

Для обчислення кроків, які використовуються для визна-чення підпослідовностей, де відбувається сортування включен­иям, використовується масив h. Для л = 20 000 він міститиме 9 елементів, а для п = 30 000 - усього 10. Значения елементів цього масиву можуть описуватися типом word. Частина основ-ної програми, що реалізує алгоритм методу Шелла з бар'єрами, виглядатиме так:

h_new := 1; count := 0; while h new <= n do begin

inc(count); h_old := h_new; h_new := 3 * h_old + 1; end; h[1]:=h_old; for i := 2 to count do

h[i]:=(h[i-1]-1)div3; forj := 1 to count do begin

k:=h[j];s:=-k; for i := k + 1 to n do InsertionSort; end;

Повний аналіз сортування методом Шелла дуже складний і доводиться на рівні математичного аналізу. Саме так Д. Кнут до-вів, що в найгіршому випадку при обраних значениях кроку я складність алгоритму становить 0(л^3/2), а при виборі залежності кроку h_k = 2h_k_, + 1 - 0(п^6/5). Зрозуміло, що це краще, ніж 0(п²).

Тестування алгоритму, що реалізує метод Шелла, треба провести на таких вхідних даних:

165

• вхідний масив уже впорядкований необхідним чином;

• вхідний масив є частково впорядкованим;

• вхідний масив упорядкований у зворотному порядку;

• елементи вхідного масиву розміщені випадковим чином. При цьому передбачити різні за довжиною масиви: п = 10,

п = 100, п = 1000, п = 10 000, п = 30 000.

/ Запитання для самоконтролю

1. На якому методі базується сортування методом Шелла?

2. У чому полягає ідея сортування масиву методом Шелла?

3. Наведіть приклад масиву та продемонструйте схематично ро­боту алгоритму сортування методом Шелла.

4. За якими алгоритмами Д. Кнут запропонував визначати кроки для поділу заданого масиву на групи гид час сортування?

5. Запишіть у вигляді процедури мовою Pascal фрагмент алго­ритму сортування масиву методом прямого включения.

6. Запишіть алгоритм сортування масиву методом Шелла у вигля-ді тексту Pascal-програми. Прокоментуйте роботу окремих бло-ків цього алгоритму.

7. За яким алгоритмом можна визначити максимальне значения h кроку поділу масиву, що складається з п елементів?

8. Якою є оцінка ефективності роботи алгоритму сортування маси­ву методом Шелла?

Завдання

1. Реалізувати у вигляді прогреми алгоритм сортування за­дано! послідовності за зростанням методом Шелла.

2. Модифікувати алгоритм завдання 1 таким чином, щоб сортування відбувалося за спаданиям.

3. Протестувати реалізовані в завданнях 1-2 алгоритма для масиву 15, 4, 10, 8, 6, 9, 16, 1, 7, 3, 11, 14, 2, 5, 12, 13.

4. Протестувати реалізовані у завданнях 1-2 алгоритми для масиву 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1.

1. Проаналізувати покрокове виконання завдань 3—4.

5. Підібрати власні тести, які доводять переваги й показу-ють недоліки сортування масивів методом Шелла при п > 100.

6. Порівняти результати роботи алгоритму сортування ме­тодом Шелла та алгоритму метода прямого включения для зав-дань 3—6.

2. Зробити письмовий аналіз завдань 3-7.

Пірамідальне сортування, або сортування деревом

Наступний алгоритм, який розглянемо як удосконалений, базується на методі сортування масиву за допомогою прямого вибору і побудований на відшуканні на кожному кроці най-меншого (або найбільшого) значения. У літературі цей метод

166

зустрічається шд назвою «пірамідальне сортування», «сорту -вання деревом», або «сортуваннякупою». Чому цетак, розгля-немо на відомому нам уже прикладі масиву:

44, 55, 12, 42, 94, 18, 06, 67.

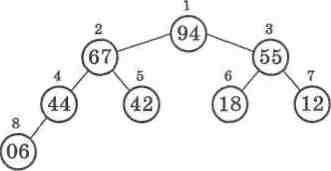
Що таке бінарне дерево, ми вже знаємо. Тому давайте пред-ставимо заданий масив саме у вигляді такого дерева (мал. 58), позначаючи кожну його вершину порядковим номером даного елемента у заданому масиві.

Мал. 58

На перший погляд нічого закономірного в цьому дереві не видно. Елементи розташувалися в ньому по рівнях так само, як у збалансованому дереві.

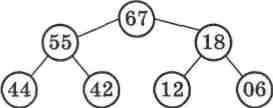
А тепер давайте представимо у вигляді бінарного дерева (мал. 59) той самий масив, відсортований у порядку спадання: 94, 67, 55, 44, 42, 18, 12, 06.

Мал. 59

Тепер, порівнюючи малюнки 58 і 59, можна побачити, що елементи бінарного дерева, побудованого зі значень відсортова-ного масиву, мають таку ознаку: кожний елемент дерева не менший, ніж yci елементи, для яких він є батьківським. Крім того, індекси елементів масиву, які відповідають цим верши­нам дерева, мають чіткий взаємозв'язок. Якщо розглянути еле­мент масиву з порядковим номером і, то його безпосередніми нащадками у дереві будуть елементи масиву з номерами 2і - лі-вий нащадок і 2і + 1 - правий. 3 іншого боку, елемент масиву, який є батьківським для елемента з індексом і, буде мати ін-декс [i/2] (i div 2).

167

Бінарне дерево, для будь-якої вершини якого виконуються одночасно дві умови a_t > а_и та а_; > о_2і , називається піра-мідою, або бінарною купою.

Зрозуміло, що для термінальних вершин піраміди такі умо­ви не виконуються, оскільки у них не існує нащадків. 3 наведе-ного означения можна зробити логічний висновок, що у вер­шин! піраміди завжди буде найбільший елемент.

Упорядкований за спаданиям масив завжди утворює піра-міду! Це видно з малюнка 59. А чи це єдиний варіант піраміди, тобто бінарного дерева, що відповідає означению піраміди? Спробуємо перетворити початковии масив, зображении на малюнку 58, у піраміду.

Будемо робити це так: піднімаючись рівнями від терміналь-них вершин дерева до кореневої, будемо впорядковувати еле-менти, що знаходяться у вершинах, за правилами піраміди (мал. 60).

Д) е)

Мал. 60

За п'ять кроків ми перетворили бінарне дерево, зображене на малюнку 58, у піраміду, тобто для кожної вершини вико-

168

нується необхідна для існування піраміди умова. Згідно з цією умовою також можна стверджувати, що коренем піраміди завжди буде вершина, у якій розміщено найбільший за значен­иям елемент масиву.

Як же виглядає тепер перетворений масив? Запишемо зна­чения вершин отриманої піраміди (мал. 60, д) у вигляді маси­ву: 94, 67, 18, 44, 55, 12, 06, 42.

Давайте спробуємо відновити дії, зображені на бінарному дереві з перетворення його на піраміду, на самому масиві (мал. 61).

а)

I	2	3	4	5	6	7	8
44	55	12	42	94	18	06	67

o)| t	2	3	4	5	6	7	8
44	55	12	67	94	18	06	42

в)
	1	2	3	4	5	6	7	8
	44	55	18	67	94	12	06	42

r)

1	2	3	4	5	6	7	5
44	94	18	67	55	12	06	42

Д)

1	2	3	4	5	6	7	8
94	44	18	67	55	12	0G	42

e)

2 2	3	4	5	6	7	S
94 67	18	44	55	12	06	42

Мал. 61

kflMHTHKit, !' I'¹ *•' I

169

Який висновок можна зробити, аналізуючи перетворення масиву, зображеного на малюнку 61?

По-перше, наибольший елемент «піднявся» в корінь дерева, тобто на початок масиву. Тому надалі його можна запам'ятати і виключити з наступного перегляду масиву.

По-друге, на малюнку 60, г, д та малюнку 61, г, д видно, що, для того аби зберегти структуру піраміди, доводиться інколи виконувати декілька кроків, навіть якщо вершини, для яких це робиться, не є коренем дерева. Наприклад, після виконання обміну 44 ** 94 (мал. 60, г) виявилося порушення умови піра-міди у вершит з номером 2 (мал. 61, д). Для відновлення піра-міди треба було зробити ще один обмін 44 *» 67. Отже, можна зробити висновок: виконання обмінів відбувається від термі-нальних вершин до кореневої, але коли місце обміну в дереві визначене, то надалі обмін виконується від цієї вершини вниз у напрямі до термінальних вершин доти, доки не відновиться структура піраміди.

По-третє, є певна закономірність між індексами елементів масиву, які міняємо місцями. Аналізуючи піраміду, зображе-ну на малюнку 58, зазначали, що кожен і-ий елемент масиву, який знаходиться у вершині піраміди, мае нащадків із по-рядковими номерами у масиві 2і та (2і + 1) для і < [п/2]. Це можна спостерігати на малюнку 61: обмін відбувається саме між такими елементами у масиві 8*»4,6*»3,5**2,2**1.

До речі, якщо в наведеному прикладі методом прямого об-міну ми знаходили найбільший (або найменший) елемент за 8 порівнянь і обмінів, то в даному разі - за 4. Слід погодитися, що це досить значне удосконалення.

Як визначити, за яку кількість кроків можна підняти най-більший елемент у корінь бінарного дерева? Це залежить від глибини дерева, яке можна побудувати із заданого масиву. Наш масив утворив піраміду з 4 рівнями, тому проходження ними і є тією кількістю кроків k, які необхідні для отримання у вершині найбільшого елемента. Оскільки маємо справу з бі-нарним деревом, то кількість кроків можна визначити як мак-симальне k, для якого справедлива залежність 2* < га, збіль-шене на 1, бо в дереві є нульова вершина.

Повернемося до нашого алгоритму. Оскільки найбільший елемент масиву отримано, то доречно було б його десь окремо запам'ятати і застосувати описаний алгоритм побудови піра-міди та підняття найбільшого елемента у ньому в корінь дерева для тієї частини масиву, що залишилася.

На малюнках 62—69 зображено два основні моменти нашого алгоритму:

- побудову бінарного дерева для фрагмента масиву на дано­му крощ;

170

- «підняття» найбільшого елемента в корінь бінарного дере­ва шляхом побудови піраміди.

На зазначених малюнках будемо зображати покроково ро­боту описаного алгоритму як у вигляді піраміди, так і у вигля-ді послідовності елементів масиву. Це буде надалі корисним під час розбору реалізації алгоритму пірамідального сортування.

2	1	2	3	4	5	6	7	8		1	1	2	3	■/	5	6	7	8
а,	44	55	12	42	94	18	06	67		а,	94	67	18	44	55	12	06	42

Мал. 62

_©

1	1	2	3	4	5	6	7	8		j	/	2	3	4	5	6	7	8
а,	42	67	18	44	55	12	06	94		"	67	55	18	44	42	12	06	94

Мал. 63

І	1	2	3	4	5	6	7	8		<•	/	2	3	4	.5	6	7	8
а,	06	55	18	44	42	12	67	94		а,	55	44	18	06	42	12	67	94

Мал. 64

171

_@©@

^@©@

І	/	2	3	4	5	6	7	в		i	І	2	3	4	5	в	7	8
«,	.12	44	18	06	42	55	67	94		а,	44	42	18	06	12	55	67	94

Мал. 65

(06

І	1	2	3	4	5	6	7	8		1	і	2	3	4	5	6	7	8
at	12	42	18	06	44	55	67	94		а,	42	12	18	06	44	55	67	94
К									1ал. 6	6
®Ґ®%										Ог^ое)
@©@©@										@©@@@
:	1	2	3	4	5	6	7	8		і	1	2	3	4	5	6	7	8
а,	06	12	18	42	44	55	67	94		°,	18	12	06	42	44	55	67	94

Мал. 67

06

12

06

12)

^@©@@@@

І	1	2	3	4	5	6	7	8		і	1	2	3	4	5	6	7	8
а,	06	12	18	42	44	55	67	94		аі	06	12	18	42	44	55	67	91

Мал. 68

172

^{@©@@@@@ @©@@@@@©}

І	1	2	3	4	5	6'	7	8
а,	06	12	18	42	44	55	67	94

Мал. 69

А тепер перейдемо до узагальнення всього вищесказаного.

Метод, що базується на описаному вище алгоритмі, нази-ваеться HeapSort.

Подивимося на загальний вигляд бінарного дерева як на піраміду (мал. 70).

Мал. 70

Аналізуючи малюнок 70, неважно помітити таку закономір-ність:

h_i>h_2lTah_l>h_{2l + v}Rei = 1, 2, ..., [л/2].

3 малюнка 70 видно, що термінальними вершинами є ті, по­рядков! номери яких у масиві більші за [л/2]. Усім іншим еле-ментам масиву в бінарному дереві відповідають вершини, які мають нащадків. Тому згідно з нашим алгоритмом будувати піраміду треба для елементів масиву з індексами і - [л/2], [л/2] - 1,..., 2, 1. Саме в такій послідовності треба переглядати елементи масиву на кожному етапі, включати їх у бінарне дере­во і будувати одночасно піраміду.

Визначаючи дерево як піраміду, слід констатувати, що Aj = max (л,, h₂,..., h_n). Але аналогічно елемент h₂ є найбільшим для свого піддерева, а л₃ - для свого. А це означав, що при ви-лученні (згідно з нашим алгоритмом) для наступного перегля­ду найбільшого елемента масиву, який знаходиться в корені побудованої піраміди, для подальшого збереження властивос-тей піраміди в бінарному дереві кількість переставлень якщо не зменшуеться, то явно не збільшується.

Отже, підіб'ємо підсумок наших міркувань у вигляді словесно­го алгоритму. Фактично цей алгоритм складається з двох кроків:

173

• побудувати піраміду для тієї частини масиву, яка розгля-дається на даному кроці;

• поміняти місцями найбільший елемент, який знаходиться в корені дерева, з останнім елементом тієї частини масиву, що розглядається, та зменшити з кінця кількість елементів маси­ву, частина якого розглядається.

Реалізуємо цей алгоритм мовою програмування Pascal.

Спершу розглянемо процедуру, яка реалізує переміщення поточного L-го елемента масиву на свое місце в піраміді. Це здійснюється шляхом порівняння його значения зі значениями безпосередніх нащадків. Якщо серед нащадків є більший за по-точний елемент, то піднімаємо його на місце поточного і визна-чаємо цього нащадка поточним елементом. Процес завер-шується в одному з таких двох випадків: або ми дійшли до тер-мінальної вершини, або обидва нащадки менші за поточний елемент. Отже, процедура pyramida будує піраміду з елементів масиву a_L, ..., a_R.

procedure pyramida (L, R: word); var i, j: word; x: word;

begin {Запам'ятовуємо значения вершини,)

X := а[Ц; {яке необхідно поставити на свое місце в піраміді.)

i := L; {Визначаємо цю вершину поточною.)

j := 2 * L; {Визначаємо лівого нащадка для поточної вершини.)

{Якщо існує правий нащадок для поточноі вершини)

if (j<R) and (a[j + 1] > a[j]) {i він більшийзалівого,)

then j := j + 1; {то переходимо до нього.)

{Переглядаємо всіх нащадків, які більші за поточний елемент.)

while (j <= R) and (a[j] > x) do

begin

{Якщо нащадок більший за поточний елемент,)

a[i] := a[j]; {то переміщаємо його на місце поточного.)

І := j; {Переходимо до нащадка як до поточного елемента.)

j := 2 * j; {Визначаємо для поточного елемента його нащадка.)

{Якщо існує правий нащадок для поточно! вершини)

if (j<R) and (a[j + 1] >a[j]) {i він більший за лівого,)

then j := j + 1 {то переходимо до нього.)

end;

а[І] := X {Ha місце поточно! вершини записуємо значення елемента а[Ц.)

end;

Тепер основна частина алгоритму виглядатиме так:

L := (n div 2) + 1; R := п; {Визначимо термінальні вершини.)

{Формування стартової піраміди із заданих п елементів масиву.) while L > 1 do begin

L := L - 1; {Переміщення L від (n div 2) + 1 до 1.)

{Включения кожного L-го елемента масиву в піраміду.) pyramida (L, R) end;

174

while R > 1 do {Перегляд фрагментів масивуа[1] a[R].)

begin

x:=a[1]; a[1] :=a[R]; a[R] :=x; {Обмінмісцямиелементіва[і]іа[Я].} R := R - 1; {Зменшення довжини масиву з кінця.} pyramida (1, R) {Побудова піраміди для фрагментів масиву а[1] а[Я].}

end;

Аналіз алгоритму пірамідального сортування полягає у визна-ченні середньої кількості дій, що їх треба виконати для здійснен-ня сортування будь-якого масиву за допомогою цього методу.

Раніше зазначалося, що даний алгоритм складається з двох частин: побудова піраміди для фрагмента масиву та вилучення найбільшого елемента, який з'явився у корені бінарного дерева.

Із цих міркувань можна визначити оцінку ефективності ви-користання методу пірамідального сортування. Рух по бінарно-му дереву будь-якого елемента для побудови піраміди стано-вить 0(log₂n). Але оскільки цю процедуру треба виконати для всіх п елементів масиву, то остаточна оцінка даного методу ста-новить 0(п log₂n).

Оскільки метод пірамідального сортування належить до удосконалених методів, то результати його тестування повин-ні відповідно це продемонструвати. Рекомендується підібрати такі вхідні дані:

• вхідний масив уже впорядкований необхідним чином;

• вхідний масив є частково впорядкованим;

• вхідний масив упорядкований у зворотному порядку;

• елементи вхідного масиву розміщені випадковим чином. При тестуванні передбачити п = 10, п = 100, п = 1000,

п = 10 000, п = 30 000.

/ Запитання для самоконтролю

1. На якому методі прямого сортування базується метод піра-мідапьного сортування?

2. Зобразіть одновимірний масив у вигляді бінарного дерева, ви-користавши для цього власний приклад.

3. Як виглядатиме бінарне дерево, побудоване з того самого масиву, що й у запитанні 2, але після його упорядкування за спаданиям?

4. Які характерні ознаки можна відмітити, порівнюючи бінарні де­рева у запитаннях 2-3?

5. Яке бінарне дерево можна називати пірамідою, або бінарною купою?

6. Що можна сказати про значения елемента, який знаходиться в корені піраміди?

7. Продемонструйте на власному прикладі перетворення будь-якого бінарного дерева на піраміду, зобразивши цю інформацію як у вигляді дерева, так і у вигляді масиву.

175

8. Які три основні висновки можна зробити, аналізуючи виконання запитання 7?

9. Як можна визначити, за яку кількість кроків можна підняти най-більший елемент у корінь бінарного дерева?

8. Зобразіть поетапно на власному прикладі алгоритм сортування за допомогою побудови бінарного дерева та підняття найбіль-шого елемента вгору шляхом побудови піраміди.

9. Яка існує залежність між індексами елементів масиву, які є тер-мінальними вершинами у відповідному бінарному дереві?

10. Яка існує залежність між елементами масиву, з яких можна утво-рити піраміду, зберігаючи їх послідовність у масиві?

11. Сформулюйте словесний алгоритм сортування одновимірного масиву методом пірамідального сортування.

12. Запишіть у вигляді фрагмента Pascal-програми алгоритм піра-мідального сортування.

13. Поясніть окремі фрагменти Pascal-програми, наведено! у запи-танні 14, та їх призначення.

14. Якою є оцінка ефективності роботи алгоритму пірамідального сортування? Обґрунтуйте свою відповідь.

Завдання

1. Реалізувати у вигляді програми алгоритм сортування за­дано! послідовності за зростанням методом пірамідального сор­тування.

2. Модифікувати алгоритм у завданні 1 так, щоб сортування відбувалося за спаданиям.

3. Протестувати реалізовані в завданнях 1—2 алгоритми для масиву 15, 4, 10, 8, 6, 9, 16,1, 7, 3, 11,14, 2, 5,12, 13.

4. Проаналізувати покрокове виконання завдання 3 щодо кількості виконуваних дій.

5. Шдібрати власні тести, які доводять переваги й показують недоліки методу пірамідального сортування при п > 100.

6. Зробити письмовий аналіз завдань 3—5.