Рекурсивний бінарний пошук

У класичній літературі, що розглядає питания алгоритмі-зації, рекурсивні алгоритми ще називаються алгоритмами з поверненням.

114

Для пояснения використання рекурсивності в пошукових алгоритмах сформулюємо таку задачу.

Нехай автомат, який щохзилини виготовляє деталі, мае пристрій, що фіксує їх виготовлення та виводить на друк від-повідний протокол. Якщо протягом робочої зміни автомат працював без збоїв, то порядковий номер останньої виготов-леної деталі збігатиметься з останніми числовими даними про­токолу. Але пристрій був не дуже якісний і в деякі моменти часу його «заїдало». Тому фіксація нових виготовлених де­талей тимчасово припинялася і в протоколі повторювалося значения порядкового номера останньої деталі перед збоєм. Через деякий час робота пристрою сама собою відновлювалася і лічба виготовлених деталей продовжувалася, починаючи з останнього зафіксованого значения. У результаті дані при­строю наприкінці зміни не збігалися з реальною кількістю виготовлених деталей.

Необхідно розробити алгоритм, який би визначав, у які хви-лини пристрій працював некоректно.

Наведемо приклад. Якщо дані пристрою під час виготовлен­ня 10 деталей були такими:

122344456 7,

то можна зробити висновок, що збої пристрою відбувалися на 3-й, 6-й і 7-й хвилинах.

Ознакою відсутності збою між двома сусідйіми значениями є виконання умови a[k + 1] - a[k] = 1, а між /г-им та Z-им значен­иями відповідно (k < I) а[1] - a[k] - I - k.

Якби було відомо, що під час роботи пристрою відбувся ли­ше один збій, то його пошук можна було б здійснити за допомо-гою алгоритму бінарного пошуку. Цей алгоритм за зазначених вище умов виглядатиме так:

L:=1;R:=N; while (L<R) do begin

m:=(L+R)div2; if a[m] - a[L] = m - L then L := m + 1 else R := m end; if a[R] = x then writeln ('Шуканий елемент знайдеио')

else writeln ('Шуканий елемент не знайдено');

Однак цей алгоритм не буде коректно працювати в разі кіль-кох збоїв пристрою. А саме якщо збої будуть як у правій, так і в лівій частині задано!' послідовності, то, відкидаючи одну з них згідно з алгоритмом бінарного пошуку, ми тим самим не

115

матимсмо змоги ііадолі визначити всі збої. Щоб на настуПНИХ кроках перегляду заданої послідовності збоїв була можливість поверыутися до тих її частин, що відкидаються методом бі-нарного пошуку, треба застосувати рекурсивне повернення до них на наступних кроках алгоритму.

Отже, зробимо висновок: для того щоб визначити всі збої системи, використовуючи алгоритм бінарного пошуку, треба організувати рекурсивне звернення до всіх ділянок заданої по-слідовності, застосувавши для кожної з них алгоритм бінарно-го пошуку.

Рекурсивна процедура, що здійснює пошук збоі'в системи в послідовності даних, може бути такою:

procedure Bin_Recur (L, R: byte); var m: byte; begin

ifL+1 OR then begin

m:=(L+R)div2;

if a[m] - a[L] <> m - L

then BinRecur (L, m); if a[R] - a[m] <> R - m then Bin_Recur (m, R); end else writein (f_out, R) end;

Виклик процедури для послідовності з п елементів буде та­ким: Bin_Recur(l, n).

Проаналізуємо деякі фрагмента наведено!' процедури ре­курсивного пошуку.

Мабуть, у вас відразу ж виникло запитання щодо параметрів виклику рекурсивно']' процедури для лівої Bin_Recur(L, m) i правої' Bin_Recur(m, R) частин поточного проміжку. Справді, на відміну від наведеного вище алгоритму, який розглядає ли­ше один збій нашої лічильної системи, у даному випадку гра-ничний елемент з номером т включається як у праву частину, так і в ліву. Це пояснюється тим, що в нашій задачі необхідно весь час контролювати два сусідні елементи. Розглянемо такий конкретний приклад. У випадку послідовності 12 2 2 3 відразу видно, що збої відбулися на 3 та 4 кроках. Центральним еле-ментом цієї послідовності при т = 3 буде а[3] = 2. Якщо ж ми поділимо дану послідовність на такі дві частили: 1 2 2 і 2 3, то аналіз лівої дасть відповідь 3, а правої не визначить жодних збої'в. Таким чином, на цьому прикладі добре видно, що цент-ральний елемент необхідно включати як у праву, так і в ліву частини при поділі навпіл поточної послідовності.

116

Ще одне питания може виникнути щодо умови продовжепня виклику рекурсивного пошуку L + 1 о R, оскільки в по-передньому варіанті бінарного пошуку ця умова виглядала так: L < R. Чим це пояснюється? Справа в тому, що в задачі бінарно-го пошуку одного елемента в заданій послідовності ми ділили навпіл нашу послідовність до того часу, поки не зупинилися на одному елементі, що визначалося саме умовою L < R. У задачі рекурсивного бінарного попіуку кількох шуканих елементів ми повинні зупинитися на двох сусідніх елементах і проана-лізувати їхні значения, звужуючи при цьому проміжок, що розглядається. Таким чином, номери лівого і правого елемен-тів відрізнятимуться на 1: L + 1 = R.

Проведемо порівняльний аналіз алгоритму звичайного бі-нарного пошуку та рекурсивного бі парного пошуку.

Зрозуміло, що перший із них дуже ефективно знаходить лише один необхідний елемент у заданій послідовності. Тому в такому випадку немає потреби в застосуванні рекурсивності.

У разі, коли шуканих елементів у послідовності може бути декілька, то виникає потреба у перегляді всіх частин послідов-ності. Звичайний алгоритм бінарного пошуку, на жаль, такої можливості не надає, оскільки завжди відкидає одну з двох частин поточної послідовності. Тому в такому випадку може допомогти лише рекурсивний перегляд усіх частин послідов-ності. Але й у цьому разі треба знати міру. Наприклад, коли шуканих елементів у послідовності дуже багато і сама послі-довність велика, то рекурсивний алгоритм може «захлинути-ся»: не вистачить стекової пам'яті для розміщення незавер-шених рекурсивних процедур. Та й щодо часу виконання рекурсивного алгоритму є проблеми: треба визнати, що рекурсивний виклик потребуе додаткового часу. Тому у випад­ку, коли в задачі передбачається наявність великої кількості шуканих елементів у великій послідовності, то варто застосу-вати звичайний лінійний пошук.

Отже, можна зробити висновок. Використання рекурсивно­го бінарного пошуку доцільне лише після детального аналізу поставлено!' задачі та характеру можливих вхідних даних.

3 огляду на проведений аналіз алгоритму рекурсивного бі-нарного пошуку визначимо оцінки його ефективності. На ма-люнку 37 зображено дерево пошуку розв'язку задачі для п = 8. У термінальних вершинах дерева вказані самі елементи меси­ву, серед яких можуть бути шукані елементи. В інших вер­шинах дерева вказано рівень поділу задачі на підзадачі: у ко-реневій - 1, оскільки це перший поділ, у наступних - 2, бо на цьому рівні йде поділ ще на дві підзадачі і т. д.

117

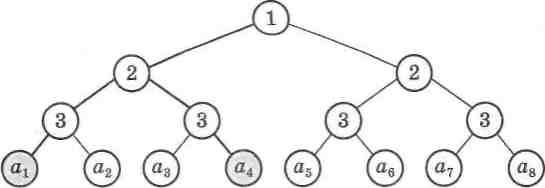
Мал. 37

Для найкращого випадку, коли кількість шуканих елемен-тів k у масиві значно менша, ніж самих елементів масиву п, тобто k « п, то оцінкою буде величина 0(log₂n) + С{п) + D(n).

Для випадку наявності двох шуканих елементів у вхідному масиві, тобто при k = 2 (на мал. 37 ці елементи виділено), мож-на зробити такі обчислення. До елемента а_л можна дійти за log₂n кроків, до елемента а₄ - за log₂(n/2) кроків, оскільки до нього можна прийти, повернувшись на рівень 2. Тому отри-маемо результат обчислення:

log₂n + log₂(ra/2) = log₂n + log₂n - log₂2 = 21og₂n -1 - log₂n.

Тобто за наявності невелико!' кількості шуканих елементів у заданому масиві оцінка даного алгоритму залишається 0(log₂n) + С(га) + D(n).

У найгіршому випадку, тобто коли таких елементів багато, тобто k - п, оцінкою буде О(п) + С(п) + D(n), оскільки за алго­ритмом визначення оцінки роботи рекурсивних алгоритмів треба обчислити кількість викликів підзадач, на які буде поділено задачу. Таких поділів буде - п. Як бачимо, додаткові затрати часу на поділ задачі на підзадачі під час виклику ре­курсивних процедур і об'єднання отриманих результатів робо­ти рекурсивних процедур у кінцевий результат мають зміст ли­ше при великих п і малих k.

/ Запитання для самоконтролю

1. Сформулюйте задачу пошуку необхідної інформаціі в заданій групі значень, використовуючи рекурсивність.

2. Як можна застосувати алгоритм бінарного пошуку у випадку, ко­ли шукана інформація у сформульованій задачі присутня у за-даній послідовності лише один раз?

3. Обґрунтуйте некоректність роботи алгоритму бінарного пошуку для випадку існування кількох шуканих елементів у заданій по-слідовності.

4. Чому рекурсивний алгоритм бінарного пошуку вирішує проб­лему, поставлену в попередньому запитанні? Обґрунтуйте свою відповідь.

118

5. Запишіть алгоритм і текст Pascal-програми рекурсивного бі-нарного пошуку.

6. Як можна здійснити виклик рекурсивно! процедури бінарного пошуку з тіла основної програми?

7. Чим пояснюеться включения граничного елемента а[т] при поділі поточної послідовності на дві частини у перегляд як лівої, так і право! частин, що надалі досліджуватимуться?

8. Поясніть умову завершения рекурсивного пошуку L + 1 О R. Обґрунтуйте свою відповідь.

9. Коли використання алгоритму рекурсивного пошуку є ефектив-ним?

10. Коли використання алгоритму рекурсивного пошуку може стати неефективним?

11. Оцініть умови ефективності використання лінійного й рекурсив­ного бінарного пошуків декількох шуканих елементів у великій послідовності заданих елементів.

12. Якою є оцінка ефективності роботи рекурсивного бінарного пошукового алгоритму?

Завдання

1. Розробити й реалізувати алгоритм бінарного рекурсивно­го пошуку збоїв системи підрахунку виготовлених деталей.

2. Виконати завдання 1 для .N=10:1112345678. Визна­чити, скільки рекурсивних викликів процедури бінарного по­шуку використано для отримання відповіді.

3. Виконати завдання 1 для N •= 10: 123456788 8. Визна­чити, скільки рекурсивних викликів процедури бінарного по­шуку використано для отримання відповіді.

4. Виконати завдання 1 для N = 10: 123444567 8. Визна­чити, скільки рекурсивних викликів процедури бінарного по­шуку використано для отримання відповіді.

5. Виконати завдання 1 для N = 50 і для рівномірно роз-поділених збоїв системи в заданій послідовності. Визначити, скільки рекурсивних викликів процедури бінарного пошуку використано для отримання відповіді.

5. Зробити порівняльний аналіз завдань 2-5.

5. Виконати завдання 1 для N ■ 10: 1111111111. Визна­чити, скільки рекурсивних викликів процедури бінарного по­шуку використано для отримання відповіді.

6. Виконати завдання 7, використавши алгоритм лінійного пошуку.

7. Провести аналіз виконання завдань 7-8 щодо ефективнос-ті використання рекурсивного алгоритму.

10. Виконати завдання 7-9 для N = 1000.

119

ПОШУКОВІ АЛГОРИТМИ НА БІНАРНИХ ДЕРЕВАХ

Задача про частотний словник

Розглядаючи структуры даних, ми вже ознайомилися з та­кою структурою, як дерево:

type Prt = ^ANode; Node = record

data: <тип > ; left, right: Prt; end;

Нагадаємо, що дерево пошуку будується за такою ознакою: лівим нащадком для кожного числа у вершині дерева буде мен-ше за нього число, а правим - більше.

Ми ознайомилися також із тим, яким чином у дереві відбу-вається читання та запис інформації.

Однією з найпоширеніших задач, яка супроводжує виконан-ня операцій на деревах, є «обхід» дерева. Прикладом такої за­дач! є процедура друкування дерева, яка наводилася раніше, коли розглядалася структура даних «дерево».

Ще одна задача - пошукова, або, як ще кажуть, пошук за унікальним ключей. Спираючись на принцип побудови дерева пошуку, рух по ньому можна здійснювати від кореня по лівому або правому піддереву лише на підставі одного порівняння з ключей поточної вершини:

function locate (х: integer; t: Prt): Prt; begin

while (t <> nil) and (t\key <> x) do if t".key<x then t :=t\right else t := r.left; locate := t end;

Зрозуміло, що, в разі відсутності ключа в дереві, отримаємо результат locate (х, t) := nil.

Зауважимо, що висота дерева, яке складається з п вершин, не буде перевищувати log₂n.

Доповнимо всю згадану інформацію про бінарні дерева ще однією задачею, яка в літературі носить назву «частотного словника», або «пошуку по дереву з включениям». Якщо рані-ше ми розв'язували подібні задачі на вже побудованих деревах, то ця задача розглядає ситуацію, коли дерево постійно росте.

Умова задачі полягає в тому, щоб у наперед заданій послі довності визначити частоту входження кожного елементг (ключа). Це означав, що будь-який елемент треба шукати в де реві, причому вважаючи, що початковий стан дерева — по

120

рожнє дерево. Якщо елемент знайдено, то лічильник його вхо-джень збільшується, якщо ж ні, то цей новий елемент вклю-чається у дерево з початковим значениям лічильника 1.

Згідно з умовою задачі дещо змінимо тип, який описує дере­во пошуку із включениям:

typeWprt = "Node; Node = record

data: <тип > ; count: word; left, rigth: Wprt; end;

Як бачимо, зміни відбулися у структурі елементів, 3 яких складається дерево. 3'явилося ще одне поле count - лічильник входження відповідного елемента в задану послідовність.

Процедура search повинна бути організована таким чином, що коли пошук заходить у «глухий кут» (піддерево - nil), то у цьому разі відбувається включения на це місце значения х.

procedure search (х: integer; var р: Wprt); begin

if p = nil then

begin new (p); with p^A do begin

key := x; count := 1; left := nil; right := nil; end; end else

if x<p^A.key then search (x, pMeft)

else if x > p\key then search (x, p\right)

else p^A.count := p\count + 1 end;

Нехай root - змінна, що означає корінь дерева. Тепер фраг­мент програми, за допомогою якого інформація читається із вхідного файла і, за необхідності, включається в дерево, мати-ме такий вигляд:

read (f, х); while not eof (f) do begin

search (x, root); read (f, x) end;

Для виведення вмісту побудованого дерева на екран монітора можна використати процедуру PrintTree (root, 0), що наводила-ся раніше при ознайомленні зі структурою даних «дерево».

121

Спочатку для прикладу розглянемо таку послідовність да-них, що містяться у файлі та трапляються в ньому лише один раз:

21,8,9,11,15,19,20,21, 7,3,2,1, 5,6,4,13,14,10,12,17,16,18.

Згідно з нашою програмою першим елементом є значения п, а далі розміщені елементи заданої послідовності. Дерево по-шуку матиме такий вигляд (мал. 38):

Мал. 38

Тепер розглянемо приклад послідовності елементів, серед яких е повтори значень. Наприклад:

21,8,9,13,15,19,10,21, 7,13,2,1,5,16,4,15,14,10,12,8,16,18.

При побудові дерева пошуку біля кожного елемента будемо визначати кількість його повторень у заданій послідовності (мал. 39).

Підіб'ємо деякі підсумки розглянутого пошукового алгоритму.

По-перше, основна ідея даного алгоритму базується на вико-ристанні структури даних «дерево».

По-друге, саме використання цієї структури дає змогу до-сить компактно зберігати в пам'яті вхідну інформацію, що по-дібна до алгоритмів «стиснення», оскільки в такому дереві від-сутні повтори одних і тих самих елементів.

По-третє, pyx побудованим деревом під час пошуку необхід-ного елемента значно швидший, аніж лінійно по масиву.

122

Мал. 39

Однак слід зазначити, що остання перевага мае сенс лише у випадку, коли треба здійснювати багатократний пошук зада-ного елемента у послідовності. Тоді варто лише один раз побу-дувати дерево, а потім протягом виконання алгоритму здійс-нювати пошук необхідну кількість разів. Якщо ж пошук відбу-вається одноразово, то його можна організувати лінійно під час читання самої послідовності значень і одночасно рахувати кількість входжень шуканого елемента у цю послідовність.

Оцінка ефективності використання дерева пошуку для ви-значення наявності шуканого елемента х у заданій послідов-ності а[і], і = 1, 2, ..., п складає 0(log₂n). Таку формулу можна пояснити тим, що на кожному кроці шлях пошуку змен-шується вдвічі і вибирається один із двох можливих варіантів руху по дереву.

• Запитання для самоконтролю

1. Опишіть структуру даних, яка визначає дерево.

2. Яке дерево називаеться деревом пошуку?

3. Запишіть алгоритм обходу дерева.

4. Запишіть алгоритм пошуку елемента в дереві за унікальним ключем.

5. У чому полягає сутність задачі, що носить назву «частотний словник»?

6. Опишіть структуру дерева, що визначаеться постановкою зада-чі частотного словника.

7. Запишіть алгоритм І текст Pascal-процедури включения нового еле­мента х у дерево пошуку для реалізації задачі «частотний словник».

8. Як можна використати описану в попередньому пункті проце­дуру для побудови частотного словника?

9. Запишіть алгоритм І текст Pascal-процедури виведення на екран монітора вмісту побудованого дерева пошуку для реалізації за­дач! «частотний словник».

10. Наведіть свій приклад послідовності елементів і зобразіть гра-фічно дерево пошуку, що відповідає цій послідовності.

123

I

11. У чому полягають переваги використання структури даних «дерево» для пошуку необхідної інформаці? в заданій послідов-ності елементів?

12. Якою є оцінка ефективності роботи лінійного пошукового алго­ритму? Обґрунтуйте свою відповідь.

Завдання

1. Розробити й реалізувати алгоритм побудови частотного словника.

2. Виконати завдання 1 для послідовності з 10 різних еле-ментів, вивівши на екран монітора вміст побудованого дерева.

3. Виконати завдання 1 для послідовності з 10 елементів, се­ред яких є значения, що повторюються. Вивести на екран мо­нитора вміст побудованого дерева.

4. Виконати завдання 1 для послідовності з 1000 елементів, серед яких є значения, що повторюються. Вивести на екран мо-нітора вміст побудованого дерева.

5. Проаналізувати ефективність виконання алгоритму побу­дови частотного словника для багатократного пошуку різних елементів, використовуючи завдання 4. Для визначення ефек-тивності роботи алгоритму підраховувати кількість вершин, які необхідно пройти для визначення результату.

6. Виконати завдання 4-5, використовуючи алгоритм ліній-ного пошуку.

7. Порівняти ефективність алгоритмов у завданнях 4-5 та в завданні 6.