Сортування обміном

Алгоритм, що застосовує метод обміну для сортування од-новимірного масиву, ще називають «бульбапіковим». Це пояс-нюється тим, що на кожному кроці алгоритму розглядаємо, починаючи з кінця до початку, два сусідні елементи і міняємо їх місцями у випадку, якщо правий елемент менший за лівий. При цьому відбувається «виштовхування» найлегшого (най-меншого) елемента в початок масиву.

Реалізація алгоритму у вигляді програми буде такою:

for i := 2 to n do

for j := n downto i do ifaD-1]>a[j] then begin

| x:=a[j-1];a[j-1]:=a[j];a[j] :=x end;

Наприклад, розглянемо той самий масив 44, 55, 12, 42, 94, 18, 06, 67. На першому кроці, розглядаючи його від кінця до початку, будемо переміщувати найменший елемент на перше місце. Це буде число 06.

У результаті виконання внутрішнього циклу отримаемо пе­ретворений масив 06, 44, 55, 12, 42, 94, 18, 67. Тепер вступав в

152

роботу зовнішній цикл. Він «скорочує» масив, оскільки най-менший елемент уже стоїть на своему місці. У внутрішньому циклі розглядатимемо масив 44, 55, 12, 42, 94, 18, 67. У ре­зультат! роботи внутрішнього циклу наймеиший його елемент стане на свое місце (у початковому масиві це буде друге місце). Отримаємо такий проміжний результат сортування: 12, 44, 55, 18, 42, 94, 67. Цей процес продовжуватиметься доти, доки на останньому кроці не буде (за необхідності) здійснено обмін двох останніх елементів.

Описаний вище процес наочно представлений у вигляді таб-лиці 16, де масив розміщено у стовпчиках, аби змоделювати виштовхування «найлегших» (найменших) елементів масиву угору.

Таблиця 16

1	2	3	4	5	6	7	8
44	06	06	06	06	06	06	06
55	44	12	12	12	12	12	12
12	55	44	18	18	18	18	18
42	12	55	44	42	42	42	42
94	42	18	55	АА	44	44	44
18	94	42	42	55	55	55	55
06	18	94	67	67	67	67	67
67	67	67	94	94	94	94	94

ІСлід звернути увагу на те, що протягом виконання внут-рішнього циклу, в якому здійснюється обмін двох сусідніх еле-ментів масиву, відбувається не лише «виштовхування» най-меншого елемента, а й поточне переставлення інших елемен-тів, які в такий спосіб також повільно пересуваються до своїх

I остаточних місць. Наприклад, у стовпчику 3 елемент 12 не лише став на свое остаточне місце, але й змінив свое положен­ия відносно інших елементів елемент зі значениям 18, про­сунувшись уперед. Так само у стовпчику 4 помінялися місцями (елементи 94 і 67, хоча на цьому кроці відбувалося просування на свое остаточне місце елемента 18. Сортування включениям Розглянемо задану послідовність a_v а₂,..., а_п. Відомо, що на t-му кроці а_х, а₂, ..., а_(-1 - упорядкована частина послідовності. Ідея алгоритму цього методу полягае в тому, що для кожного і - 2, 3, ..., п елемент а[і] ставиться в упорядковану частину

153

послідовності, що йому передує, на свое місце. Для реалізації цього алгоритму треба розширити проміжок зміни індексів ма-сиву: var a: array[0..100] of real;. У вигляді фрагмента программ цей алгоритм буде таким:

for І := 2 to n do begin

{a[0] - граничний елемент масиву, на якому зупиниться цикл} {у разі, коли переміщуваний елемент є найменшим у масиві.} x:=a[i];a[0] :=x;j:=i; while x< a[j — 1] do begin

a[fl:=a0-1];

j:=j-1 end; a[j]:=x end;

Розглянемо алгоритм на тому самому прикладі масиву: 44, 55, 12, 42, 94, 18, 06, 67 (табл. 17). Таблицю (так само як і для демонстрації роботи методу вибору) розмістимо по рядках.

Таблица 17

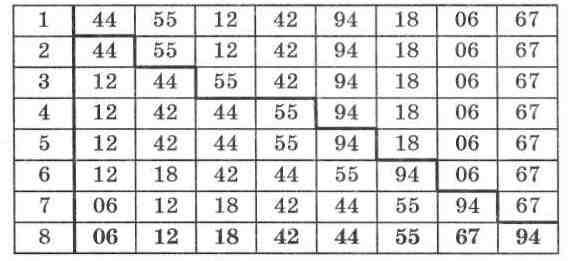
Зовнішній цикл на кожному кроці буде «зсувати» початок масиву, що розглядається у внутрішньому циклі. Спочатку це буде весь масив, потім, починаючи з другого елемента, далі - а третього і т. д. Зараз нас цікавитиме, що відбувається у внут-рішньому циклі, як визначається місце для найменшого еле­мента на даному кроці. Мабуть, ви вже помітили, що в цьому прикладі алгоритму внутрішній цикл організований як цикл із передумовою. Справа в тому, що якщо вже знайдено місцезна-ходження елемента, що ставиться на свое місце, то немае сенсу продовжувати перегляд масиву далі.

154

Отже, проаналізуємо алгоритм. Для кращого розуміння ро­бота алгоритму варто вручну виконувати покроково всі наступ-яі дії.

На першому кроці зовнішнього циклу встановлюються такі значения змінних: і = 2, х := а[2] (х = 55), а[0] = 55, j := 2. При-значення штучно введеного елемента масиву а[0] побачимо піз-ніше. Умова внутрішнього циклу не справджуеться (55 < 44), тому все лишається на своїх місцях.

На другому кроці зовнішнього циклу і = 3, х := а[3] (х = 12), а[0] - 12, j := 3. Починаемо виконувати внутрішній цикл. На його першому кроці умова справджуеться - 12 < 55. Заходимо всередину внутрішнього циклу і виконуемо присвоения: на трете місце в масиві ставимо число 55 (масив: 44, 55, 55, 42, 94, 18, 06, 67). Чи можна це робити, чи не пошкодимо масив? Hi, оскільки число, що було на третьему місці, тобто 12, ми запа-м'ятали у змінній х перед початком внутріпшього циклу. Змі-нюємо параметр внутрішнього циклу j := j - 1 (у = 2) i переходи­мо до наступного його кроку. Знову перевіряємо умову циклу. Тепер вона вже мае вигляд 12 < 44. Умова справджуеться, і то­му знову виконуемо внутрішній цикл, на друге місце в масиві ставимо число 44 (масив: 44, 44, 55, 42, 94, 18, 06, 67). На за­вершения цього кроку внутрішнього циклу j = 1. При повер-ненні на початок внутрішнього циклу вступае в роботу о[0], оскільки перевіряється умова д: < а(0] (12 < 12). Ця умова не виконується, і внутрішній цикл припиняе свою роботу. Але після його завершения в зовнішньому циклі є ще один оператор a[j] := х, який при поточних значениях змінних мае вигляд а[1] := 12. Тепер все стало на свої місця, і масив мае такий ви­гляд: 12, 44, 55, 42, 94, 18, 06, 67.

Не варто розглядати наступні кроки виконання зовніш-нього циклу, оскільки вони аналогічні. Можна зробити такий висновок:

Ь — на кожному кроці зовнішпього циклу поточний елемент ісиву, рухаючись уліво на початок масиву, «шукае» свое сце в уже відсортованій лівій частині;

- pyx поточного елемента вліво відбувається доти, доки не виконається умова, за якої поточний елемент більший або рівний елементу лівої частини масиву, тобто цей рух не завжди сятае першого елемента заданого масиву.

Насамкінець проаналізуємо наведені методы впорядкувапня одновимірних масивів. Критерієм оцінки визначимо кількість виконуваних дій (кроків циклу) для отримання результату.

3 цього погляду перші два методи мало чим відрізняються один від одного. Обидва використовують два вкладені цикли типу for ... to ... do. Тому кількість виконуваних повторень при виконанні цих циклів залежить від кількості елементів. Хоча

155

слід зазначити, що метод прямого обміну є ефективнішим, якщо масив не впорядкований. У випадку частково впорядко­ваного або майже впорядкованого масиву метод вибору мае значні переваги по кількості порівнянь.

Третій алгоритм, що реалізує метод прямого включения, суттєво відрізняється від перших двох, оскільки внутрішній цикл є циклом з передумовою while ... do. Кількість кроків цього циклу залежить від виконання умови х < a[j - 1]. А це означає, що він завершиться, коли ми знайдемо місце елемента х в уже впорядкованій лівій частині масиву. Тому метод вклю­чения слід використовувати, коли треба довпорядкувати май­же впорядкований масив.

Загалом оцінка всіх цих методів визначається як 0(п^г), оскільки в загальному випадку для виконання повного сорту-вання будь-якого масиву потрібно кожний його елемент порів-няти та, за необхідності, обміняти місцями з кожним іншим елементом.

При тестуванні прямих алгоритмів сортування необхідно перевірити коректність їх роботи на таких вхідних даних:

• вхідний масив уже впорядкований необхідним чином;

• вхідний масив є частково впорядкований;

• вхідний масив упорядкований у зворотному порядку;

• елементи вхідного масиву розміщені випадковим чином.

Крім цього, перевірка коректності роботи алгоритму по­винна бути досліджена на різних за довжиною масивах. На-приклад, при п - 10, п = 100, п - 1000, п - 10 000, л = 30 000.

/ Запитання для самоконтролю

1. Сформулюйте класичну задачу сортування одновимірного ма­сиву.

2. У чому полягає основне питания, що вирішується під час сорту­вання масиву?

1. За якими ознаками класифікуються методи сортування?

2. Як класифікуються методи сортування за методикою сортування"

3. Як класифікуються методи сортування за кількістю виконувани* операцій?

4. У чому полягає ідея алгоритму сортування методом прямого вибору?

5. Запишіть алгоритм і текст Pascal-програми, що реалізує сорту­вання одновимірного масиву методом прямого вибору.

6. Наведіть приклад масиву і заповніть таблицю, яка демонструе сортування цього масиву методом прямого вибору.

7. Виконайте покроково метод прямого вибору для сортування одновимірного масиву, використавши таблицю, наведену у за-питанні 8.

10. Які зміни необхідно зробити в алгоритмі, щоб сортування маси­ву за зростанням замінити на сортування за спаданиям?

156

11. У чому полягає ідея алгоритму сортування методом прямого об-міну?

12. Запишіть алгоритм і текст Pascal-програми, що реалізує сорту­вання одновимірного масиву методом прямого обміну.

13. Наведіть приклад масиву і заповніть таблицю, яка демонструе сортування цього масиву методом прямого обміну.

14. Виконайте покроково метод прямого обміну для сортування од-новимірного масиву, використавши таблицю, наведену у запи-танні 8.

15. У чому полягає ідея алгоритму сортування методом прямого включения?

16. Запишіть алгоритм і текст Pascal-програми, що реалізує сорту­вання одновимірного масиву методом прямого включения.

17. Наведіть приклад масиву і заповніть таблицю, яка демонструе сортування цього масиву методом прямого включения.

18. Виконайте покроково метод прямого включения для сортування одновимірного масиву, використавши таблицю, наведену у за-питанні 8.

19. Яким є удосконалення алгоритму сортування методом прямого включения?

20. Порівняйте методи сортування прямим вибором, обміном і включениям з точки зору кількості виконуваних ДІЙ.

21. Якою є оцінка ефективності роботи алгоритмів, що реалізують методи прямого сортування? ОбГрунтуйте свою відповідь.

Завдання

1. Реалізувати у вигляді програми алгоритм сортування за­дано! послідовності за зростанням методом прямого вибору.

2. Реалізувати у вигляді програми алгоритм сортування за­дано! послідовності за зростанням методом прямого обміну.

3. Реалізувати у вигляді програми алгоритм сортування за­дано! послідовності за зростанням методом прямого включен­ия.

4. Змінити алгоритми у завданнях 1-3 так, щоб сортування відбувалося за спаданиям.

5. Протестувати реалізовані у завданнях 1-4 алгоритми для масиву 15, 4, 10, 8, 6, 9, 16, 1, 7, 3, 11, 14, 2, 5, 12, 13.

6. Проаналізувати покрокове виконання завдання 5 щодо кількості виконуваних дій.

7. Підібрати власні тести, які доводить переваги й показу-ють недоліки кожного з методів прямого сортування для п > 100.

8. Зробити письмовий аналіз завдань 5-7.

157

ПОКРАЩЕНІ МЕТОДИ СОРТУВАННЯ

Сортування з двійковим включениям

Ефективність роботи розглянутого вище методу прямого включения залежить від:

• кількості порівнянь, які необхідно зробити протягом вико-нання алгоритму для визначення місцезнаходження елемента a_t у підпослідовності a_t, а₂, ..., a,_,;

• кількості зсувів, які необхідно виконати для вставления елемента а, на свое місце у підпослідовність а_х,а₂,...,а_і__ї.

Оскільки за умовою алгоритму a_t, a₂,..., a_t_ _t є вже впорядко-ваною частиною послідовності, то для знаходження в ній міс-цеположення елемента a_t можна використати бінарний пошук. Таке покращення називається методом з двійковим включен­иям (binary insertion).

3 урахуванням зазначеної модифікаці'ї алгоритму текст фрагмента програми, що реалізує алгоритм сортування за до-помогою включения, тепер буде таким:

for І := 2 to n do begin

x:=a[i]; L:=1;R:=i; while L<R do begin

m:=(L+R)div2; if a[m] <=x then L := m + 1 elseR :=m; end; for j := i downto R + 1 do

a[j]:=a[j-1]; a[R]:=x end;