Пошук у мережі

Мережею будемо називати множину вершин Р і множину дуг R, що їх з'єднують, та функцію d, яка задана на R у мно­жит дійсних чисел. Можна сказати, що d задає залежність між окремими вершинами, визначеними на дугах.

Далі мережу будемо визначати так:

S = (P,R,d).

Інколи d(x, у) інтерпретують як довжину дуги (х, у) Є R.

Для кращого розуміння поняття мережі та з'ясування, чому ми її розглядаємо в темі «Пошукові алгоритми», наведемо ти-пові приклади існування інформації, яку можна представити у вигляді мережі.

Наприклад, це може бути задача про взаємини щодо визна-чення обсягу постачання сировини в мережі, яку утворюють N підприємств одного відомства. А саме, на яку загальну суму підприємство х отримує сировину від інших підприємств, якщо відома інформація про постачання сировини підприєм-ства х, деякому підприємству у. на суму d.. (1 < і, j < N).

Ще одна подібна задача про банки. Нехай відома інформація про те, яку грошову суму винен кожний із банків іншим. Треба визначити, яку суму винен деякий банк х іншим банкам і яким саме, а також яку суму винні йому інші банки та які саме.

Отже, перейдемо до суті задачі в термінах мережі. Розгляне-мо приклад деякої мережі, яка мае т вершин (т = 9) і п дуг (п " 15), що з'єднують ці вершини (мал. 52).

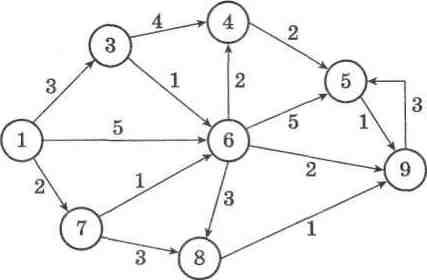
Мал. 52

Сформулюємо дві задачі, які найчастіше доводиться роз-в'язувати у зв'язку з мережею:

1) для фіксованої вершини х Є Р визначити всі дуги мережі вигляду (х, у) (виходи з х);

143

2) для фіксованої вершини хЄР визначити всі дуги мережі вигляду (у, х) (входи в х).

Будемо говорити про багатократний пошук необхідної ін-формації в мережі, стан якої не змінюється протягом ви конин-ня алгоритму.

Найпростіше, але найменш ефективно, застосовувати в кож­ному з випадків лінійний пошук. Але існують і ефективніші методи. Розглянемо деякі з них і визначимо, чому вони мають безпосереднє відношевня до скінченних автоматів.

Пред ставимо мережу S у вигляді таблиці, де окремі рядки є записами про конкретні дуги (табл. 14).

Таблиця 14

№ дуги	Вершина х	Вершина у	Вага d
1	7	8	3
2	3	4	4
3	5	9	1
4	9	5	3
5	4	5	2
6	8	9	1
7	3	6	1
8	7	6	1
9	1	3	3
10	1	7	2
11	6	4	2
12	1	6	5
13	6	8	3
14	6	5	5
15	6	9	2

Розглянемо спочатку задачу 1). Відомо, що для найшвид-шого пошуку краще мати справу з упорядкованою інфор-мацією. Тож надалі вважатимемо, що інформація в масиві S упорядкована за ключей х. Тепер пошук потрібної дуги х наба-гато спрощується, оскільки для цього можна застосувати бі-нарний пошук.

Однак цей пошук можна ще вдосконалити. Створимо допо-міжний одновимірний масив А з кількістю елементів, що дорів-нює кількості вершин мережі m. Елементами цього масиву А[х] будуть номери першого розміщення всіх дуг (х, у), що виходять із вершини х, у масиві S (мал. 53).

144

x = G				N	X	!/	d
				1	1	3	3
X	А(х)			2	1	7	2
1	1			3	1	6	5
2	0			4	3	4	4
3	4			5	3	6	1
4	6			6	4	5	2
5	7			7	5	9	1
6	8			8	6	4	2
7	12			9	6	8	3
8	14			10	6	5	5
9	15			11	6	9	2
				12	7	8	3
				13	7	6	1
				14	8	9	1
				15	9	5	3

Мал. 53

Побудувати масив А можна за допомогою такого алгоритму:

1) перше входження значения i вершини х у масив S занесе- мо вА[і];

2) поки не завершено перегляд масиву S, перейдемо до п. 1. Реалізація запропонованого алгоритму у вигляді тексту

Pascal-програми може виглядати так:

for j := 1 to m do

a[j]:=0; i:=1;

while i <= n do begin

k := s[i].x a[k] := i;

while (i <= n) and (s[i].x = k) do inc (i); end;

A тепер оцінимо побудований масив A. Оскільки він містить інформацію про перше входження кожної вершини х у впо-рядкований масив дуг S, що описуе всю мережу, то можна гово-рити про те, що він і є функцією переходів для всіх вершин X. А це є неодмінним атрибутом скінченного автомата і дає мож-ливість швидкого пошуку потрібної інформації.

На малюнку 53 показано, як можна здійснити пошук усіх дуг із вершини х -= 6 за допомогою масиву А. Інформація про по-

145

чаток розміщення в масиві А групи всіх дуг, що виходять із вершини х, міститься в елементі А[х]. Діалог про визначення всіх дуг, які виходять із вершини х, можна організувати за до-помогою такого фрагмента тексту Pascal-програми:

write ('Задайте номер вихідної вершини х:'); readln (к); i:=a[k]; if а[к] = О then

writeln ('У такої вершини вихідні дуги відсутні') else

repeat

writeln ('x = ', s[i].x, 'y= ', s[i].y, ' d = ', s[i].d); inc(i) until(s[i].xok)or(i = n);

Аналогічно можна розв'язати i задачу 2). Але, відсортував-ши масив S по у, втратимо можливість ефективно розв'язувати задачу 1).

Запропонуємо інший вихід. Створимо два допоміжні маси-ви: В[у] і С[у] (мал. 54).

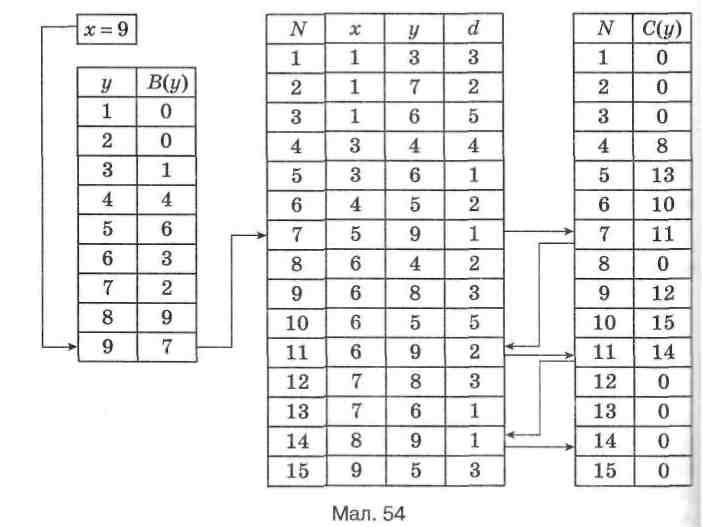
Масив В[у] (1 < у < т) буде побудований так само, як і ма­сив А[х]. Кожний елемент х у масиві В є першим входженнях

146

дуги (у, х) у масив S. Реалізація алгоритму його побудови може виглядати так:

forj := 1 torn do

b[j]:=0; for i := 1 to n do

if b[s[i].y] = 0

then b[s[i].yl :=i;

Масив С побудований інакше. Кількість його елементів збі-гається з кількістю дуг у мережі п. Його елементи вказують на послідовність читання дуг (у, х) у масиві S, що відповідає зрос-танню по у (мал. 54). Можна сказати, що масив С побудований за тим самим принципом, що й таблиця FAT у системній облас-ті дискового простору будь-якого зовнішнього носія комп'юте-ра: значения кожного елемента масиву С збігається з порядко-вим номером масиву S, де в полі у міститься наступив значен­ия, що збігається з шуканим.

Іншими словами, згідно з малюнком 54 масив С(у) ство-рюеться так: кожей його елемент вказуе на наступний номер рядка в S, де знаходиться така сама дуга (у, і). Алгоритм побу­дови масиву С описаної структури мовою Pascal, що використо-вує масив В, буде таким:

for i := 1 to n do

с[і]:=0; for k := 1 to m do begin i:=b[k]; if b[k] <> 0 then

while i <= n do begin j:=i; repeat | inc(i);

until (s[i].y = k) or (i > n); if i <= n then c[j] := i; end; end;

При такій організації масивів В(у) і С(у) проблема пошуку всіх входів у х зводиться до вибору адреси В(у), а потім послі-довних адрес з С(у):

write ('Задайте номер вхідної вершини у:'); readln (k); i:=b[k]; if c[i] = 0 then

147

writeln ('У такої вершини вхідні дуги відсутні') else begin repeat

writeln ('y = ', s[i].y,' x = ', s[i].x,' d = ', s[i].d); i:=c[i]; until (i > n) or (c[i] = 0); writeln ('y = ', s[i].y,' x = ', s[i].x,' d = ', s[i].d); end;

Допоміжні масиви В, С (так само як і А) є функціями перехо­ду для визначення станів під час пошуку всіх дуг, які виходять із задано!' вершини у. Тому ще раз підкреслимо, що наведений алгоритм пошуку в мережі можна віднести до класу скінчен-них автоматів.

Масиви А, В, С ще називають довідниками, а їх сукупність -довідкою для S.

Оцінювати цей метод треба окремо для пошуку виходів з х та для пошуку входов у х. Оскільки сортування вхідного масиву S та побудова масивів А, В і С виконується для заданої мережі ли­ше один раз, то для визначення оцінки ефективності пошуково-го алгоритму час, необхідний для цього, враховувати не будемо.

Пошук виходів для задано! вершини х не залежить від кіль-кості вершин самої мережі т, оскільки адреса її першого входу у масив S визначається як а[х]. Далі відбувається пошук за ви-значеною адресою в масиві S довжиною п. Тому оцінка цієїчас-тини пошукового алгоритму буде О(л).

Пошук входів для задано! вершини х також здійснюється в масиві перших входів усіх вершин у поле у масиву S аналогіч-но, як і для виходів: b[y]. А далі відбувається адресний пошук ycix інших входів у х за допомогою масиву С, довжина якого становить п елементів. Тому оцінка і цієї частини попгукового алгоритму буде також О(п).

/ Запитання для самоконтролю

1. Що називається мережею?

1. Наведіть приклади задач, які можна представити як пошук у ме­режи

2. Зобразіть приклади, наведені у пункті 2, у вигляді схем.

3. Зобразіть приклади, наведені у пункті 2, у вигляді таблиць.

4. Які дві задачі найчастішє пов'язують із мережею?

5. Яке призначення масиву А(х)?

2. Чому побудову масиву А(х) можна назвати побудовою функції переходу?

6. Опишггь алгоритм побудови масиву А(х).

3. Наведіть текст Pascal-програми, що відповідає алгоритму побу­дови масиву А(х).

148

10. Як здійснюється пошук потрібної інформації за допомогою ма­сиву А(х)?

11. Зобразіть схематично пошук потрібної інформації за допомогою масиву А(х).

12. Яке призначення масивів В(у) і С(у)?

13. Чому побудову масивів В(у) і С(у) можна назвати побудовою функцій переходу?

14. Опишіть алгоритм побудови масиву В(у).

15. Наведіть текст Pascal-програми, що відповідає алгоритму побу­дови масиву В(у).

16. Опишіть алгоритм побудови масиву С(у).

17. Наведіть текст Pascal-програми, що відповідає алгоритму побу­дови масиву С(у).

18. Як здійснюється пошук потрібної інформації за допомогою ма-сивів В{у) І С{у)?

19. Зобразіть схематично пошук потрібноі інформації за допомогою масивів В(у) І С(у).

20. Якою є оцінка ефективності роботи алгоритму пошуку в мережі?

Завдання

1. Розробити діалогову меню-орієнтовану програму роботи алгоритму пошуку в мережі, що є прикладом скінченного ав­томата.

2. Протестувати програму, складену згідно із завданням 1, для вершини, значения якої присутнє в полі х масиву S.

3. Протестувати програму, складену згідно із завданням 1, для вершини, значения якої відсутнє в полі х масиву S.

4. Протестувати програму, складену згідно із завданням 1, для вершини, значения якої присутнє в полі у масиву S.

5. Протестувати програму, складену згідно із завданням 1, для вершини, значения якої відсутнє в полі у масиву S.

6. Довести за допомогою підрахунку кількості переглядів масиву S, що алгоритм пошуку мережі, реалізований у завдан-ні 1, є лінійним.

7. Зробити письмовий аналіз виконання завдань 2—6.

149

Розділ V

0110 I

1 I !10Л

МЕТОДИ СОРТУВАННЯ

0 0 1 1 О I 10 10

10 0 1 01 10 1110' D 00 0 110 1

■

О 00 10

OCHOBHI ПОНЯТТЯ МЕТ0Д1В СОРТУВАННЯ

Класичним формулюванням задачі сортування (упорядку-вання) масиву є таке.

Нехай задано деякий масив значеиь а,, а₂, ..., а_л. Його необ-хідно перетворити так, щоб виконувалося співвідношення:

Аналогічною є і задача сортування заданого масиву за спа­даниям.

Одним з основних питань сортування елементів масивів є економія пам'яті, тобто переставлення елементів у масиві в межах самого масиву.

Є декілька класифікацій методів сортування. Перша з них -це за методикою сортування. Друга - за кількістю виконува-них операцій при виконанні самих алгоритмів.

За першою ознакою методи сортування поділяються на:

• сортування за допомогою вибору (by selection);

• сортування за допомогою обмінів (by exchange);

• сортування за допомогою включения (by insersion).

За другою ознакою всі методи сортування можна поділити на:

• прямі;

• покращені;

• удосконалені Надалі будемо розглядати методи сортування у такій послі-

довності: прямі, покращені, удосконалені. А в кожному з цих підрозділів будемо наводити методп, які відносяться до ме-тодів сортування за допомогою включения, вибору й обміну відповідно.