Входные и взаимные проводимости ветвей. Входное сопротивление. Теорема взаимности

На рис. 1.25 резисторы цепи не показаны. Рассмотрим две ветви: m и k. Пусть в ветви m находится ЭДС E_m (других ЭДС в схеме нет). ЭДС E_m вызовет токи в ветвях I_m = E_m·g_mm и I_k = E_m·g_km.

Коэффициенты g_mm и g_km являются, соответственно, входной и взаимной проводимостями. Величина R_вхm = 1/g_mm = E_m/I_m называется входным сопротивлением.

Теорема взаимности формулируется следующим образом: для любой линейной цепи ток в k-ветви, вызванный ЭДС E_m, находящейся в m-ветви (I_k=E_m·g_km), будет равен току I_m в m-ветви, вызванному ЭДС E_k (численно равной ЭДС E_m), находящейся в k-ветви (I_m=E_k·g_mk).

Доказательство: пусть ветви m и k являются ветвями связи, тогда по формуле из МКТ для первого случая I _k=E_mA_mk/, а для второго случая I_m=E_kA_km/. Поскольку  симметричен относительно главной диагонали, то A_mk = A_km. Следовательно, I_m = I_k, что и требовалось доказать. Наблюдается равенство проводимостей g_km = g_mk.

Для нелинейных цепей теорема взаимности неверна. Такие цепи называют необратимыми.

Линейные соотношения в электрических цепях

Если в линейной электрической цепи изменяется ЭДС или сопротивление в какой-либо одной ветви, то две любые величины (токи и напряжения) двух любых ветвей связаны друг с другом линейными зависимостями вида y = a + b·x. x – ток или напряжение первой рассматриваемой ветви и y – ток или напряжение второй рассматриваемой ветви.

Доказательство. Согласно принципу наложения формула для тока k-ветви может быть записана в форме: I_k=E₁·g_k1+E₂·g_k2+…+E_k·g_kk+…+ E_n·g_kn. Если в цепи только одна величина изменяется, например E_m, то все слагаемые, кроме слагаемого E_m·g_km, постоянны и могут быть заменены некоторым слагаемым A_k. Следовательно, I_k = A_k + E_m·g_km. Аналогично для p-ветви I_p = A_p+ E_m·g_pm.

Далее E_m = (I_p – A_p)/g_pm. И, наконец, I_k = a_k+ b_k·I_p,

где a_k = A_k – A_p g_km/g_pm; b_k = g_km/g_pm.

Коэффициенты a_k и b_k могут быть как положительны, так и отрицательны.

Так как любое сопротивление может быть заменено ЭДС (теорема компенсации, рассмотрена ниже), линейное соотношение между двумя величинами справедливо и при изменении резистивного сопротивления.

Теорема Гельмгольца-Тевенена (об активном двухполюснике). Метод эквивалентного генератора (МЭГ) (задачи 1.42-1.47 /5/)

Т еорема. Если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС Е_экв, равной напряжению на зажимах разомкнутой ветви, и с сопротивлением R_экв, равным входному сопротивлению активной цепи относительно разомкнутых зажимов, то ток в присоединённой ветви не изменится.

Доказательство теоремы выполним на основе метода наложения (рис. 1.26).

В качестве эквивалентного источника может быть использован и источник тока. При этом J_экв = Е_экв/R_экв; R_Jэкв = R_Еэкв.

Таким образом, чтобы этой теоремой воспользоваться, нужно найти параметры E_экв и R_экв двухполюсника. Их можно найти экспериментально, поставив опыты холостого хода и короткого замыкания (показано на рис. 1.27).

Метод эквивалентного генератора используется для определения тока в отдельной ветви сложной цепи. Порядок расчёта:

1. Определение ЭДС эквивалентного генератора. Для этого:

- в исследуемой ветви принимается положительное направление тока, ветвь размыкается и по току вводится напряжение U_хх;

- для простейшего контура с участием U_хх по второму закону Кирхгофа составляется уравнение, при этом токи снабжают индексом _х: I_qх;

- при разомкнутой ветви любым методом находят токи, вошедшие в уравнение;

- подставив их в уравнение, получают U_хх = Е_экв.

2. Отыскание сопротивление эквивалентного генератора R_экв. Для этого:

- в оставшейся части цепи исключают источники, заменяя их внутренними сопротивлениями R_E = 0, R_J = ;

- в случае необходимости преобразовывают схему и записывают её входное сопротивление относительно разомкнутой ветви: R_вх = R_экв.

3. Искомый ток находят по закону Ома: I = .

Преобразования электрических цепей (задачи 1.35-1.41 /5/)

Само по себе преобразование электрических цепей не является методом расчёта. Но оно способствует упрощению расчёта цепи. Естественно, что любое преобразование должно быть эквивалентным, то есть если заменяется какой-то участок цепи, то это не должно сказаться на токах и напряжениях на других участках.

Сюда относятся:

- замена последовательного, параллельного и смешанного соединения сопротивлений одним эквивалентным;

- замена реального источника тока эквивалентным источником ЭДС и наоборот;

- замена участка сложной цепи, имеющего два узла, эквивалентной ветвью на основе метода двух узлов;

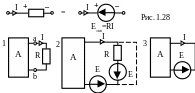
- замена сопротивления с известным током зависимым источником ЭДС (теорема о компенсации) (рис. 1.28);

- замена треугольника сопротивлений эквивалентной звездой и наоборот, а также другие преобразования.