1. Комплекс санның алгебралық түрі, қолданылатын амалдар мен қасиеттері. Жазықтықта кескіндеу және тригонометриялық түрі. Муавр формуласы. Комплекс саннан n-дәрежелі түбір табу формуласы.

Комплекс сандар алгебралық теңдеулерді шешу негізінде пайда болды.

Комплекс сан деп z=a+bi түріндегі санды айтамыз, мұндағы a және b –нақты сандар, ал i –жорамал бірлік, i²=–1. a комплекс санның нақты бөлігі, b –оның жорамал бөлігі. Re(z)= a, Im(z) = b

- комплекс сандар жиыны. Әрбір нақты сандар комплекс сан деп қабылдауға болады, себебі, үшін .

Комплекс сандар жиыны нақты сандар жиынының кеңеюі .

z=a+bi және =a–bi өзара түйіндес сандар деп аталады.

z₁=a+bi және z₂=c+di cандары тең

Комплекс сандарының қосындысы комплекс сан болады.

Қосудың қасиеттері:

"z₁,z₂,z₃C үшін (z₁+z₂)+z₃=z₁+(z₂+z₃),

$0C, "zC , z+0=0+z=z ,

"zC, $ –zC, z+(–z)=(–z)+z=0 ,

"z₁,z₂C; z₁+z₂=z₂+z₁ .

Комплек сандардың көбейтіндісі комплекс сан.

z=z₁×z₂=(a+bi)×(c+di)=(ac–bd)+(bc+ad)i.

Көбейтудің қасиеттері:

"z₁,z₂,z₃C (z₁×z₂)×z₃=z₁×(z₂×z₃) (ассоциативті),

$1C, "zC, z×1=1×z=z (1=1+0×i),

"zC, $ z^-1C, z×z^-1=z^-1×z=1 (z=a+bi және z^-1= 1/z=(a/(a²+b²))+((–b)/(a²+b²))i),

"z₁,z₂C, z₁×z₂=z₂×z₁ (коммутативті).

Қосу мен көбейту амалдары дистрибутивтілік заңымен байланысқан

.

Комплекс сандардың бөліндісі комплекс сан,

Комплекс сандардың геометриялық мағынасы және тригонометриялық түрі.

К омплекс сандарды координат жазықтығының көмегімен жазықтықтың нүктелері ретінде өрнектеуге болады. Ox - осінің бойына комплекс санның нақты бөлігін (a=a+0∙i), ал Oy осінің бойына оның жорамал бөлігін орналастырсақ (bi=0+bi) жазықтықта әрбір комплекс сан z(a,b) нүктесі түрінде анықталады. тік бұрышты

ïzï r=ïzï= .

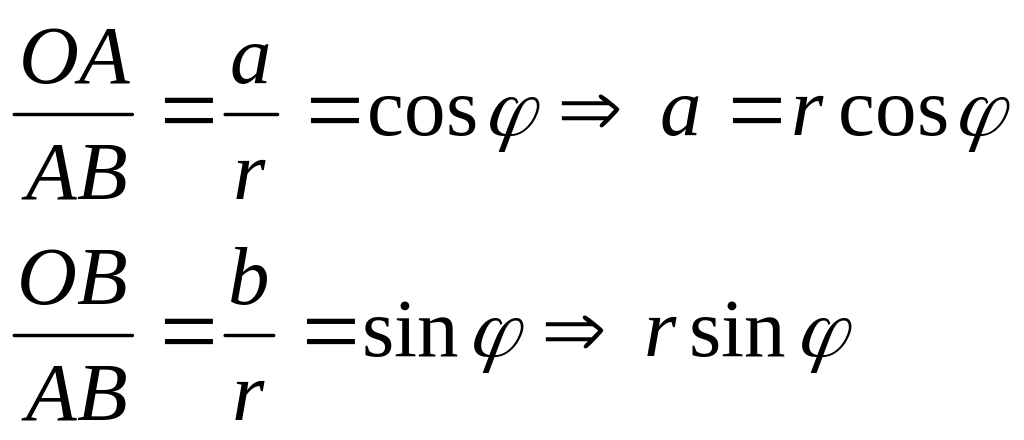
z=a+bi=r(cosφ+isinφ)- комплекс санның тригонометриялық түрі.

=r - комплекс санның модулі .

-комплекс санның аргументі.

Тригонометриялық түрдегі комплекс сандарға амалдар қолдану өте жеңіл.

Айталық,

z₁=r₁(cosφ₁+isinφ₁),

z₂=r₂(cosφ₂+isinφ₂) болсын.

Онда

Егер болса, онда

Муавр формуласы

Комплекс саннан n^ші дәрежелі түбір табу және 1 ден табылған түбірлердің тобы.

Айталық, а=r(cos +isin ) комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін

яғни комплекс санды дәрежелегенде оның модулі сол дәрежеге шығарылады, ал аргументі сол дәреже көрсеткішіне көбейтіледі.

теңдігін пайдаланып, Муавр формуласын бүтін теріс сандар үшін де пайдалануға болады. a=a+bi комплекс санын оң бүтін n дәрежеге шығару үшін Ньютонның биномын пайдаланған орынды, тек

ескерсек жеткілікті.

Муавр формуласының дербес түрін қарастырайық.

cos n

Теңдіктің оң жақ бөлігіне Ньютонның биномды формуласын қолданайық.

Мұндағы теңдігінің сол және оң жақ бөліктерін салыстырсақ,

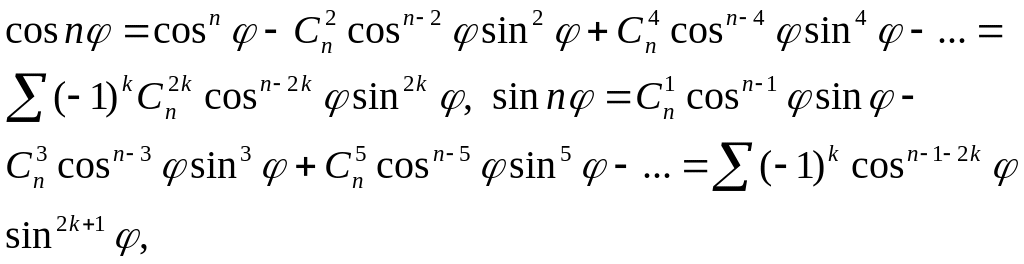
теңдіктерін аламыз.

Сонымен, , мұндағы

-ға әртүрлі мәндер беру арқылы түбірдің әртүрлі мәндерін аламыз.

Қорытынды. Комплекс сандардан n - ші дәрежелі түбірді әрқашан табуға болады және оның әртүрлі n мәні болады.