§ 6.8. Qo‘shaloq yulduzlar

Ko‘p holda osmondagi ikkita yulduz biri biriga yaqin joylashgan bo‘lib ko‘rinadi, aslida ularni juda katta masofalar ajratib turadi. Bunday tasodifiy juftliklar optik qo‘shaloq yulduzlar deb nomlanadi. Shunday bo‘lsada, ko‘pgina yaqin joylashgan yulduziy juftliklar bir xil masofada joylashgan bo‘lib, fizik juftlikni tashkil etadilar, bunda ikkala yulduz bir-birining atrofida aylanadilar. Barcha yulduzlarning deyarli yarimi Quyosh kabi yakka yulduzlardir, 50% dan ziyod yulduzlar ikkita va undan ko‘proq a’zolarga ega yulduzli sistemalarga taalluqlidir. Umumiy holda ko‘pchilik sistemalar ierarxik tuzilishga ega: uch karrali sistemalarda bitta yulduz qo‘shaloq yulduz atrofida, to‘rt karrali sistemalarda ikkita qo‘shaloq juftlik biri birining atrofida aylanadilar. Shunday qilib, ko‘p hollarda murakkab sistemalarni bir nechta pog‘onalarga ega juftliklar deb ko‘rsatish mumkin.

Qo‘shaloq yulduzlar ularni kuzatish usuli asosida sinflashtiriladi. Vizual juftliklarni ikkita yakka komponenta deb qabul qilish mumkin, bunda yulduzlar orasidagi masofa 0,1 burchak sekunddan kichik bo‘lmog‘i lozim. Komponentalarning o‘zaro joylashuvi ko‘p yillar davomida o‘zgarib boradi, chunki ular o‘zlarining orbitalari bo‘ylab harakatlanadilar (6.11 rasm). Astrometrik qo‘shaloqlarda faqat bitta yulduz ko‘rinadi, ammo undagi xususiy harakatining o‘zgaruvchanligi ko‘zga ko‘rinmas ikkinchi komponenta mavjudligidan dalolat beradi. Spektroskopik ko‘shaloq yulduzlar ularning spektrlari asosida topiladi. Bunda spektral chiziqlarning ikkita to‘plami yoki ana shu chiziqlar orasida davriy ravishda dopplercha siljish kuzatiladi, bu ham ko‘rinmas yo‘ldoshga ishora qiladi. Qo‘shaloqlarning to‘rtinchi sinfi fotometrik qo‘shaloq yoki tutuluvchan o‘zgaruvchan yulduzlardir. Bu sistemalarda juftlikning komponentalari muntazam biri-birini to‘sib o‘tadilar, oqibatda ularning umumiy yulduziy kattaliklari o‘zgarib turadi.

Qo‘shaloq yulduzlar, shuningdek, o‘zaro ta’sirlashuvlariga binoan ham sinflashtirilishlari mumkin. Keng juftliklarning komponentalari orasidagi masofa bir necha o‘n va bir necha yuz astronomik birliklar bo‘lib, ularning orbital davrlari bir necha o‘n yildan bir necha ming yilgacha tashkil etishi mumkin. Tig‘iz qo‘shaloq sistemalarda yulduzlar orasidagi masofa bir astronomik birlikdan yulduz radiusigacha teng bo‘lishi mumkin. Ularda orbital davr bir necha soatdan bir necha yilgacha bo‘ladi. Kontaktli qo‘shaloqlarda komponentalari shunchalik yaqinki, ular biri-biriga tegib turadi.

Qo‘shaloq sistemalardagi yulduzlar sistemaning massalar markazi atrofida harakatlanish orbitasi ham ellips ekanligi isbotlangan, va kuzatuvlarni sharhlaganda ko‘pincha komponentalarning biri qo‘zg‘almas, ikkinchisi esa, uning atrofida aylanadi deb olinadi.

6.11 rasm. Uzoq kuzatuvlar mobaynida vizual qo‘shaloqlarni kuzatib, komponentalari biri biriga nisbatan vaziyatlarini o‘zgartirishlarini payqash mumkin. Kryuger 60 yulduzining tasviri. ( Yerks observatoriyasi)

6.12 rasm. 1830 yilda ilk bor ξ Katta Ayiq qo‘shaloq yulduzining orbitasi kuzatuvlardan aniqlangan.

Vizual qo‘shaloqlar. Vizual qo‘shaloqni olib ko‘raylik, bunda bosh komponenta qo‘zg‘almas, yo‘ldoshi esa, orbita bo‘ylab uning atrofida harakatlanayapti deb faraz qilaylik. Yulduzlar orasidagi burchak masofani va pozitsion burchakni bevosita kuzatuvlardan aniqlash mumkin. Ko‘pyillik muntazam kuzatuvlardan foydalangan holda yo‘ldoshning relyativistik orbitasi topiladi. 6.12 rasmda 1830 yildagi ξ Katta Ayiq yulduzi misolida qo‘shaloqning dastlabki orbitasi ko‘rinishi tasvirlangan.

Vizual qo‘shaloq yulduzlarning kuzatuvlari fazo tekisligidagi nisbiy orbital ellipsning proeksiyasini beradi, bunda haqiqiy orbitaning vaziyati va shakli aniqlanmaydi. Shunday bo‘lsada, bosh yulduz nisbiy orbitaning fokal nuqtasida joylashishi lozim degan taxmindan ularni hisoblab topish mumkin. Bosh yulduzning proeksiyalangan nisbiy orbitadagi hisoblangan vaziyatidan chetlashishlari haqiqiy orbitaning batafsil orientatsiyasini topishga imkon beradi.

6.13 rasm. Qo‘shaloq sistemaning komponentalari umumiy massalar markazi atrofida harakatlanadilar. A1 va A2 berilgan vaqt momenti A da, mos ravishda, B va C uchun yulduzlarning vaziyatlarini belgilaydi

Orbitaning absolyut o‘lchamini qo‘shaloqlar orasidagi masofani bilgan holda aniqlash mumkin. Bular orqali Kepler qonunlaridan foydalanib, sistemaning umumiy massasi hisoblab topiladi.

Komponentalarning aloxida massalarini ikkala komponentalari massalar markazi atrofida harakatini kuzatishlaridan aniqlasa bo‘ladi. Bosh va yo‘ldosh yulduzlar orbita ellipslari katta yarimo‘qlari a₁ va a₂ bo‘lsin. Bundan, massalar markazigacha masofalariga muvofiq:

(6.43)

bo‘ladi, bunda m₁ va m₂ – massalarning tashkil etuvchilaridir. Nisbiy orbitaning katta yarimo‘qi

. (6.44)

Masalan, ξ Katta Ayiq yulduzi komponetalarining massalari 1,3 va 1,0 Quyosh massalariga tengligi aniqlangan.

Astrometrik qo‘shaloq yulduzlar. Astrometrik qo‘shaloqlarda massalar markazi atrofida faqat yorqin tashkil etuvchisining orbitasini kuzatish mumkin. Agar ko‘rinayotgan komponentaning massasi biror yo‘sinda, masalan, uning yorituvchanligidan aniqlansa, ko‘rinmas yo‘ldoshning ham massasini aniqlasa bo‘ladi.

1830 yilda ilk bor topilgan astrometrik qo‘shaloq yulduz Sirius edi, uning xususiy harakati o‘ziga xos to‘lqinsimon ko‘rinishga ega. Uning atrofida kichik yo‘ldosh mavjud deb taxmin qilindi, u bir necha o‘n yildan so‘ng topildi (6.11 va 6.14 rasmlar). Ushbu qo‘shaloqning yo‘ldoshi Sirius B umuman yangi turdagi obyekt, ya’ni, oq karlik bo‘lib chiqdi.

6.14 rasm. Sirius va uning yo‘ldoshining fazodagi harakat yo‘llari

Sayyoraviy sistemalarni axtarish maqsadida Quyoshga yaqin tevaragida joylashgan yulduzlarning xususiy harakatlari batafsil o‘rganib chiqildi.

Masalan, harakatlarini o‘rganish orqali Barnard yulduzi ko‘rinmas yo‘ldoshlarga ega deb gumon qilinsada, boshqa yulduzlar atrofida sayyoraviy sistemalar topilganicha yo‘q, ular spektroskopik kuzatuvlar orqali ham tadqiq qilindi.

Spektroskopik qo‘shaloqlaryu Spektroskopik qo‘shaloq yulduzlar (6.15 rasm) xatto eng kuchli teleskoplarda ham kuzatilganda yakka yulduzlardek ko‘rinadilar, ammo ularning spektrlari muntazam davriy o‘zgarishlarga egadir. Dastlabki spektral qo‘shaloq 1880 yilda topilgandi, unda ζ UMa yoki Mitsar yulduzining spektral chiziqlari teng vaqtlar oralig‘ida ikkitaga parchalanib turishi aniqlandi.

Spektral chiziqdagi Doplercha siljish radial tezligiga to‘g‘ri proporsional. Shunday qilib, spektral chiziqlarning eng kuchli ajralishi komponentalardan biri kuzatuvchiga yaqinlashayotganga, ikkinchisi esa, uzoqlashayotganga mos keladi.

Spektral chiziqlardagi o‘zgarish davri yulduzlarning orbital davrining o‘zginasidir. Afsuski, orbitaning fazodagi vaziyatini aniqlaydigan umumiy usuli yo‘q. Kuzatilayotgan tezlik v haqiqiy tezlik v₀ bilan

v = v₀ sin i (6.45)

munosabatda bog‘langan, bu erda i – ko‘rish nuri bilan orbita tekisligi orasidagi burchak.

6.15 rasm. Spektral qo‘shaloq k Ari yulduzining spektri. Yuqoridagi spektrda spektral chiziqlar yakka-yakka, quyidagisida ikkilangan. (Lik observatoriyasi).

Komponentalari massalar markazi atrofida doiraviy orbita bo‘ylab harakatlanayotgan qo‘shaloqni olib ko‘raylik. Orbita radiuslari a₁ va a₂ bo‘lsin. Massalar markazi ta’rifidan m₁a₁ = m₂a₂, bunda a = a₁ + a₂ deb yozamiz va undan

. (6.46)

kelib chiqadi. Haqiqiy orbital tezligi

,

bu erda P – orbital davrdir. (9.3) ga binoan kuzatilayotgan orbital tezlik

bo‘ladi. (6.47)

Bunga (9.4) ni olib qo‘yamiz va

ni qo‘lga kiritamiz. Keplerning uchinchi qonunidan foydalanib, massalar funksiyasi tenglamasini olamiz:

. (6.48)

Agar spektroskopik qo‘shaloqda komponentalaridan biri spektral chiziqlari kuzatilmaydigan darajada zaif bo‘lsa, faqat P va v₁ topiladi. Unda (6.48) tenglamada massalar funksiyasi sifatida faqat chap tomondagi xad qoladi. U holda komponentalarining massalari hamda umumiy massa aniqlanmaydi. Agar ikkala komponentalarning spektral chiziqlari kuzatilsa, v₂ ham aniq bo‘ladi. Unda (6.47) dan quyidagi topiladi: , undan tashqari, massalar markazi aniqlanishi 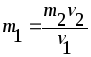ni beradi.

Uni (6.48) ga olib qo‘yib, mos ravishda m₂ sin³i hamda m₁ sin³i lari aniqlanishi mumkin. Bunda orbitaning qiyaligi ma’lum bo‘lsa ham, haqiqiy massalarini aniqlab bo‘lmaydi.

(6.47) dan qo‘shaloqning orbita o‘lchami yoki katta yarimo‘qi a topilishi mumkin, aniqligi esa, sini ning ko‘paytiruvchisiga bog‘liq bo‘ladi. Umumiy holda qo‘shaloq yulduzlarning orbitalari doiraviy emas, oqibatda yuqoridagi ifodalarini shu ko‘rinishlari bo‘yicha qo‘llab bo‘lmaydi. Ekssentrik orbitada ekssentrisiteti ortgan sari tezlikning shakli oddiy sinusoidadan shunchalik farqlanib boradi. Tezlikning o‘zgarish shaklidan ekssentrisitet hamda periastr uzunlamasi aniqlanishi mumkin. Ularni bilgan holda massalar funksiyasi yoki aloxida komponentalarning massalari sin³i ning ko‘paytiruvchisi aniqligi darajasida qayta topilishi mumkin.

Yaqin tevarakdagi yulduzlarning spektrlarini aniq tadqiqotlaridan o‘lchami sayyoralardek bo‘lgan bir nechta yo‘ldosh topildi. 1995 – 2002 yillarda massalari 0,1 dan 13 gacha Yupiter massalari oralig‘ida bo‘lgan yuztaga yaqin ekzosayyoralar kuzatildi.

Fotometrik qo‘shaloq yulduzlar. Fotometrik qo‘shaloqlarda umumiy yorqinlikning davriy o‘zgarishlari sistemadagi komponentalarining harakatlari tufayli kelib chiqadi. Odatda fotometrik juftliklar biri birini to‘sib o‘tadilar, bunda yorqinlikning o‘zgarishlari nafaqat tutilishlari tufayli, balki yaqin joylashgan komponentalari sirtlari ko‘tarilish-pasayish effektlari sababli shakllarining ellipsoidal ko‘rinishga egaligidan ham sodir etiladi. Bunday sistemalarda komponentalarning biri yoki ikkalasi ham ko‘tarilish-pasayish tufayli ellipsoidal shaklga kirgan bo‘ladi.

6.16 rasm. Algol, Liraning β va Katta Ayiqning W turidagi qo‘shaloq sistemalarning ravshanlik egri chiziqlari ko‘rinishlari. Taqqoslash uchun Quyoshning o‘lchami berilgan.

Orbitaning turli joylarida shakli buzilgan komponenta sirtining proeksiyalanadigan yuzasi o‘zgarib turadi. Sirtidagi harorati ham ko‘tarilgan do‘ngliklar qismida pastroq bo‘ladi. Ushbu faktorlar birgalikda yorqinliklarining kichik o‘zgarishlarini keltirib chiqaradi.

To‘siluvchan qo‘shaloqlarda orbita qiyaligi 90° ga yaqin bo‘lishi lozim. Faqat bunday spektroskopik juftliklarda qiyalik ma’lum bo‘lishi tufayli massalari aniqlanishi mumkin.

Tutuluvchan o‘zgaruvchan yulduzlarda yulduziy kattaliklari o‘zgarishi vaqt funksiyasi sifatida taqdim etilishi yorqinlik egri chizig‘i deb nomlanadi. Yorqinlikning egri chizig‘ining shakliga ko‘ra bunday yulduzlar uchta asosiy turga bo‘linadi, bular: Algol, Liraning β yulduzi va Katta Ayiqning W yulduzidir (9.6 rasm).

Algol yulduzlari. Algol turidagi tutuluvchan o‘zgaruvchan yulduzlar Perseyning β yoki Algol yulduzi kashf qilingandan so‘ng shunday deb nomlandilar. Davrning kattagina qismida ravshanlik egri chizig‘i deyarli o‘zgarmasdir. Bu esa, yulduzlar aloxida-alohida ko‘ringan fazalariga mos keladi, o‘sha momentlarda umumiy yulduziy kattalik o‘zgarmaydi. Ravshanlik egri chizig‘ida ikki xil minimum kuzatiladi, ulardan biri – bosh minimum ikkinchisiga nisbatan ancha chuqurroq. Ushbu effekt yulduzlar ravshanligidagi farqlaridan kelib chiqadi. Bosh yulduz, u odatda nisbatan sovuqroq gigantdir, kichikroq, ammo qaynoqroq komponentani to‘sib o‘tganda ravshanlik egri chizig‘ida chuqur minimum kuzatiladi. Kichik, ammo yorqinroq yulduz gigantning diskidan o‘tayotganda sistemaning umumiy yulduziy kattaligi unchalik kuchli o‘zgarmaydi.

Minimumlarning shakli tutilishlar to‘liq yoki qisman bo‘lishiga bog‘liqdir. Qisman tutilishlarda ravshanlik egri chizig‘i silliqroq, chunki yorqinlik tutilish chuqurligiga monand sekin-astalik bilan o‘zgaradi. To‘liq tutilishlarda komponenta butunlay ko‘rinmay qoladigan oraliq mavjud. Bu paytda umumiy yorqinlik deyarli o‘zgarmas, ravshanlik egri chizig‘idagi minimumida esa, yassi tub kuzatiladi.

Algol turidagi o‘zgaruvchanlarda minimumlarning shaklidan orbita qiyaligi haqida ham ma’lumot olish mumkin.

Minimumlarning davomiyligi yulduzlar radiuslari bilan orbita o‘lchamlari nisbatiga bog‘liqdir. Agar yulduz bir vaqtning o‘zida ham spektral qo‘shaloq bo‘lsa, orbitaning haqiqiy o‘lchamlarini topish mumkin. U holda sistemagacha masofani aniqlamasdan ham komponentalarning massalarini, orbita o‘lchamini, binobarin, yulduzlarning radiuslarini aniqlash mumkin.