
- •II semestr 223
- •So’z boshi
- •Fan dasturi
- •I. Ўқув фанининг долзарблиги ва олий касбий таълимдаги ўрни
- •II. Ўқув фаннинг мақсади ва вазифалари
- •III. Асосий назарий қисм (маъруза машғулотлари) Сферик астрономия асослари
- •Амалий астрономия масалалари
- •Осмон механикаси элементлари: сайёралар ҳаракати
- •Астрофизика тушунчалари ва телескоплар
- •Қуёш ва унинг тизими физикаси
- •Юлдузлар физикаси асослари
- •Галактика астрономияси
- •Космогония ва космология
- •IV. Амалий машғулотларни ташкил этиш бўйича кўрсатма ва тавсиялар
- •V. Лаборатория ишларини ташкил этиш бўйича кўрсатмалар
- •VI. Мустақил таълимни ташкил этишнинг шакли ва мазмуни
- •Фойдаланиладиган адабиётлар рўйҳати Асосий дарсликлар ва ўқув қўлланмалар
- •Қўшимча адабиётлар
- •Ishchi o’quv dasturi
- •Тошкент – 2017
- •1. Ўкув фанини ўқитилиши бўйича услубий кўрсатмалар
- •2. Маъруза машғулотлари Сферик астрономия асослари
- •Амалий астрономия масалалари
- •Осмон механикаси элементлари: сайёралар ҳаракати
- •Астрофизика тушунчалари ва телескоплар
- •Қуёш ва унинг тизими физикаси
- •Юлдузлар физикаси асослари
- •Галактика астрономияси
- •Космогония ва космология
- •3. Амалий машғулотлар
- •4. Лаборатория ишларини ташкил этиш бўйича кўрсатмалар
- •5. Мустақил таълимни ташкил этишнинг шакли ва мазмуни
- •Мустақил таълим мавзулари
- •6. Фойдаланиладиган адабиётлар рўйҳати Асосий дарсликлар ва ўқув қўлланмалар
- •Қўшимча адабиётлар
- •Интернет сайтлари
- •Талабалар билимини баҳолаш мезонлари
- •I semestr Ma’ruza materiallari
- •§ 1. Astronomiya fani: vazifalari va amaliy ahamiyati
- •§ 2. Astronomiyaning zamonaviy bo’limlari
- •I bob. Sferik astronomiya asoslari
- •§ 1.1. Samo jismlari va yulduz turkumlari
- •§ 1.2. Yoritgichlarning ko’rinma harakati
- •§ 1.3. Osmon sferasi va uning elementlari
- •§ 1.4. Gorizontal va ekvatorial koordinatalar sistemalari
- •§ 1.5. Kuzatuvchi kenglamasi turlari va olam qutbuning gorizontdan balandligi
- •§ 1.6. Yerning sutkalik aylanish oqibatlari
- •§ 1.7. Ekliptika va unga bog’liq koordinatalar sistemasi
- •§ 1.8. Vaqtni kuzatuvdan aniqlash usullari
- •§ 1.9. Vaqt o‘lchash tizimlari
- •§ 1.10. Taqvim va uning turlari
- •§ 1.11. Yulian kunlari va sana o‘zgarish chizig‘I
- •§ 1.12. Sferik uchburchak: sferik trigonometriyaning asosiy formulalari
- •§ 1.13. Parallaktik uchburchak. Koordinatalar sistemalariaro o‘tish formulalari
- •§ 1.14. Refraksiya
- •§ 1.15. Parallaks
- •§ 1.16. Presessiya va nutatsiya
- •§ 1.17. Yoritgichlarning chiqish va botish momentlarini aniqlash
- •II bob. Astronomiyaning amaliy va astrometrik masalalari
- •§ 2.1. Yer radiusini aniqlash. Triangulyasiya usuli
- •§ 2.2. Kuzatuvchining geografik uzunlama va kenglamasini topish
- •§ 2.3. Quyosh sistemasi jismlarigacha bo‘lgan masofalarni aniqlish
- •§ 2.4. Quyosh sistemasi jismlarining o‘lchamlarini aniqlish
- •§ 2.5. Oy fazalari va tutilishi
- •§ 2.6. Quyosh tutilishi. Saros
- •§ 2.7. Fundamental va fotografik astrometriya
- •§ 2.8. Yulduzlarning xususiy harakati
- •III bob. Osmon mexanikasiga kirish
- •§ 3.1. Olamning geliotsentrik sistemasi va osmon mexanikasi masalalari
- •§ 3.2. Sayyoralarning sirtmoqsimon ko‘rinma harakati
- •§ 3.3. Sayyoralar konfiguratsiyalari va aylanish davrlari
- •§ 3.4. Sayyoralar orbita elementlari
- •§ 3.5. Kepler va Nyuton qonunlari
- •§ 3.6. Keplerning umumlashgan 3-qonuni
- •§ 3.7. Uch jism masalasi va uning chegaralangan holi
- •§ 3.8. Ko‘tarilishlar va pasayishlar
- •§ 3.9. Quyosh sistemasining barqarorlik muammosi
- •IV bob. Astrofizika tushunchalari va teleskoplar
- •§ 4.1. Elektromagnit nurlanish spektri va uning astrofizik tadqiqoti
- •§ 4.2. Yoritgichlarning ko‘rinma va absolyut kattaliklari
- •§ 4.3. Nurlanish qonunlari
- •§ 4.4. Astrofizik obyektlar nurlanishining spektral tahlili
- •§ 4.5. Spektral chiziqlarning Dopler siljishi
- •§ 4.6. Spektral qurilmalar
- •§ 4.7. Astrofizik jismning temperaturasi turlari
- •§ 4.8. Astrofizik uskunalar va teleskoplar
- •§ 4.9. Optik teleskoplar va ularning asosiy ko‘rsatgichlari
- •§ 4.10. Radioteleskoplar
- •§ 4.11. Infraqizil astronomiya
- •Amaliy mashg’ulot materiallari
- •Uyga vazifa
- •Uyga vazifa
- •Dars davomida talabalarga beriladigan masalalar.
- •Uyga vazifa
- •Dars davomida talabalarga beriladigan masalalar.
- •Uyga vazifa
- •Laboratoriya mashg’ulot materiallari
- •Nazariy qism.
- •Umumiy ko’rsatmalar
- •Yulian sanani hisoblash
- •Nazariy qism.
- •II semestr Ma’ruza materiallari
- •§ 5.1. Quyoshning umumiy xarakteristikalari va ichki tuzilishi
- •§ 5.2. Quyoshning spektri, temperaturasi, tarkibi va yadrosi
- •§ 5.3. Fotosfera va uning aktiv sohalari
- •§ 5.4. Xromosfera va uning aktiv elementlari
- •§ 5.5. Quyosh toji va uning radionurlanishi
- •§ 5.6. Quyosh aktivligining davriy o‘zgarishi
- •§ 5.7. Yer tipidagi sayyoralar
- •§ 5.8. Gigant sayyoralar
- •§ 5.9. Asteroidlar va mitti sayyoralar
- •§ 5.10. Kometalar
- •§ 5.11. Meteorlar va meteoritlar
- •VI bob. Yulduzlar fizikasi asoslari
- •§ 6.1. Normal yulduzlar
- •§ 6.2. Yulduzlarning spektral sinflari
- •§ 6.3. Spektr-yorqinlik diagrammasi
- •§ 6.4. Yulduzlar massasi
- •§ 6.5. Yulduzlar o‘lchamlarini aniqlash
- •§ 6.6. Massa-yorqinlik-radius bog‘liqligi
- •§ 6.7. Yulduzlarning ichki tuzilishi
- •§ 6.8. Qo‘shaloq yulduzlar
- •§ 6.9. O‘zgaruvchan yulduzlar
- •§ 6.10. Yangi va o‘tayangi yulduzlar
- •§ 7.1. Somon Yo‘li Galaktikasi va uning ichki tuzilishi
- •§ 7.3. Quyosh sistemasining xarakati
- •§ 7.4. Yulduzlarning tarqoqsimon va sharsimon to‘dalari
- •§ 7.6. Spiral tarmoqlar
- •VIII-bob. Galaktikadan tashqi astronomiya
- •§ 8.1. Galaktikalarning Xabbl klassifikatsiyasi
- •§ 8.2. Galaktikalarning maxalliy guruxi
- •§ 8.3. Galaktikalargacha masofalarni aniqlash usullari
- •§ 8.4. Galaktikalar to’dalari
- •§ 8.5. Yadrosi aktiv galaktikalar
- •§ 8.6. Koinot modeli va tuzilishi
- •Amaliy mashg’ulot materiallari
- •Uyga vazifa
- •Laboratoriya mashg’ulot materiallari
- •Назарий қисм
- •Ҳисобот
- •§ 1. Юлдузларнинг массаларини аниқлаш
- •§ 2. Юлдузларнинг ўлчамларини аниқлаш
- •§ 3. Зичлик
- •Mustaqil ta’lim mashg’ulotlari
- •Мустақил таълим мавзулари
- •Glossariy
- •Ilovalar Tarqatma materiallar
- •Testlar Test savollari
§ 4.2. Yoritgichlarning ko‘rinma va absolyut kattaliklari
Eramizdan oldingi II asrda Gipparx ko‘z bilan ko‘rinadigan yulduzlarni ularning ko‘rinma ravshanligi bo‘yicha oltita sinfga bo‘lgan edi. Birinchi sinf eng ravshan yulduzlarni, oltinchisi esa qo‘rollanmagan ko‘z bilan ko‘rib bo‘ladigan eng hira yulduzlarni qamrab olgan.
Odam ko‘zi yorug‘lik nurining ravshanligini nochiziqli ravishda qabul qiladi. Agarda uchta yulduzning oqim zichliklari 1:10:100 nisbiy proporsiyasida bo‘lsa, unda birinchi va uchunchi yulduzlarning ravshanliklari ayirmasi ikkinchi va uchinchi yulduzlarning ravshanliklari ayirmasiga teng. Teng ravshanliklar nisbati ko‘rinma ravshanliklar ayirmasiga mos keladi: odam ravshanlikni logarifmik tarzda qabul qiladi.
Osmon jismlaridan kelayotgan nurlanish energiyasining miqdori, mazkur jism fizik tabiatini o‘rganishda eng muhim xarakteristik kattaliklardan hisoblanadi. Nurlanish energiyasining miqdori uning bevosita o‘lchash asbobiga etib kelgan miqdorini o‘lchash orqali yoki nurlanish qobiliyati ma’lum bo‘lgan boshqa nurlanuvchi jismning nurlanish energiyasining miqdori bilan solishtirish orqali aniqlanadi.
Yuza
elementi
 dan nurlanish o‘tyapdi deb faraz qilamiz (4.1-rasm). Nurlanishning
ayrim qismi
dan nurlanish o‘tyapdi deb faraz qilamiz (4.1-rasm). Nurlanishning
ayrim qismi
 dan
dan
 fazoviy burchak ostida chiqib ketadi;
fazoviy burchak ostida chiqib ketadi;
 va yuzaga normal orasidagi burchakni
va yuzaga normal orasidagi burchakni
 deb belgilayiz. Shunda
deb belgilayiz. Shunda
 vaqt davomidaushbu fazoviy berchakga chastotasi
vaqt davomidaushbu fazoviy berchakga chastotasi
 chastotalar intervalidagi nurlanishning energiya miqdori quyidagiga
teng:
chastotalar intervalidagi nurlanishning energiya miqdori quyidagiga
teng:

|
|
|
4.1
– rasm. Nurlanish intensivligi
|
 koeffitsienti –
koeffitsienti –
 fazvoiy burchak yo‘nalishida
fazvoiy burchak yo‘nalishida
 chastotali nurlanishning hususiy
intensivligi. Uni
o‘lchash birligi
chastotali nurlanishning hususiy
intensivligi. Uni
o‘lchash birligi
 ga teng.
ga teng.
Ko‘rib
turganimizdek, yuza elementi
 ning proeksiyasi
ning proeksiyasi
 va bu o‘z navbatida
va bu o‘z navbatida
 kerakligini ko‘rsatadi. Agarda intensivlik yo‘nalishga bog‘liq
bo‘lmasa, unda
kerakligini ko‘rsatadi. Agarda intensivlik yo‘nalishga bog‘liq
bo‘lmasa, unda
 energiyasi nurlanish yo‘nalishiga perpendekulyar bo‘lgan yuza
elementiga to‘g‘ri proporsional bo‘ladi.
energiyasi nurlanish yo‘nalishiga perpendekulyar bo‘lgan yuza
elementiga to‘g‘ri proporsional bo‘ladi.
Barcha
mumkin bo‘lgan chastotalarni o‘z ichiga qamram olgan intensivlik
umumiy
intensivlik
deyiladi va u
 ni chastotalar bo‘yicha integrallash orqali topiladi:
ni chastotalar bo‘yicha integrallash orqali topiladi:

Kuzatuvlar
nuqtai nazaridan muhimroq bo‘lgan kattaliklar bu energiya
oqmimi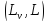 yoki qisqacha oqim
va oqim
zichligi
–
yoki qisqacha oqim
va oqim
zichligi
–
 .
Oqim zichligi yuza birligiga to‘g‘ri keladigan nurlanish
quvvatini beradi; shunda oqim zichligi aniq bir chastotadami yoki
umumiy oqim zichligi qaralayotgan holga bog‘liq holda uning
kattaligi
.
Oqim zichligi yuza birligiga to‘g‘ri keladigan nurlanish
quvvatini beradi; shunda oqim zichligi aniq bir chastotadami yoki
umumiy oqim zichligi qaralayotgan holga bog‘liq holda uning
kattaligi
 yoki
yoki
 bo‘lishi mumkin.
bo‘lishi mumkin.
Kuzatilayotgan
oqim zichligi odatda kichik bo‘ladi, shuning uchun
 kattaligi ancha katta va noqulay bo‘ladi. Shuning uchun, ayniqsa
radioastronomiyada, zichliq oqimi ko‘p hollarda yanskiyda
kattaligi ancha katta va noqulay bo‘ladi. Shuning uchun, ayniqsa
radioastronomiyada, zichliq oqimi ko‘p hollarda yanskiyda
 beriladi.
Bir yanskiy
beriladi.
Bir yanskiy
 teng.
teng.
Nurlanish manbasini kuzatayotganimizda biz aslida nur qabul qilgich tomonidan ma’lum vaqt davomida to‘plagan energiya miqdorini o‘lchaymiz va u nurlanish zichligining nurlanishni-to‘plash yuzasi hamda vaqt intervali bo‘yicha integraliga teng.
Nurlanish
zichligi
 berilgan
berilgan
 chastotada intensivlik birligida quyidagicha ifodalanishi mumkin:
chastotada intensivlik birligida quyidagicha ifodalanishi mumkin:

bu erda integrallash barcha imkon bo‘lgan yo‘nalishlar bo‘yicha olinadi. Shunga o‘hshash umumiy oqim zichligi ham topiladi:

Masalan,
agarda nurlanish izotrop
bo‘lsa, ya’ni agarda
 yo‘nalishga bog‘liq bo‘lmasa, unda quyidagiga ega bo‘lamiz:
yo‘nalishga bog‘liq bo‘lmasa, unda quyidagiga ega bo‘lamiz:

Fazoviy
burchakning elementi
 birlik sferadagi yuza elementiga teng. Sferik koordinatalarda
(4.2-rasm, hamda 5.A Ilovada):
birlik sferadagi yuza elementiga teng. Sferik koordinatalarda
(4.2-rasm, hamda 5.A Ilovada):

|
|
|
|
4.2
– rasm. Cheksiz kichik fazoviy burchak |
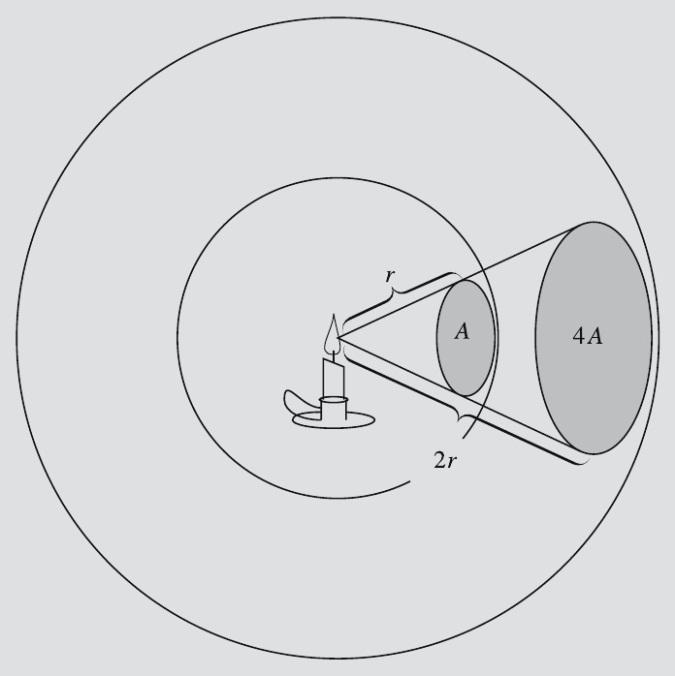
4.3
– rasm. Nuqtaviy manbadan |
Uni (4.3) ifodaga qo‘ysak, nurlanish oqimi yo‘qligini ko‘rishimiz mumkin:

Bu degani, qaralayotgan yuzaga kelib tushgan energiya miqdori undan chiqib ketgan energiya miqdoriga teng. Agarda biz yuzani kesib o‘tayotgan nurlanish miqdorini bilmoqchi bo‘lsak, unda, misol uchun, yuzadan chiqib ketayotgan nurlanishni topishimiz mumkin. Izotrop nurlanishi uchunbu

Astronomiyada tengishli adabiyotlarda intensivlik va yorqinlik kabi terminlarda bir qancha noaniqliklar bor. Oqim zichligi hali xech qaerda aynan oqim zichligi deyilmagan, balkim uning o‘rniga intensivlik yoki (omad chopsa) oqim deyilgan, xolos. Shuning uchun o‘quvchi har doim bu atamalarning ma’nosiga diqqat bilan e’tibor berib, nazorat qilishi kerak.
Oqim
biron bir yuzadan o‘tuvchi va
 larda
ifodalanadigan quvvatni anglatadi. Yulduzdan
larda
ifodalanadigan quvvatni anglatadi. Yulduzdan
 fazoviy burchak ostida chiqqan oqim
fazoviy burchak ostida chiqqan oqim
 ga teng,
ga teng,
 esa
esa
 masofada kuzatilgan oqim zichligi. Umumiy
oqim bu
manbani o‘rab turuvchi yopiq yuzadan o‘tuvchi oqimdir.
Astronomlar odatda yulduzning to‘liq oqimini yorqinlik
masofada kuzatilgan oqim zichligi. Umumiy
oqim bu
manbani o‘rab turuvchi yopiq yuzadan o‘tuvchi oqimdir.
Astronomlar odatda yulduzning to‘liq oqimini yorqinlik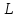 deb atashadi. Bu borada berilgan
deb atashadi. Bu borada berilgan
 chastotadagi
chastotadagi
 yorqinligi
haqida gapirishimiz mumkin
yorqinligi
haqida gapirishimiz mumkin
 .
(Buni fizikada qo‘llaniladigan yorug‘lik oqimi bilan
adashtirmaslik kerak, u ko‘z sezgirligini inobatga oladi).
.
(Buni fizikada qo‘llaniladigan yorug‘lik oqimi bilan
adashtirmaslik kerak, u ko‘z sezgirligini inobatga oladi).
Agarda
manba (masalan oddiy yulduz) izotrop ravishda nurlasa, unda uning
nurlanishi
 masofada yuzasi
masofada yuzasi
 ga teng bo‘lgan sferik yuza bo‘yicha bir tekis taqsimlanadi
(4.3-rasm). Agarda ushbu yuzadan o‘tuvchi nurlanishning oqim
zichiligi
ga teng bo‘lgan sferik yuza bo‘yicha bir tekis taqsimlanadi
(4.3-rasm). Agarda ushbu yuzadan o‘tuvchi nurlanishning oqim
zichiligi
 bo‘lsa, unda umumiy oqim:
bo‘lsa, unda umumiy oqim:

Agarda
biz nurlanish hosil bo‘lmaydigan va yo‘qolib ketmaydigan, manbaga
nisbatan tashqari fazoda bo‘lsak, unda yorqinlik masofaga bog‘liq
bo‘lmaydi. Nurlanio‘ zichiligi esa, boshqa tomondan,
 ga
proporsional ravishda kamayadi.
ga
proporsional ravishda kamayadi.
Qo‘lam
(cho‘zilgan) obyektlar (faqat nuqtaviy manba ko‘rinishida
kuzatiladigan yulduzlardan farqli) uchun sirtiyravshanlik
kattaligini kiritishimiz mumkin, bu birlik fazoviy burchakga to‘g‘ri
keladigan zichlik oqimidir (4.4-rasm). Endi kuzatuvchi fazoviy
burchakning uchida joylashgan deb faraz qilamiz. Sirtiy ravshanlik
masofaga bog‘liq emas, buni quyidagicha tushunishimiz mumkin.
 sohadan kelayotgan oqim zichligi masofa kvadratiga teskari
proporsionaldir. Ammo shu bilan birga
sohadan kelayotgan oqim zichligi masofa kvadratiga teskari
proporsionaldir. Ammo shu bilan birga
 sohaga
tayangan fazoviy burchak ham
sohaga
tayangan fazoviy burchak ham
 proporsional
proporsional
 .
Shunday
qilib, sirtiy ravshanlik
.
Shunday
qilib, sirtiy ravshanlik
 doimiy
(konstanta) bo‘lib qoladi.
doimiy
(konstanta) bo‘lib qoladi.
|
|
|
4.4
– rasm. Kuzatuvchi doimiy bo‘lagn
|
Nurlanishning
energiya
zichligi birlik
xajmga to‘g‘ri keladigan energiya miqdoridir
birlik
xajmga to‘g‘ri keladigan energiya miqdoridir
 :
:
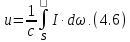
|
|
|
4.5
– rasm. |
 sirtga perpendekulyar ravishda
sirtga perpendekulyar ravishda
 fazoviy burchak ostida
fazoviy burchak ostida
 intensivlikga ega bo‘lgan nurlanish kelyapti (4.5-rasm).
intensivlikga ega bo‘lgan nurlanish kelyapti (4.5-rasm).
 vaqt
davomida nurlanish
vaqt
davomida nurlanish
 masofani
bosib o‘tadi va
masofani
bosib o‘tadi va
 xajmni
to‘ldiradi. Endi
xajmni
to‘ldiradi. Endi
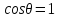 .
Shunday qilib,
.
Shunday qilib,
 xajmdagi energiya miqdori
xajmdagi energiya miqdori

Shu
sababli,
 fazoviy burchakdan kelayotgan nurlanishning
fazoviy burchakdan kelayotgan nurlanishning
 energiya zichligi
energiya zichligi

va umumiy energiya zichligi barcha yo‘nalishlar bo‘yicha integrallash orqali qo‘lga kiritiladi. Izotrop nurlanish uchun biz quyidagiga ega bo‘lamiz:

Gipparxning
hali noaniq bo‘lgan klassifikatsiyasi 1856 yilda Norman R. Pogson
tomonidan o‘zgartirilgan edi. Yangi, kattaroq aniqlikdagi
sinflashtirish oldingiga iloji boricha mos keladi, ammo natijada,
astronomiyaga hos bo‘lgan, nomantiqiy ta’riflar bartaraf etildi.
Shunday qilib, endi birinchi sinfdagi yulduzlarning ravshanligi
oltinchi sinfdagi yulduzlarning ravshanligidan yuz marta kattaroq deb
qabul qilindi. Pogson
 va
va
 sinflarning ravshanliklari orasidagi nisbatni
sinflarning ravshanliklari orasidagi nisbatni
 deb
ta’riflaydi.
deb
ta’riflaydi.
Ravshanlik
sinfi yoki yulduz
kattalik
kuzatiladigan oqim zichligi (
( )
birligida belgilanishi mumkin. 0 ga teng yulduz kattaligi oldindan
tanlangan
)
birligida belgilanishi mumkin. 0 ga teng yulduz kattaligi oldindan
tanlangan
 oqim zichligiga mos keladi deb qabul qildik. Shunda barcha boshqa
yulduz kattaliklari quyidagi tenglama orqali topiladi:
oqim zichligiga mos keladi deb qabul qildik. Shunda barcha boshqa
yulduz kattaliklari quyidagi tenglama orqali topiladi:

Tenglamadagi koeffitsient 2.512 emas, balkim aynan 2.5 ligini yodda tuting! Yulduz katataligi o‘lchovsiz birlik, ammo o‘quvchilarga aynan qasi kattalik haqida gap ketayotigani to‘g‘risida eslatib turish uchun biz buni, masalan 5 mag yoki 5m deb yozishimizz mumkin.
(4.8)
tenglamasi Pogson ta’rifiga ekvivalentligini ko‘rishimiz muimkin.
Agarla ikkita yulduzning yulduz kattaliklari
 va
va
 va ularning oqim zichliklari mos ravishda
va ularning oqim zichliklari mos ravishda
 va
va
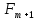 bo‘lsa, unda
bo‘lsa, unda

bu
erdan kelib chiqadi.
kelib chiqadi.
Xuddi
shu yo‘l bilan ikkita yulduzning
 va
va yulduz kattaliklari va ularning
yulduz kattaliklari va ularning
 va
va oqim zichliklari quyidagicha bir biri bilan bog‘langanligini
ko‘rsatishimiz mumkin:
oqim zichliklari quyidagicha bir biri bilan bog‘langanligini
ko‘rsatishimiz mumkin:

Yulduz kattaliklar orinilan oltita sinfga nisbatan ikkala tomonga kengaygan.Eng ravshan yulduz Siriusning yulduz kattaligi manfiy bo‘lib, –1.5 ga teng. Quyoshning yulduz kattaligi –26.8, to‘liq Oyniki esa –12.5. Kuzatiladigan eng hira obyektlarning yulduz kattaliklari teleskopning o‘lchamiga, qabul qilgichning sezgirligiga va ekspozitsiya vaqtiga bog‘liq. Bu chegara eng hira tomonga tobora siljib kelmoqda; hozirgi kunda kuzatiladigan eng hira obyektlarning yulduz kattaligi 30mdan oshgan.
Kurinma yulduz kattaliklari yulduzlarning asli yorqinliklari haqida hech narsani bildirmaydi, chunki ular turli masofalarda joylashgan. Yulduzning o‘ziga xos ichki ravshanlikning miqdoriy o‘lchash natijasi absolyut yulduz kattaligi deyiladi. Bu kattalik kuzatuvchiga nisbatan yulduzning 10 parsek masofadagi ko‘rinma yulduz kattaligi deb ta’riflanadi (4.6-rasm).

4.6-rasm.
Hozir
biz ko‘rinma yulduz kattaligi
 ,
absolyut yulduz kattaligi
,
absolyut yulduz kattaligi
 va
masofa
va
masofa
 larni
bog‘lovchi tenglamani eltirib chiqamiz. Yulduzdan
larni
bog‘lovchi tenglamani eltirib chiqamiz. Yulduzdan
 fazoviy burchakdan chiquvchioqim,
fazoviy burchakdan chiquvchioqim,
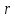 masofada
masofada
 yuzasi bo‘yicha taqsimlanganligi uchun oqim zichligi masofa
kvadratiga teskari proporsionaldir. Shuning uchun,
yuzasi bo‘yicha taqsimlanganligi uchun oqim zichligi masofa
kvadratiga teskari proporsionaldir. Shuning uchun,
 masofadagi
masofadagi
 oqim
zichligining 10 parsek masofadagi
oqim
zichligining 10 parsek masofadagi
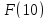 oqim
zichligiga nisbati quyidagicha bo‘ladi:
oqim
zichligiga nisbati quyidagicha bo‘ladi:
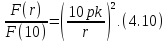
Shunday
qilib,
 va 10 pk masofalardagi yulduz kattaliklari orasidagi ayirma, yoki
boshqacha qilib aytganda
va 10 pk masofalardagi yulduz kattaliklari orasidagi ayirma, yoki
boshqacha qilib aytganda
 masofa
moduli:
masofa
moduli:

yoki

Ma’lum bir tarixiy sabablarga ko‘ra bu tenglama deyarli har doim quyidagicha yozilib

faqatgina parsek birligida ifodalangan masofalarga haqiqiydir. (O‘lchamli qiymatning logariflash, asli olganda, fizika nuqtai nazaridan absurddir –mantiqga ega emas). Ba’zi hollarda masofa kiloparsek yoki megaparseklarda berilishi mumkin, bunda (4.12)dagi konstantalar o‘zgarishi kerak albatta. Bundan qochish uchun biz aynan (4.11)dagi formuladan foydalanishni tavsiya etamiz.
Absolyut
bolometrik yulduz kattaligini yorqinlik birligida ifodalash mumkin.
 =
10 pk masofadagi umumiy oqim zichligi
=
10 pk masofadagi umumiy oqim zichligi
 bo‘lsin, xuddi shu kattalik
bo‘lsin, xuddi shu kattalik
 Quyosh
uchun bo‘lsin. Yorqinlik
Quyosh
uchun bo‘lsin. Yorqinlik
 bo‘lganligi
sababli, quyidagiga ega bo‘lamiz:
bo‘lganligi
sababli, quyidagiga ega bo‘lamiz:

yoki

Absolyut
bolometrik yulduz kattaligi
 bo‘lgan
holati yorqinlik
bo‘lgan
holati yorqinlik
 ga mos keladi.
ga mos keladi.


 yuza elementi
yuza elementi
 dan
dan
 fazoviy burchagda
fazoviy burchagda
 yo‘nalishda o‘tayotgan energiyaga bog‘liq.
yo‘nalishda o‘tayotgan energiyaga bog‘liq.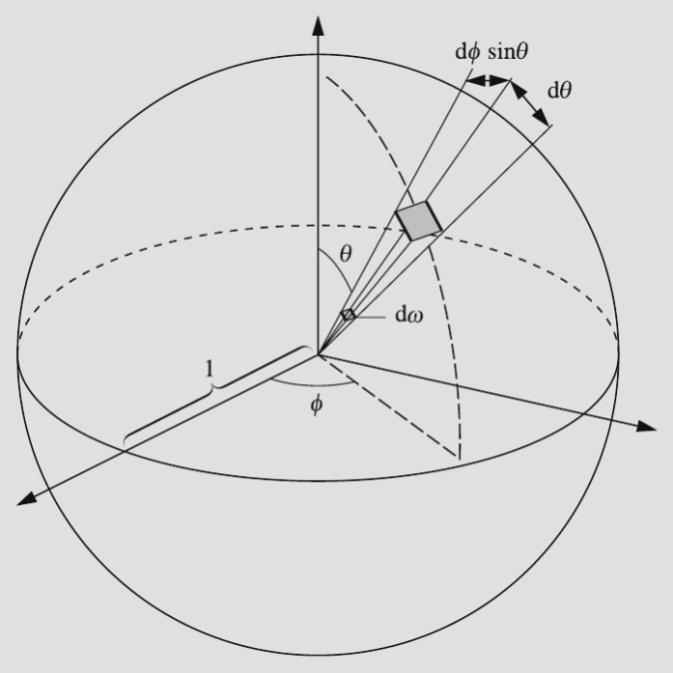
 birlik sferadagi unga mos yuza elementiga teng:
birlik sferadagi unga mos yuza elementiga teng:

 masofada
masofada yuza bo‘yicha taqsimlangan energiya oqimi
yuza bo‘yicha taqsimlangan energiya oqimi
 masofada
masofada
 yuza bo‘ylab tarqaladi.
yuza bo‘ylab tarqaladi.
 fazoviy burchakdan kelayotgan nurlanishni kuzatadi. Manba
uzoqlashganda ushbu fazoviy burchak ostida nurlovchi sohaning
yuzasi kattalashadi
fazoviy burchakdan kelayotgan nurlanishni kuzatadi. Manba
uzoqlashganda ushbu fazoviy burchak ostida nurlovchi sohaning
yuzasi kattalashadi
 .
Shuning uchun siriy ravshanlik yoki birlik fazoviy burchakga
to‘g‘ri keladigan oqim zichligi doimiy (konstanta) bo‘lib
qoladi.
.
Shuning uchun siriy ravshanlik yoki birlik fazoviy burchakga
to‘g‘ri keladigan oqim zichligi doimiy (konstanta) bo‘lib
qoladi.
 vaqt davomida nurlanish
vaqt davomida nurlanish
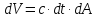 xajmni
egallaydi. Bu erda
xajmni
egallaydi. Bu erda
 nurlanish tarqalayotgan yo‘nalishga perpendekulyar bo‘lgan
sirt elementi.
nurlanish tarqalayotgan yo‘nalishga perpendekulyar bo‘lgan
sirt elementi.