§ 1.12. Sferik uchburchak: sferik trigonometriyaning asosiy formulalari

Astronomiyaning ko‘pgina masalalarini qaraganimizda osmon sferasidan foydalanganimiz uchun osmon jismlarining ko‘rinma va haqiqiy harakatlari bilan bog‘liq bo‘lgan ko‘p masalalarni echish sferik uchburchak xossalari va formulalariga tayanadi. Sferaning biror katta aylanasi tekisligi bo‘ylab yotmaydigan uch nuqtasi orqali o‘tkazilgan katta aylanalarning kesishishidan hosil bo‘lgan uchburchak sferik uchburchak deyiladi. Sferik uchburchakning burchagi deb, shu burchakning tashkil etuvchi katta aylana tekisliklari hosil qilgan ikki yokli burchakka aytiladi. Bu sferik burchaklar uning uchlaridan tomonlariga o‘tkazilgan urinmalar orasidagi tekis burchak bilan o‘lchanadi.

Sferik uchburchak sferada yotgan shunchaki ixtiyoriy uchta burchakga ega bo'lgan shakl emas; uning tomonlari katta aylanalarning yoylari bo'lishi kerak. Agarda sferaning radiusi r bo'lsa, AB yoyning uzunligi

bo'ladi, bu yerda c – markazdan qaraganda AB yoyi tashkil etadigan burchak. Bu burchak AB tomonning markaziy burchagi deyiladi. Tomonlarning uzunliklari va markaziy burchaklar bir biriga yagona yo'l bilan o'tgani sababli, tomonlar o'rniga burchaklarni ifodalash qulay. Bu borada, sferaning radiusi sferik trigonometriya tenglamalariga kirmaydi. Bu yerda biz katta (A,B,C) xarflar bilan sferik uchburchakning burchaklarini va ularga qarama-qarshi tomonlarini, yoki aniqroq qilib aytganda, ularga mos markaziy burchaklarni kichik (a,b,c) harflar bilan belgilaymiz.

Sferik uchburchak ichki burchaklarining yig‘indisi 180° katta bulib 540° dan kichik bo‘ladi. Sferik uchburchak ichki burchaklari yig‘indisi va 180° orasidagi farq sferik orttirma deb yuritiladi.

=A+B+C-180° (1.17)

Sferik orttirma bilan sferik uchburchakning yuzi orasida quyidagi bog‘lanish mavjud.

(1.18)

bu erda R-sfera radiusi. Tekislikdagi uchburchak sferik uchburchakdan keskin farq qilganidan uning formulalarini sferik uchburchak uchun qo‘llab bo‘lmaydi.

1.17-rasm. Sferik uchburchak

Shuning uchun sferik uchburchak uchun alohida formulalarni ko‘rib chiqamiz. Uchlari A, B va C nuqtalarda yotgan sferik uchburchak, radiusi R va markazi O nuqtada bo‘lgan sferada yotsin (1.19-rasm). B va C nuqtalaridan o‘tgan radius yunalishlari OB va OC larni A uchidan b va c tomonlariga o‘tkazilgan urinmalar bilan kesishguncha davom ettiramiz. Bu kesishgan nuqtalar (K va L) ni o‘zaro tutashtirib, bir tomoni (KL) umumiy bulgan ikkita teng yonli AKL va OKL uchburchaklarni hosil qilamiz. Bu uchburchaklarning umumiy tomoni KL ning kattaligini har ikkala uchburchakdan alohida-alohida topsak,

AKL dan: (1.19)

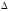OKL dan: (1.20)

(1.20) dan (1.19) ni ayirsak:

(1.21)

Endi AKO va ALO uchburchaklar to‘g‘ri burchakli ekanligidan ulardan topilgan radius

, (1.22)

bo‘ladi. Shuningdek, bu uchburchaklardan:

yoki , yoki

yoki , yoki

Ushbu ifodalarni (1.21) ga qo‘yib ixchamlab, quyidagi tenglamani hosil qilamiz:

va uni 2R² ga bo‘lsak,

yoki

(1.23)

Demak, sferik uchburchakda bir tomonining kosinusi qolgan ikki tomonining kosinuslari bilan shu tomonlar sinuslari va ular orasidagi burchak kosinusiga ko‘paytmasining yig‘indisiga teng bo‘ladi. (1.23) formulani sferik uchburchakning boshqa tomonlari uchun ham yozish mumkin.

(1.24)

(1.25)

Bu tenglamalardan (1.24) formuladagi o‘riniga (1.23) tenglamaning o‘ng tomonini qo‘ysak, u holda:

ga almashgirib barcha haddarini sinc ga bo‘lsak:

yoki

. (1.26)

Shuningdek:

_, (1.26')

, (1.27)

demak, sferik uchburchakda biror tomoni sinusining shu tomonga yopishgan burchak kosinusiga kupaytmasi burchakni chegaralovchi ikkinchi tomon sinusining uchinchi tomon kosinusiga ko‘paytmasidan chegaralovchi tomon kosinusini uchinchi tomon sinusiga va keyingi ikki tomon orasidagi burchak kosinusi ko‘paytmasi ayrilganiga teng. (1.26-1.27) formulalar sferik uchburchak uchun besh elementli formulalari deb yuritiladi. Endi (6) tenglamani sosA ga nisbatan aniqlab, sinuslar formulalarini topamiz.

(1.28)

Ikkala tomonini kvadratga ko‘tarib:

(1.29)

hosil qilamiz. 1 dan (1.29) ning har ikkala tomonini ayirsak:

(1.30)

bu yerda 1-cos²A ni sin²A bilan almashtirib, tenglikning ikkala tomonini sin²a ga bo‘lsak:

yoki

Qavslarni ochib ixchamlasak,

demak

(1.31)

olingan natija a, b, s lar uchun simmetrik bo‘lganidan

Hosil qilingan uchta tenglamalarning o‘ng tomonlari teng bo‘lganidan

(1.32)

ya’ni, sferik uchburchak istalgan burchagi sinusining bu burchak qarshisidagi tomon sinusiga nisbati o‘zgarmas kattalikdir.

Agarda biz a,b va c tomonlari juda kichik (nolga intilishi mumkin degan limit) deb qabul qilsak, unda sferik uchburchak tekislikdagi uchburchakka aylanadi. Agarda hamma burchaklar radiandarda ifodalangan bo'lsa, unda biz quyidagi taxminiy formulalarga ega bo'lamiz:

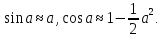(1.33)

Ushbu approksimatsiyalarni kosinuslar formulasiga qo'yish orqali biz tekislik

geometriyasidagi sinuslar formulasiga kelamiz:

(1.34)

Xuddi shu yo'l bilan sferik trigonometriyadagi kosinuslar formulasidan tekislikdagi kosinuslar formulasi

(1.35)

ni keltirib chiqarishimiz mumkin.