26. Формула Тейлора для функции нескольких переменных.

u=f(M), k+1-раз. дифф в опр. т. М₀€[М]

└→(R_k+1(N))

N отр М₀М, u=f(M), k-1 раз.дифф. в окр. k раз дифф в т. М₀.

;

27. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточные условия экстремума.

u=f(M)=f(x₁,x₂,_..,x_n) опред. в окр. т.М₀(x₁⁰,x₂⁰,_..,x_n⁰).

Опр. Ф-ция u=f(M) имеет в т. М₀локальный максимум (мин.), если сущ. такая окр. в т. М₀в кот.при ММ₀выполняется след. нер-во:f(M)<f(M₀), (f(M)>f(M₀)).

∆u=f(M)-f(M₀)<0, если М₀т.локал. мах.; ∆u>0, если М₀т.локал. мin.

Теор.(необход.усл.экстремума).

Если ф-ция u=f(M) дифф. в т.М₀и М₀– т.лок.max(min), то в этой точке:

Док-во: док-ем, что ,u=f(x₁,x₂,_..,x_n)

x₂=x₂⁰, М₀(x₁⁰,x₂⁰,_..,x_n⁰).

x₃=x₃⁰,..

x_n=x_n⁰.

u=f(x₁⁰,x₂⁰,_..,x_n⁰) – имеет лок. экстремум в т.М₀→.

Точка в кот. все частные призвод. u=f(M) – стационарн., таким обр. точками возможен. экстремума дифф. экстремума явл. стационар. т., но в стационар. т. ф-ция может и не иметь экстремума.

u=xy²,u_x’=y²=0;u_y’=2xy=0;M(0,0) стационар., но не явл. т.экстремума.

∆u=u(M)-u(M₀)=xy²>(<)0

Кроме того, лок. экстр. ф-ция может иметь в т., в кот. она не дифф.:

z=1-√x²+y²;z_x’=x/√x²+y²;z_y’=y/√x²+y²;z(0,0)=1;z(∆x,∆y)<1

Теор.(Дост. усл. сущ. т. лок. экстр.)

Пусть u=f(u) дважды непр. дифф. в некот. окр.т.M₀и т.M₀– стационар.т.,u=f(M) (df(M₀)=0), тогда если для любыхdx₁,dx₂,..dx_nне равных одновременно 0:

d²f(M₀)>0, то т.M₀-т.лок.min;d²f(M₀)<0, то т.M₀-т.лок.max;

Д-во: f(M)=f(M₀)+df(M₀)/1!+d²f(N)/2!., ∆f(M₀)=f(M)-f(M₀)=df(M₀)+d²f(N)/2!.

u=f(M) – дважды непр. дифф.,d²f(M₀)>0→d²f(N)>0;d²f(M₀)<0→d²f(N)<0;→ ∆f(M₀)>0→

M₀ – т.лок.min;M₀ – т.лок.max;

1. d²f(M₀)>0↔a₁₁>0,

2. d²f(M₀)<0↔a₁₁<0,

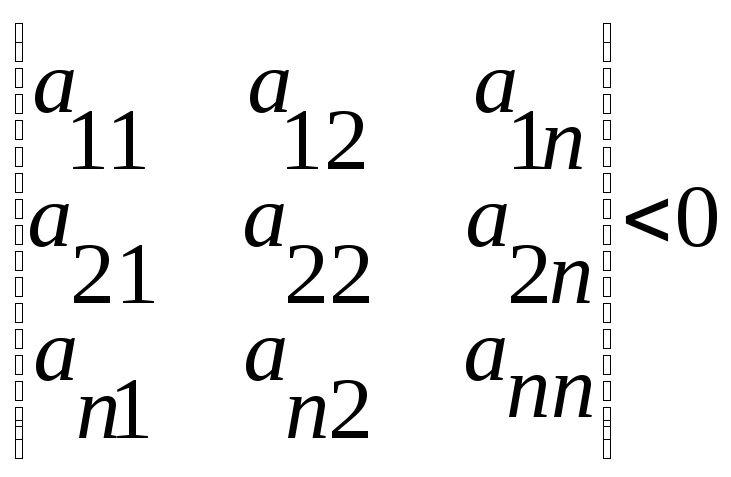
Если d²f(M₀) представляет собой закономерную квадрат. форму, то в т.M₀экстремума не будет. Если 2-ой дифф. представляет собой квадр. форму

Q(dx₁,dx₂,..dx_n)>0 то полож.опр.

Q(dx₁,dx₂,..dx_n)≥0 то казизнакополож.опр

х₁²+2х₁²х₂²+х₂²+(х₁+х₁)²≥0; х₁=-х₂.

28. Условный экстремум функции нескольких переменных. Метод множителей Лагранжа. Наибольшее и наименьшее значения непрерывной функции в замкнутой области.

Найти экстремум z, при ксловии, что x и y связаны следующим образом.

; x+y-1=0;

(*)

; ;;

Метод множителя Ла-Гранджа.

(*) эквивалентна задаче: , где

-множитель Ла-Гранджа; - функция Ла-Гранджа.

Надо исследовать ф-ции Ла-Гранджа с учетом условия связи в диффиринциалах.

Наибольшее и наименьшее значение ф-ции в замкнутой области.

Если ф-я определена в замкнутой ограниченной области Д, то она достигает своего min и max значения, либо в стационарных точках внутри области, либо на ее границе.

29. Интегралы по фигуре от скалярной функции, их свойства, геометрические и физические приложения.

Множество называется связанным, если любые 2 из них можно соединить линией, все точки которой принадлежат данному множеству.

Под геометрической фигуройпонимается одно из следующих связных (включая границу) множеств точек (см. таблицу).

Диаметром d фигуры Ф называется максимальное расстояние между двумя ее точками.

Под меройфигуры Ф понимается следующее (см. таблицу).

Если он существует, конечен и не зависит от способа построения интегральной суммы , то он называется интегралом по фигуре Ф от скалярной ф-ции Ф(Р) и обозначается

Теорема: Если на связной, ограниченной и содержащей граничные точки фигуре Ф скалярная ф-ция f(P) непрерывна, то интеграл по фигуре Ф существует.