
№1. Векторы в пространстве, их свойства.
Линейные операции над векторами.
В математике различают скалярные и векторные величины. Скалярные величины полностью определяются своим значением, например, температура тела, масса, объем и т.д. Но для силы, скорости, ускорения, кроме величины надо указать еще и направление в пространстве. Такие величины называют векторными. Отметим также, что с математической точки зрения вектором можно назвать любой объект, а не только направленный отрезок. Лишь бы были определены операции их сложения и умножения на число.
Вектором называется направленный отрезок AB с начальной точкой A и конечной точкой B, обозначается AB. Будем считать, что два вектора AB и CD равны, если они одинаково направлены и длины отрезков AB и CD равны |CD|=|AB|.
Cвободные векторы это такие векторы, которые можно перемещать параллельно самим себе.
Нулевым называется вектор, начало, и конец которого совпадают.
Длина нулевого вектора равна нулю, и ему можно принимать любое направление.
Длиной или нормой вектора AB называется длина отрезка AB и обозначается |AB|.
Вектор a, длина которого равна 1, называется единичным или ортом.
Векторы, параллельные одной прямой, называются коллинеарными. Векторы, параллельные одной плоскости, называются компланарными.
Суммой двух векторов a и b называется вектор b+a.
Суммой конечного числа n векторов a1,a2,…,an называется замыкающий вектор OAn.
Вектор (-b) называется противоположным вектору b, если (−b)||b,||- b||=||b|| и его направление противоположно вектору b.
Разностью двух векторов a и b называется вектор a−b, являющийся суммой векторов a и (-b ).
Произведением вектора a на действительное число α называется вектор b=aα, длина которого |b|=|aα|=|a||α|, а направление совпадает с a, если 0<λ и противоположно a, если 0>α.
Введенные операции сложения векторов и умножения на число называются линейными и обладают свойствами коммутативности, ассоциативности и дистрибутивности:
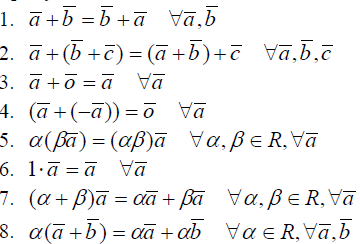
№2. Линейная зависимость и линейная независимость векторов. Базис. Представление векторов в базисе
Линейной комбинацией называется множество векторов вида:
![]() .
Исходное множество
.
Исходное множество
![]() ,
,
![]() .
.
Теорема: векторное множество будет линейно-независимым, если линейная комбинация этих векторов обращается 0, когда действительные множители равны 0 (ни один из векторов не выражается через другие).
![]()
Любые 4 вектора в пространстве линейно независимы.
Базисом на прямой называется любой ненулевой вектор на этой прямой.
Базисом на плоскости называются любые 2 линейно независимых вектора, взятые в определенном порядке.
Базисом в пространстве называются любые 3 линейно независимых вектора, взятые в определенном порядке.
Выражение
![]() называется разложением вектора по
базису. Числа
называется разложением вектора по
базису. Числа![]() и
и![]() называются
координатами вектора а в базисе e1
и e2.
называются
координатами вектора а в базисе e1
и e2.
Основное значение базиса заключается в том, что вместо выполнения линейных операций над векторами можно выполнять операции над их координатами.
№3. Скалярное произведение двух векторов, его свойства. Вычисление в декартовой системе координат.
Скаля́рное
произведе́ние
— операция над двумя векторами,
результатом которой является скаляр
(число), не зависящее от системы координат
и характеризующее длины векторов-сомножителей
и угол между ними.
![]()
Свойства:
1. Переместительное: ab=ba
2.
Ассоциативность:
![]()
3.
Дистрибутивность:
![]()
4.
![]()
5.
![]()
Вычисление: a*b = x1x2 + y1y2 + z1z2
№4. Векторное произведение двух векторов, его свойства, Вычисление в декартовой системе координат. Геометрический смысл.
Векторным
произведением
вектора a
на вектор b
называется вектор c,
удовлетворяющий следующим требованиям:
длина вектора c
равна произведению длин векторов a и b
на синус
угла φ;
между ними
![]() *вектор c ортогонален
каждому из векторов a и b *вектор c направлен
так, что тройка векторов abc является
правой.
Обозначение:
*вектор c ортогонален
каждому из векторов a и b *вектор c направлен
так, что тройка векторов abc является
правой.
Обозначение:
![]()
Геометрически
векторное произведение
![]() есть
ориентированная площадь параллелограмма,
построенного на векторах
есть
ориентированная площадь параллелограмма,
построенного на векторах
![]() ,
представленная псевдовектором,
ортогональным этому параллелограмму.
,
представленная псевдовектором,
ортогональным этому параллелограмму.
Свойства
векторного произведения:1)При
перестановке сомножителей векторное
произведение меняет знак (антикоммутативность),
т.е![]() 2)Векторное
произведение обладает сочетательным
свойством относительно скалярного
множителя, то есть
2)Векторное
произведение обладает сочетательным
свойством относительно скалярного
множителя, то есть![]() 3)Векторное
произведение обладает распределительным
свойством:
3)Векторное
произведение обладает распределительным
свойством:![]() Если два вектора a
и b
определены своими прямоугольными
декартовыми координатами, а говоря
точнее — представлены в ортонормированном
базисе
Если два вектора a
и b
определены своими прямоугольными
декартовыми координатами, а говоря
точнее — представлены в ортонормированном
базисе![]()
![]() а система координат правая, то их
векторное произведение имеет вид
а система координат правая, то их
векторное произведение имеет вид
![]() Для
запоминания этой формулы удобно
использовать определитель:
Для
запоминания этой формулы удобно
использовать определитель:![]() или
или![]() где
где
![]() —
символ
Леви-Чивиты. Геометрические
свойства векторного произведения
1)Необходимым
и достаточным условием коллинеарности
двух векторов является равенство нулю
их векторного произведения.2)Модуль
векторного произведения
—
символ
Леви-Чивиты. Геометрические
свойства векторного произведения
1)Необходимым
и достаточным условием коллинеарности
двух векторов является равенство нулю
их векторного произведения.2)Модуль
векторного произведения
![]() равняется
площади S параллелограмма,
построенного на приведённых к общему
началу векторах a
и b(см.
Рисунок 1)3)Если e —
единичный
вектор, ортогональный векторам a
и b,
а S —
площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:
равняется
площади S параллелограмма,
построенного на приведённых к общему
началу векторах a
и b(см.
Рисунок 1)3)Если e —
единичный
вектор, ортогональный векторам a
и b,
а S —
площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:![]() 4)Если
c —
какой-нибудь вектор, π —
любая плоскость, содержащая этот вектор,
e —
единичный вектор, лежащий в плоскости
π
и ортогональный к c,
g —
единичный вектор, ортогональный к
плоскости π
и направленный так, что тройка векторов
ecg
является правой, то для любого лежащего
в плоскости π
вектора a
справедлива формула
4)Если
c —
какой-нибудь вектор, π —
любая плоскость, содержащая этот вектор,
e —
единичный вектор, лежащий в плоскости
π
и ортогональный к c,
g —
единичный вектор, ортогональный к
плоскости π
и направленный так, что тройка векторов
ecg
является правой, то для любого лежащего
в плоскости π
вектора a
справедлива формула
![]() 5)При использовании скалярного произведения
можно высчитать объём параллелепипеда,
построенного на приведённых к общему
началу векторах a,
b
и c
(см. Рисунок 2). Такое произведение
называется смешанным.
5)При использовании скалярного произведения
можно высчитать объём параллелепипеда,
построенного на приведённых к общему
началу векторах a,
b
и c
(см. Рисунок 2). Такое произведение
называется смешанным.![]()
№5. Смешанное произведение трех векторов, его свойства. Вычисление в декартовой системе координат. Геометрический смысл.
Смешанным произведенем трех векторов a, b, c называется число, равное векторному произведению (a*b), множенному скалярно на вектор c, то есть (a*b)c. Свойства:
-
Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с х а)•b .
-
Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb )•с=а*(bx с).
-
Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba .
-
Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны. Если abc =0 , то а, b и с— компланарны.
Геометрический
смысл
смешанного произведения. Смешанное
произведение 3-х векторов с точностью
до знака равно объёму параллелепипеда,
построенного на этих векторах, как на
рёбрах, т.е.
![]() . Таким образом,
. Таким образом,
![]() и
и
![]() .
Декарт:
.
Декарт:
![]() =
=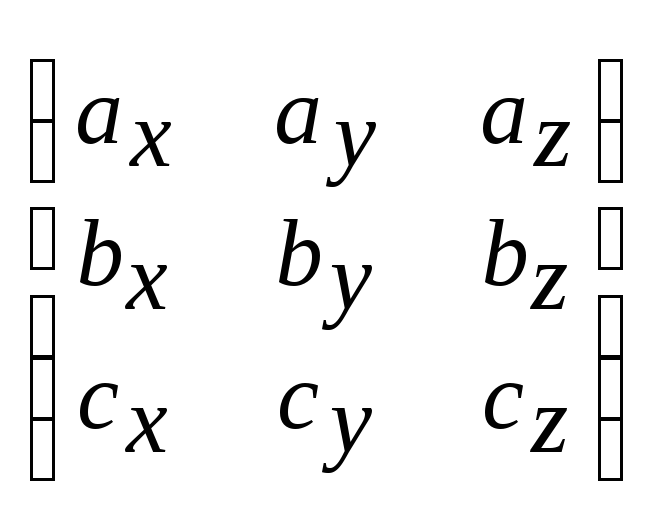
№6. Матрица. Их виды. Линейные операции над матрицами.
Ма́трица
—
математический объект, записываемый в
виде прямоугольной таблицы чисел (или
элементов кольца) и допускающий
алгебраические операции (сложение,
вычитание, умножение и др.) между ним и
другими подобными объектами. Обычно
матрицы представляются двумерными
(прямоугольными) таблицами. Квадратной
называют матрицу, количество строк в
которой равно количеству столбцов.
Треугольная
матрица
— квадратная матрица, в которой все
элементы ниже или выше главной диагонали
равны нулю. Диагональная
матрица
— квадратная матрица, все недиагональные
элементы которой равны нулю.
Обра́тная ма́трица
— такая матрица A-1, при умножении на
которую исходная матрица A даёт в
результате единичную матрицу E:
![]() Нулева́я ма́трица
— это матрица,
размера mxn,
все
элементы которой равны нулю. Разреженная
— в вычислительной математике матрица,
содержащая много нулей. Единичная,
Обратная Перестановочная, Симметричная.
Умножение
матрицы A на число λ
(обозначение: λA) заключается
в построении матрицы B, элементы которой
получены путём умножения каждого
элемента матрицы A на это число, то есть
каждый элемент матрицы B равен bij
= λaij.
Сложение
матриц A
+ B
есть операция нахождения матрицы C,
все элементы которой равны попарной
сумме всех соответствующих элементов
матриц A
и B,
то есть каждый элемент матрицы C
равен cij
= aij
+ bij
Вычитание
матриц A − B
определяется аналогично сложению, это
операция нахождения матрицы C, элементы
которой cij
= aij
– bij
Нулева́я ма́трица
— это матрица,
размера mxn,
все
элементы которой равны нулю. Разреженная
— в вычислительной математике матрица,
содержащая много нулей. Единичная,
Обратная Перестановочная, Симметричная.
Умножение
матрицы A на число λ
(обозначение: λA) заключается
в построении матрицы B, элементы которой
получены путём умножения каждого
элемента матрицы A на это число, то есть
каждый элемент матрицы B равен bij
= λaij.
Сложение
матриц A
+ B
есть операция нахождения матрицы C,
все элементы которой равны попарной
сумме всех соответствующих элементов
матриц A
и B,
то есть каждый элемент матрицы C
равен cij
= aij
+ bij
Вычитание
матриц A − B
определяется аналогично сложению, это
операция нахождения матрицы C, элементы
которой cij
= aij
– bij
№7. Умножение матриц. Транспонирование матриц.
Транспонирование матриц
Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
Свойства транспонированной матрицы:
-
(AT)T=A
-
Линейность: (A+B)T = AT+BT
-
Умножение на число: (xA)T = x*(AT)
-
(A*B)T = BT*AT
Умножение матриц
![]() .
.
![]()
Свойства умножения
-
АB != BA
-
0A = A0 = 0
-
ABC = A(BC)
-
(A+B)C = AC + BC
Пример 1. Рассмотрим для начала простейший пример, когда необходимо найти произведение двух матриц А и В размером 2x2, если
![]()
Решение:
![]()
Элементы матрицы С находятся по следующему алгоритму:
Элемент матрицы С, стоящий на первой строке, в первом столбце находится как сумма произведений первой строки матрицы А на первый столбец матрицы В.
![]()
Элемент матрицы С, стоящий на первой строке, во втором столбце находится как сумма произведений первой строки матрицы А на второй столбец матрицы В.
![]()
Элемент матрицы С, стоящий на второй строке, в первом столбце находится как сумма произведений второй строки матрицы А на первый столбец матрицы В.
![]()
Элемент матрицы С, стоящий на второй строке, во втором столбце находится как сумма произведений второй строки матрицы А на второй столбец матрицы В.
![]()
Таким образом, мы получили
![]()
То есть мы получили, что
![]()
№8. Определители n-го порядка. Их свойства и методы вычисления.
Определителем n-го порядка называется число, равное алгебраической сумме всевозможных произведений элементов взятых по одному и только одному из каждой строки и каждого столбца.
Знак каждого слагаемого определяется числом инверсий в перестановках составленных из первых и вторых индексов сомножителей : если оно четное «+», нечетное «-».
Инверсия - когда большее число стоит перед меньшим.
Св-ва определителей:
-
В определителе строки и столбцы равнозначны.
-
Если все Эл-ты в строке или столбце = 0, то определитель =0.
-
Общий множитель строки или столбца можно выносить.
-
Если в определителе переставить местами 2 строки, то знак определителя изменится на противоположный.
-
Если в определителе 2 одинаковых строки/столбца, то определитель =0.
-
Если в определителе 2 строки пропорциональны, то определитель =0.
-
Определитель можно разложить на сумму.
-
Если в определителе некоторая строка/столбец является линейной комбинацией другой строки-столбца, то определитель =0.
-
Если к Эл-ам некоторой строки добавить соотв. Эл-ты другой строки умноженные на число не равное 0, то определитель не изменится.
Минор- определитель полученный из определителя n-го порядка вычеркиванием К каких-то строк и К столбцов.
Теорема Лапласа.
Определитель n-го порядка равен сумме произведений Эл-ов некоторой строки/столбца на их алгебраические дополнения.
Алгебраическое дополнение – Aij=(-1)i+jMij
Определитель треугольного вида равен произведению Эл-ов главной диагонали.
№9. Обратная матрица. Ее свойства и методы вычисления.
Определение: А-1 называется обратной матрице А, если выполняются условия A·A-1= A-1·A=E
Теорема: если для матрицы А существует обратная, то она единственная.
Теорема:
для того, чтобы для квадратной матрицы
А существовала A-1
необходимо и достаточно, чтобы определитель
![]() 0.
Т.е. перед началом вычислений нужно
найти определитель.
0.
Т.е. перед началом вычислений нужно
найти определитель.
Первый способ нахождения ОМ:
-
Находим алгебраические дополнения (АД) для матрицы (aij - Aij). АД: например, А21 – минор, получаемый вычеркиванием 2й строки и 1го столбца
-
Составляем матрицу С = (Aij)T.
-
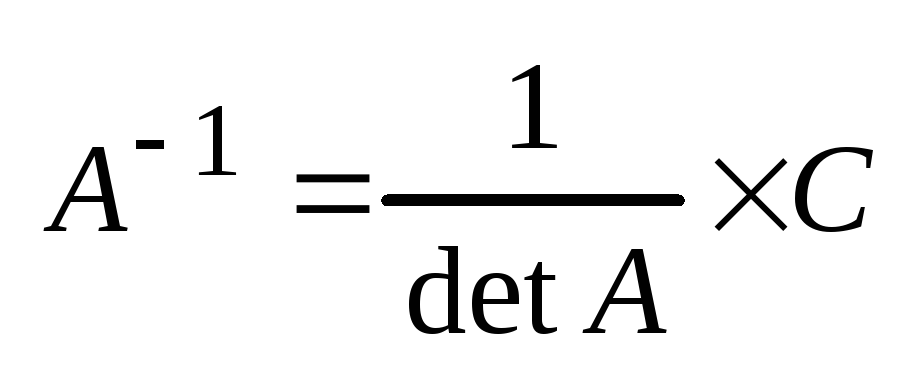
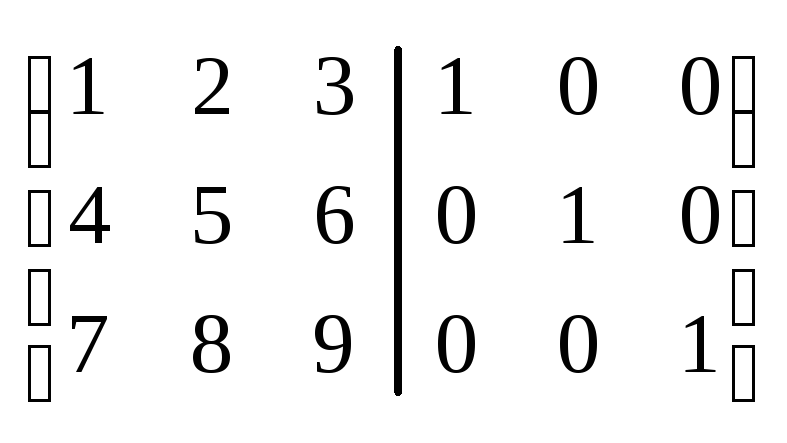
Второй способ:
-
Записываем матрицу (А | E).
-
Приводим левую половину к виду единичной матрицы (Е). Матрица, получившаяся справа будет обратной
Для приведения матрицы к виду единичной используются следующие элементарные преобразования:
-
Перемена местами двух любых уравнений;
-
Умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
-
Прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Свойства ОМ:
-
(A-1) -1 = А
-
(А·B) -1 = B-1·A-1
№10. Ранг матрицы. Методы его вычисления.
Ответ: Рангом матрицы называется наибольший из порядков миноров матрицы , отличных от нуля. Ранг нулевой матрицы считается равным нулю. Ранг невырожденной квадратной матрицы порядка равен, так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля.
Рассмотрим прямоугольную матрицу. Выделим в этой матрице k произвольных строк и k произвольных столбцов (k≤n, k≤m). Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы. Так, у матрицы с тремя строками и пятью столбцами возможны миноры первого, второго и третьего порядка. Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы. Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы: - замены строк столбцами, а столбцов соответствующими строками; - перестановки строк матрицы; - вычеркивания строки, все элементы которой равны нулю; - умножения строки на число, отличное от нуля; - прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число. Сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится.
№11. Метод Гаусса для преобразования матрицы. Его применение для решения задач линейной алгебры.
Метод Гаусса применим для систем т линейных уравнений с п неизвестными:
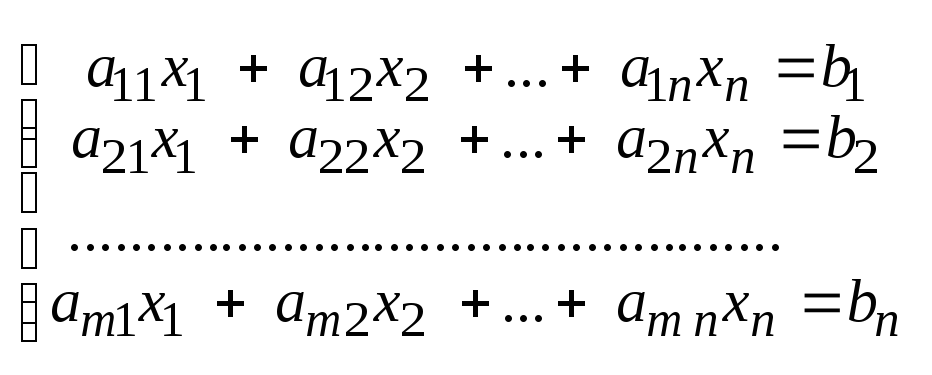
, где x1 , x2, …, xn – неизвестные.
ai j - коэффициенты при неизвестных.
bi - свободные члены (или правые части)
Решения СЛАУ по методу Гаусса состоит из двух этапов.
-
Первый этап (прямой ход метода) – система приводится к треугольному виду.
-
Второй этап (обратный ход) – неизвестные определяются последовательно, начиная с последнего неизвестного (в последнем уравнении) и кончая первым (в первом уравнении).
Для приведения матрицы к треугольному виду используются следующие элементарные преобразования:
-
перемена местами двух любых уравнений;
-
умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
-
прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
После данных преобразований должна получиться треугольная матрица вида:
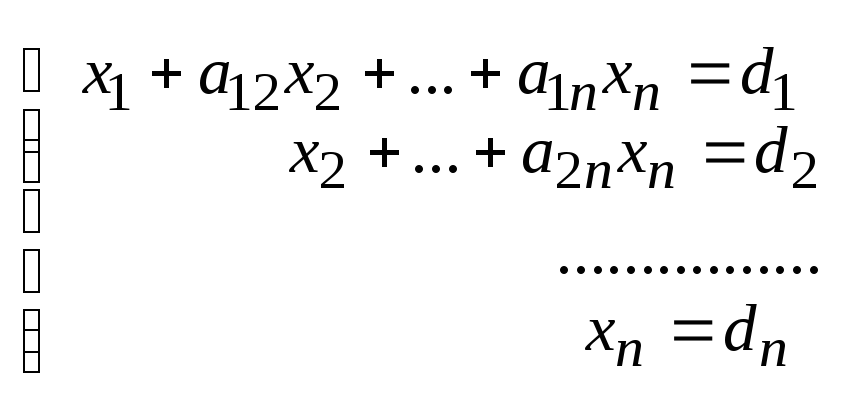 или
или
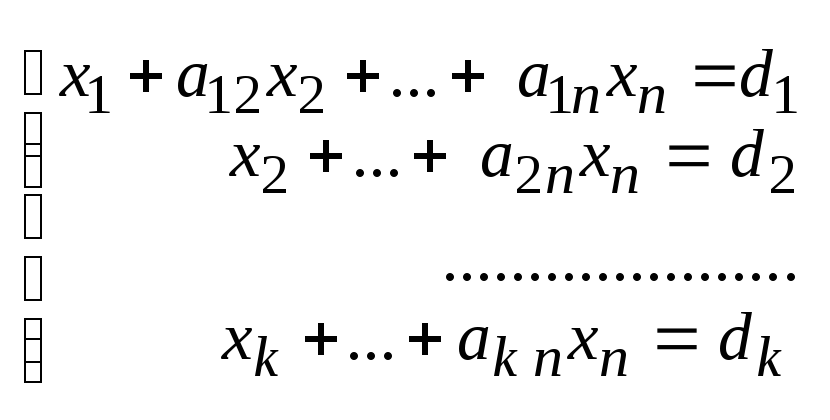
Для первой системы просто последовательно находят значения неизвестных, начиная с нижнего уравнения.
Вторая система будет иметь бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными хk+1, … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находят х1, … , xk, которые будут выражаться через свободные неизвестные.
№12. Предел функции в точке и на бесконечности. Геометрическая интерпретация. Определенности и неопределенности, возникающие при нахождении приделов.
Понятие непрерывности функции непосредственно связано с понятием предела функции.
Число
A называется пределом функции f в точке
a, предельной для множества E, если для
любой окрестности V(A) точки A, существует
такая проколотая окрестность
![]() точки a, что её образ при отображении f
является подмножеством заданной
окрестности V(A) точки A.
точки a, что её образ при отображении f
является подмножеством заданной
окрестности V(A) точки A.
Предел
функции f в точке a, предельной для
множества E, обозначается так:
![]() или
или
![]() ,
если можно опустить упоминание множества
E.
,
если можно опустить упоминание множества
E.
Поскольку
каждой окрестности может быть сопоставлена
своя правильная (симметричная) окрестность,
то определение предела можно сформулировать
на языке
![]() -δ
в том виде, как это принято в математическом
анализе:
-δ
в том виде, как это принято в математическом
анализе:
![]() .
.
Предел функции в точке f в точке a, предельной для множества E, непосредственно связан с пределом последовательности.
Будем
рассматривать всевозможные
последовательности
![]() точек множества E, имеющих своим пределом
точку a, и соответствующие им
последовательности значений
точек множества E, имеющих своим пределом
точку a, и соответствующие им
последовательности значений
![]() функции
в точках последовательности. Если предел
функции функции f в точке a существует,
то этот предел будет пределом каждой
последовательности
функции
в точках последовательности. Если предел
функции функции f в точке a существует,
то этот предел будет пределом каждой
последовательности
![]() .
.
Верно
и обратное: если все последовательности
![]() сходятся
к одному и тому же значению, то функция
имеет предел, равный данному значению.
сходятся
к одному и тому же значению, то функция
имеет предел, равный данному значению.
Другими словами:
![]()
Пределы на бесконечности
Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).
Определения, аналогичные «ε−δ»
Пусть
задана числовая функция с неограниченной
сверху областью определения, то есть
![]() и
и
![]() Число
Число
![]() называется пределом функции f при
называется пределом функции f при
![]() (предел в плюс бесконечности), если
(предел в плюс бесконечности), если
![]()
Пишут:
![]()
Аналогично
пусть
![]() и
и
![]() Число
Число
![]() называется пределом функции f при
называется пределом функции f при
![]() (предел
в минус бесконечности), если
(предел
в минус бесконечности), если
![]()
Пишут:
![]()
Если
пределы в
![]() и
и
![]() существуют
и равны, то говорят что функция имеет
предел в бесконечности:
существуют
и равны, то говорят что функция имеет
предел в бесконечности:
Число
![]() называется
пределом функции f при
называется
пределом функции f при
![]() (предел
в бесконечности), если
(предел
в бесконечности), если
![]()
Неопределенность
![]()
Неопределенности
такого вида возникают при вычислении
пределов типа:
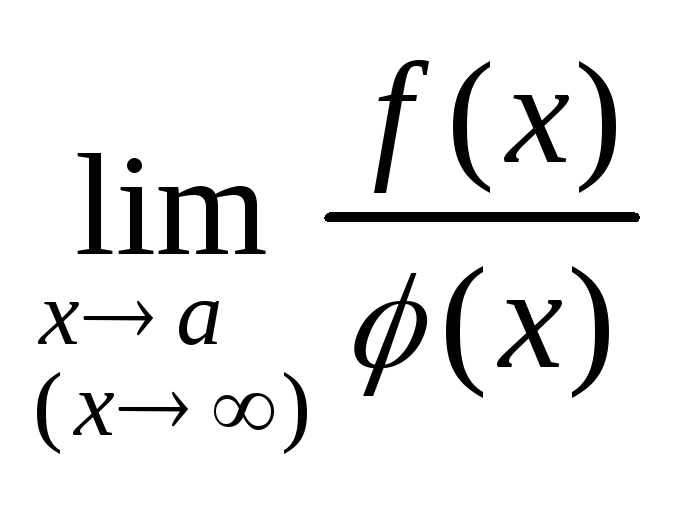 ,
если
,
если

При этом возможны частные случаи:
1)Числитель
![]() и знаменатель
и знаменатель
![]() дроби - многочлены.
дроби - многочлены.
Для вычисления предела необходимо разложить числитель и знаменатель на множители и сократить дробь на множитель, порождающий нуль.
2) Числитель или знаменатель дроби, или оба содержат иррациональность. Для решения примера необходимо освободиться от иррациональности, умножив числитель и знаменатель дроби на сопряженное выражение, сократить дробь на множитель, порождающий нуль.
3) Выражение содержит тригонометрические функции. Для решения примера необходимо путем тригонометрических и алгебраических преобразований свести его к первому замечательному пределу.
Неопределенность
вида
![]()
1)
Числитель и знаменатель дроби при
![]() -
полиномы.
-
полиномы.
Для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень с наивысшим показателем, а затем перейти к пределу.
Неопределенность
вида
![]()
Для
раскрытия этой неопределенности
необходимо путем преобразования
исходного выражения получить
неопределенность вида
![]() или
или
![]() ,
т.е свести к предыдущим случаям
,
т.е свести к предыдущим случаям
Неопределенность
вида
![]()
Этот
случай нахождения предела функции можно
привести к случаю
![]() или
или
![]() путем
преобразования функции к виду дроби.
путем
преобразования функции к виду дроби.
Неопределенность
вида
![]()
Неопределенности такого вида появляются при решении примеров вида:
![]() ,
где
,
где
![]() ,
,
![]() или
или
![]() ,
где
,
где
![]() ,
,
![]() .
.
Преобразуя выражения, сводим их ко второму замечательному пределу.
№13. Методы нахождения предела функции в точке и на бесконечности. Замечательные пределы.
1. Подстановка: при хх0 и х0области определения ф-ции f(x), предел ф-ции f(x)= его частному значению при х=х0
limf(x)=f(x0)
xx0
2. Сокращение: при х и хх0 f(x)/g(x)=0/0, то сокращают числитель и знаменатель на множитель, стремящийся к 0.
3. уничтожение иррациональности (* числитель и знаменатель на 1 число).
4.деление на наивысшую степень х: при х и хх0 f(x)/g(x)=0/0, то делим числитель и знаменатель на наивысшую степень.
5. Приведение к замечательным пределам:
Первый замечательный предел:
![]()
Второй замечательный предел:
![]()
№14. Сравнение функции. Эквивалентные функции. Применение эквивалентных функции к нахождению пределов.
Сравнение функций
![]() при
при
![]() если
если
![]()
![]() при
при
![]() если
существуют интеграл
если
существуют интеграл
![]() ,
содержащий точку a,
и постоянная M,
такие, что
,
содержащий точку a,
и постоянная M,
такие, что
![]()
Локально эквивалентные функции:
![]() при
при
![]() если
если
![]()
Некоторые
эквивалентности
(при![]() ):
):
![]()

![]()
![]()

![]()
![]()
![]()
![]()

![]()
![]()
![]()
Применение эквивалентных функции к нахождению пределов

![]()

![]()
№15. Асимптоты функции
Асимптота — некоторая прямая, к которой данная кривая неограниченно приближается.
Виды асимптот:
Вертикальная асимптота — прямая вида x=a при условии существования предела Lim x→a f(x)=∞
Горизонтальная асимптота — прямая вида y=a при условии существования предела Lim x→±∞f(x)=a
Наклонная асимптота — прямая вида y=kx+b при условии существования пределов Limx→±∞(f(x)/x)=a, Lim x→±∞(f(x)-kx)=b.
Пусть ф. f (x) определена для x а (x а). Если существуют такие числа k и l, что f(x) kx l = 0 при х (х), то прямая y = kx + l - асимптота графика функции f (x) при x (х ).
№16. Непрерывность функции в точке и на отрезке. Односторонняя непрерывность. Классификация точек разрыва.
№17. Производная функции в точке и на отрезке. Геометрический и механический смысл.
Производная функции в точке
Пусть
дана
![]() определена в окрестности
определена в окрестности
![]() .
Рассмотрим
.
Рассмотрим
![]()
![]()
![]()
![]()
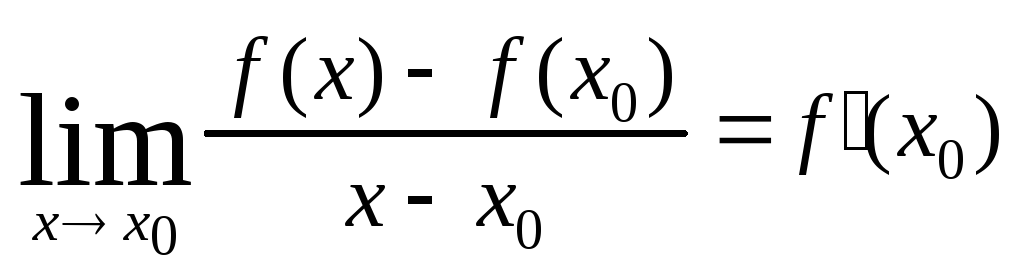
Если
этот предел существует, то он называется
производной
функции f
в точке
![]() .
.
![]()
Производная
функции
– предел отн6ошений приращения функции
к приращению аргумента, при приращении
аргумента
![]() .
.
Операция вычисления или нахождения производной в точке называется дифференцированием.
Производная функции на отрезке
Если
существует
![]() ,
то функция дифференцируема.
,
то функция дифференцируема.
Если
функция
![]() дифференцируема в любой точке отрезка,
то функция дифференцируема на отрезке
дифференцируема в любой точке отрезка,
то функция дифференцируема на отрезке
![]() .
.
![]()
![]()
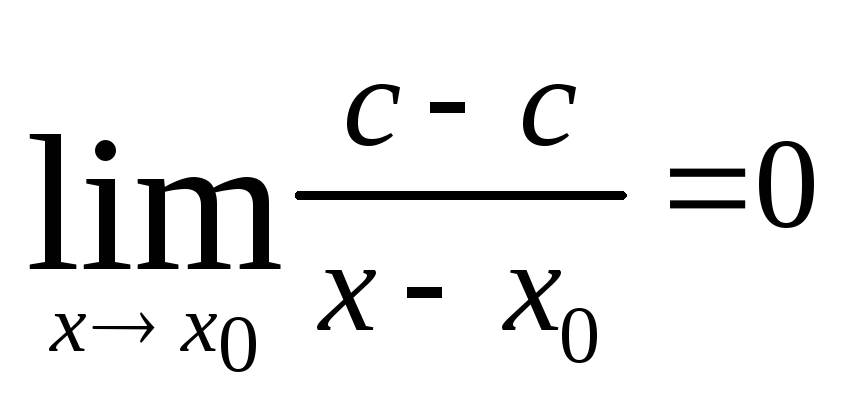
Г еометрический
смысл производной
еометрический
смысл производной
![]()
![]()

![]()
Механический смысл производной
Пусть
материальная точка движется прямолинейно
вдоль прямой, тогда
![]() Найдем среднюю скорость
Найдем среднюю скорость
![]()

№18. Основные методы нахождения производной функции.
Производной
функции f(x)
в точке х=х0
называется отношение приращения функции
![]() в
этой точке к приращению
в
этой точке к приращению
![]() аргумента,
при стремлении последнего к нулю.Нахождение
производной называется дифференцированием.
Вычисление производной функции
аргумента,
при стремлении последнего к нулю.Нахождение
производной называется дифференцированием.
Вычисление производной функции
![]() производится
по общему правилу дифференцирования:
Обозначим f(x)
= u,
g(x)
= v-
функции, дифференцируемые в точке
х.
Основные
правила дифференцирования
1)
производится
по общему правилу дифференцирования:
Обозначим f(x)
= u,
g(x)
= v-
функции, дифференцируемые в точке
х.
Основные
правила дифференцирования
1)
![]() (производная
суммы равна сумме производных) 2)
(производная
суммы равна сумме производных) 2)
![]() (отсюда,
в частности, следует, что производная
произведения функции и константы равна
произведению производной этой функции
на константу)
3)
Производная частного:
(отсюда,
в частности, следует, что производная
произведения функции и константы равна
произведению производной этой функции
на константу)
3)
Производная частного:
![]() ,
если g
0 4) Производная сложной функции:
,
если g
0 4) Производная сложной функции:
![]() 5) Если функция задана параметрически:
5) Если функция задана параметрически:![]() ,
то
,
то
![]() Отношение
Отношение
![]() называется
логарифмической
производной
функции f(x).
Способ логарифмического
дифференцирования состоит
в том, что сначала находят логарифмическую
производную функции, а затем производную
самой функции по формуле
называется
логарифмической
производной
функции f(x).
Способ логарифмического
дифференцирования состоит
в том, что сначала находят логарифмическую
производную функции, а затем производную
самой функции по формуле![]() Способ логарифмического дифференцирования
удобно применять для нахождения
производных сложных, особенно показательных
функций, для которых непосредственное
вычисление производной с использованием
правил дифференцирования представляется
трудоемким. Дифференцирование
функций заданных параметрически До
сих пор функция записывалась в явном
виде y=
f(x) и
в неявном F(x,y)=0.
Но
существует еще третий вид аналитического
представления функции - это представление
её в па
раметрической форме
в виде двух уравнений
Способ логарифмического дифференцирования
удобно применять для нахождения
производных сложных, особенно показательных
функций, для которых непосредственное
вычисление производной с использованием
правил дифференцирования представляется
трудоемким. Дифференцирование
функций заданных параметрически До
сих пор функция записывалась в явном
виде y=
f(x) и
в неявном F(x,y)=0.
Но
существует еще третий вид аналитического
представления функции - это представление
её в па
раметрической форме
в виде двух уравнений![]() где
t-
вспомогательная переменная, называемая
параметром. Заметим,
что функция может быть представлена в
параметрической форме различными
способами. Например, функция, записанная
в неявном виде x2
+ y2
= 1 может
быть представлена в явном виде:
где
t-
вспомогательная переменная, называемая
параметром. Заметим,
что функция может быть представлена в
параметрической форме различными
способами. Например, функция, записанная
в неявном виде x2
+ y2
= 1 может
быть представлена в явном виде:
![]() и
в параметрической форм
и
в параметрической форм
![]() Заметим,
что x2
+ y2
= 1 есть
уравнение окружности единичного радиуса
с центром в начале координат. Если
функция задана в явном виде y=f(x),
то всегда можно записать её в неявном
виде y-f(x)=0,
а также в параметрической форме
Заметим,
что x2
+ y2
= 1 есть
уравнение окружности единичного радиуса
с центром в начале координат. Если
функция задана в явном виде y=f(x),
то всегда можно записать её в неявном
виде y-f(x)=0,
а также в параметрической форме![]() Параметрические
уравнения
Параметрические
уравнения![]() и
уравнение F(x,
y)=0
представляют одну и ту же функцию, если
F(x(t),
y(t))=0.Продифференцируем
y
как сложную функцию от x,
т.е. по формуле
и
уравнение F(x,
y)=0
представляют одну и ту же функцию, если
F(x(t),
y(t))=0.Продифференцируем
y
как сложную функцию от x,
т.е. по формуле![]() и
применим формулу, связывающую производные
обратных функций:
и
применим формулу, связывающую производные
обратных функций:
![]() Введя
обозначения
Введя
обозначения![]() ,
,
![]() получим
получим![]()
№19. Логарифмическое дифференцирование. Производная функции заданной параметрически.
Логарифмическое дифференцирование
Пусть
![]() ,
тогда
,
тогда
![]()
![]()
![]()
Параметрическое дифференцирование
![]()
![]()
t – числовой параметр
![]()
![]()
![]() -
радиус
-
радиус
![]()
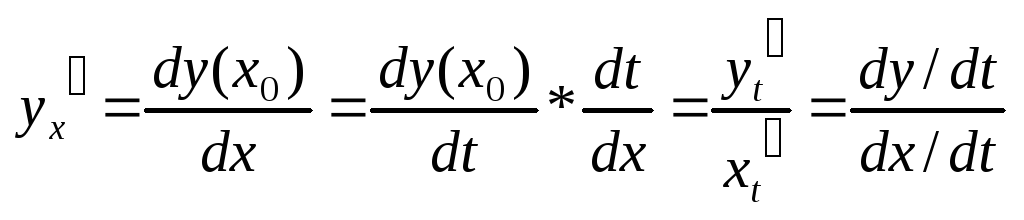
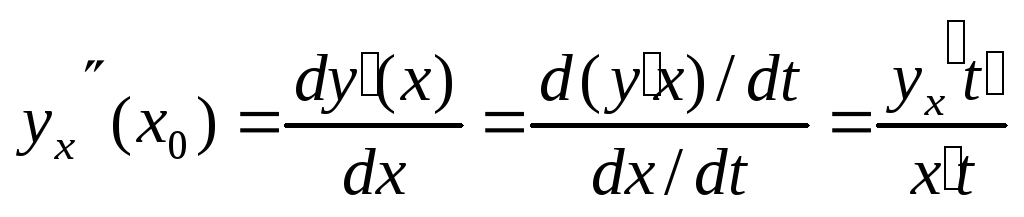
№20. Локальный экстремум функции. Теорема Фирма и теорема Ролля.
Рассмотрим
f(x).
В некоторой точке х0
функция имеет локальный
максимум,
если
![]() (существует U(x)),
что
(существует U(x)),
что
![]() (для каждого х,
принадлежащего U(x0))
выполняется
(для каждого х,
принадлежащего U(x0))
выполняется
![]() .
.
Локальный
минимум:
![]() ,
,
![]() :
:
![]()
Теорема
Ферма.
Пусть
![]() определена
на интервале (а, b),
а
определена
на интервале (а, b),
а
![]() – локальный экстремум, тогда если
– локальный экстремум, тогда если
![]() ,
то
,
то
![]()
Теорема Ролля. Если функция, непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
№21. Локальный экстремум функции: необходимые и достаточные условия
Локальным максимумом ф-ции f(x) называется такое ее значение, которое является наибольшим среди всех значений, принимаемых в некоторой окрестности точки х0
Локальным минимумом ф-ции f(x) называется такое ее значение, которое является наименьшим среди всех значений, принимаемых в некоторой окрестности точки х0.
Условие
![]() является необходимым,
но недостаточным условием наличия
экстремума в точке х0.
является необходимым,
но недостаточным условием наличия
экстремума в точке х0.
Подозрительными на экстремум являются точки, в которых производная равна 0, бесконечности или не существует.
Достаточные условия экстремума:
-
Пусть f(x) дифференцируема в некоторой проколотой окрестности точки х0 и непрерывна в х0, тогда, если
 и х
< х0
или
и х
< х0
или
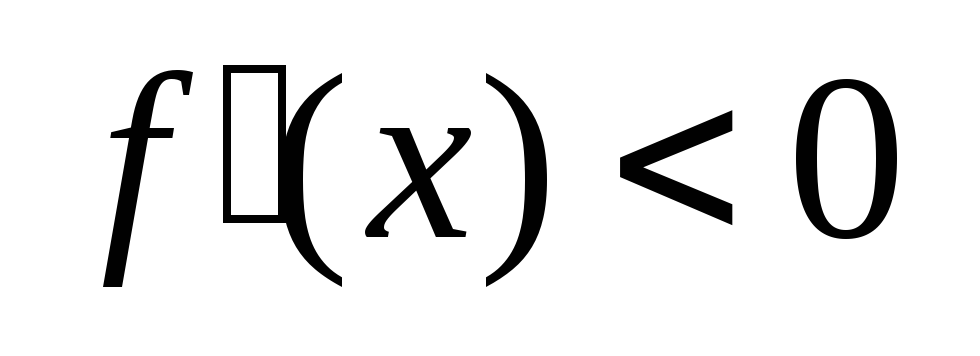 и х
> х0,
то x
–
min;
если
и х
> х0,
то x
–
min;
если
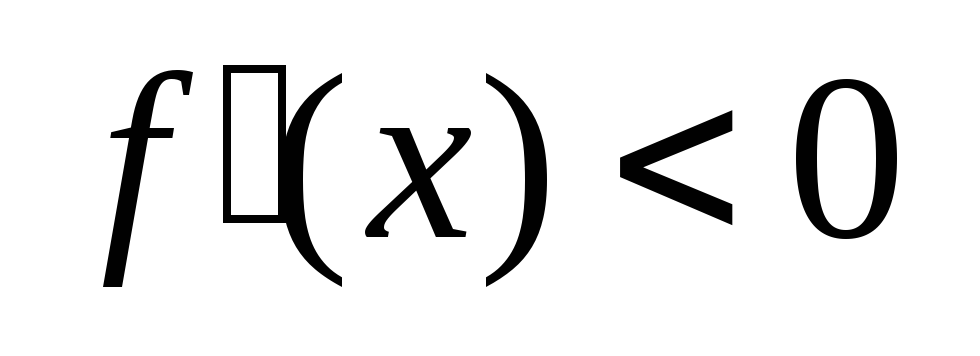 и
х < х0
или
и
х < х0
или
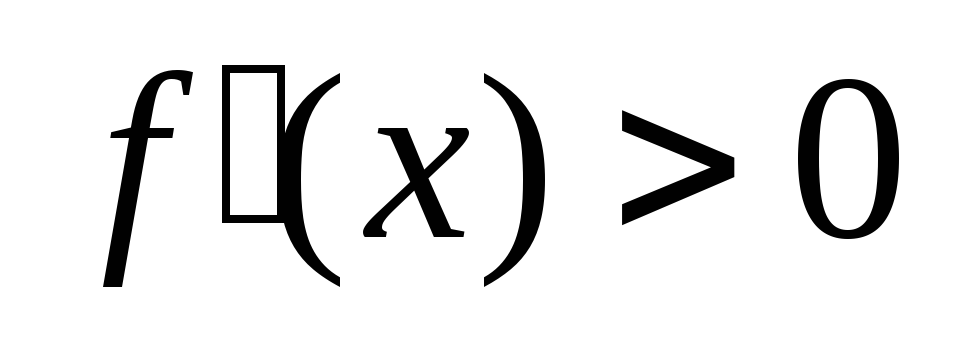 и
х > х0,
то x
– max.
Для проверки этого условия делаем
подстановку значений, меньших и больших
проверяемого x.
и
х > х0,
то x
– max.
Для проверки этого условия делаем
подстановку значений, меньших и больших
проверяемого x. -
Пусть
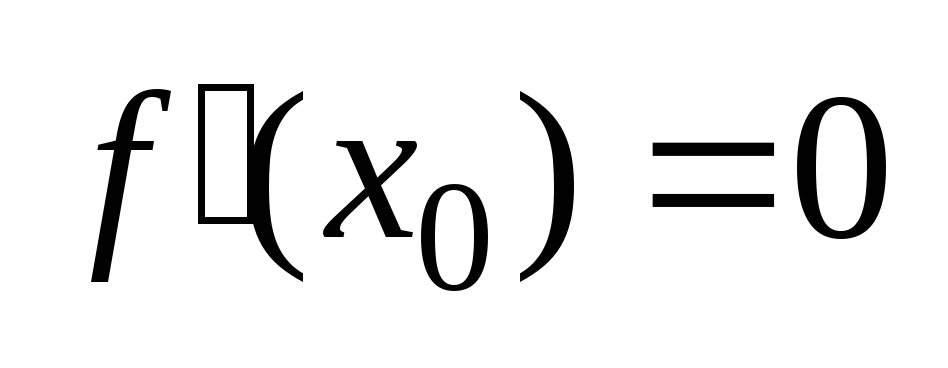 ,
тогда если существует
,
тогда если существует ,
то:
,
то:
если![]() , то х0
– min;
, то х0
– min;
если![]() ,
то х0
– max;
,
то х0
– max;
если
![]() ,
то неизвестно
,
то неизвестно
№22. Теорема Лагранжа (о среднем) и ее следствия
Формула
конечных приращений
или теорема
Лагра́нжа о среднем значении
утверждает, что если функция f
непрерывна на отрезке [a;b]
и дифференцируема в интервале (a;b),
то найдётся такая точка
![]() ,
что
,
что
![]() .
.
Следствие1: Если производная функции равно нулю в каждой точке некоторого промежутка, то функция есть тождественная постоянная в этом промежутке.
Пусть
![]() для всех x
из данного промежутка. Если x0
и x
–две точки этого промежутка, то по
доказанной теореме
для всех x
из данного промежутка. Если x0
и x
–две точки этого промежутка, то по
доказанной теореме
![]() Поскольку
Поскольку
![]() то
то
![]()
![]()
Следствие2: Если две функции имеют разные производные в некотором промежутке. То они отличаются в этом промежутке лишь постоянным слагаемым.
Если,
![]() то
то
![]()
В силу следствия1:
![]()
Среднее
значение функции
— это некоторое число, заключённое
между наименьшим и наибольшим её
значениями. В дифференциальном и
интегральном исчислении имеется ряд
«теорем о среднем», устанавливающих
существование таких точек, в которых
функция или её производная получает то
или иное среднее значение. Наиболее
важной теоремой о среднем значении
функции в дифференциальном исчислении
является теорема Лагранжа (теорема о
конечном приращении): если f(x)
непрерывна на отрезке [a,b]
и дифференцируема в интервале (a,b),
то существует точка c,
принадлежащая интервалу (a,b),
такая, что f(b)
− f(a)
= (b
− a)f'(c).
В интегральном исчислении наиболее
важной теоремой о среднем значении
является следующая: если f(x)
непрерывна на отрезке [a,b],
а
![]() сохраняет
постоянный знак, то существует точка c
из интервала (a,b)
такая, что
сохраняет
постоянный знак, то существует точка c
из интервала (a,b)
такая, что
![]()
В
частности, если
![]() ,
то
,
то
![]()
Вследствие этого под средним значением функции f(x) на отрезке [a,b] обычно понимают величину
![]()
Аналогично определяется среднее значение функции нескольких переменных в некоторой области.
№23. Выпуклость вогнутость функции. Точки перегиба. Необходимые и достаточные условия.
Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 ( a, b ).
Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 ( a, b ).
Достаточное условие вогнутости ( выпуклости ) функции.
Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:
если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
№24. Теорема Кронекера – Капелли. Решение однородных систем линейных алгебраических уравнений. Фундаментальная система решений.
Теорема Кронекера-Капелли: для того, чтобы СЛАУ имела решение (была совместной) необходимо и достаточно, чтобы ранг её расширенной матрицы был равен рангу основной матрицы.
r(A | b) = r(A)
Решение однородных систем. Однородная система всегда совместна, её тривиальным решением является 0-ой вектор.
Для того чтобы СЛАУ имела не 0-ое решение необходимо и достаточно, чтобы r(A) был меньше числа неизвестных (r < n).
Пусть основная матрица А однородной системы уравнений имеет ранг r, тогда эта система уравнений имеет n–r линейно независимых решений.
Совокупность лин. нез. реш. одн. сис. уравнений называется фундаментальной системой решений (ФСР). Общая ФСР может быть записана в виде:
![]()
Алгоритм нахождения ФСР:
-
Составляем расширенную матрицу (А|b), находим её ранг (по Гауссу)
-
Преобразуем систему к эквивалентному виду (из полученной в первом пункте матрицы)
-
Выражаем зависимые переменные через независимые
-
Записываем ФСР
№25. Теорема Кронекера – Капелли. Решение неоднородных систем линейных алгебраических уравнений. Структура общего решения.
Теорема Кронекера-Капелли: для того, чтобы СЛАУ имела решение (была совместной) необходимо и достаточно, чтобы ранг её расширенной матрицы был равен рангу основной матрицы.
r(A | b) = r(A)
Неоднородной системой линейных уравнений называется система вида:
![]()
![]()
Пусть
r(A
| b)
= r(A)
(т.е. система (2) совместна), тогда: если
r
= n,
где n
– число переменных системы (2), то решение
существует и оно единственно; если r
< n,
то общее решение системы (2) имеет вид
![]() ,
где
,
где
![]() —
общее решение системы (1), называемое
общим
однородным решением (ФСР),
—
общее решение системы (1), называемое
общим
однородным решением (ФСР),
![]() —
частное решение системы (2), называемое
частным
неоднородным решением.
—
частное решение системы (2), называемое
частным
неоднородным решением.
№26. Методы решения систем линейных алгебраических уравнений с квадратной основной матрицей .
Системы решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера;3) матричным методом.
