11. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.

Интеграл вида f(t)dt=Ф(x), x[a,b] – интеграл с перем. верхним пределом.

Теорема 1: пусть f(x) непрерыв. на [a,b], тогда Ф(х)=f(t)dt тоже непрерыв. на [a,b]

Док-во: х[a,b] возьмем (х+х) [a,b]. Рассмотрим Ф(х)=Ф(х+х)-Ф(х)= f(t)dt-f(t)dt=f(t)dt+f(t)dt-f(t)dt=f(t)dt=f()х, где [х, х+х].

Ф(х)=f()х.

х0 => Ф(х)0, что означает непрерывность Ф(х) в точке х.

т.к. х – любое, то Ф(х) непрерыв. на [a,b]. ч.т.д.

Теорема 2 (т. Барроу):пусть f(x) непрер. на [a,b], тогда Ф(х)=f(t)dt явл. первообразной для f(x) на [a,b], т.е. (f(t)dt)=f(x)

Производная от интеграла с перем. верхним пределом равна подинтегр. ф-ции от перем. предела.

Док-во: Ф(х)=f()х, где [х, х+х]

(f(t)dt)=Ф (x)=lim_х0 Ф(х)/ х= lim_х0 f()х/х= lim_х0 f() (тогдах) =f(x) ч.т.д

f(х)dх=f(t)dt+С

Пусть F(x) – некот. первообразная для f(x)

Ф(х)=F(х)+С₀

f(t)dt=0

0=Ф(a)=F(а)+С₀ => С₀ = -F(а) => Ф(х)=F(х)-F(а)

Ф(b)=F(b)-F(а)

f(х)dх=F(b)-F(а) – ф-ла Ньютона-Лейбница

Вывод: если f(х) непрер. на [a,b], то для любой ее первообразной F(х) на [a,b] имеет место ф-ла Н.-Л.

12. Замена переменных в определенном интеграле.

Теорема 1 (внесение множителя под знак дифференциала): Пусть u=(x) непрер. дифференцируема на пром-ке с концами a и b; пусть f(u) непрер. на множ-ве значений u=(x) Е().

Тогда f((x)) (х)dx=f(u)du

Док-во: если f(u) имеет первообр. F(u), то f((x)) (х) имеет первообр. F( (x))

f((x)) (х)dx= F( (x)) |^b_a= F( (b)) - F( (a)); f(u)du=F(u) |^(b)_(a)= F( (b)) - F( (a)) ч.т.д.

Теорема 2 (вынесение множителя из-под знака диф-ла): Пусть х=(t) непрер. диф-ма на (,); (t)>0 (=> возрастает) ((t)<0); ()=a; ()=b; пусть f(x) непрер. на пром-ке с концами a и b, тогда

f(х)dх=f((t)) (t)dt

Док-во: g(t)= f((t)) (t); если g(t) имеет первообр. G(t) на (a,b), то f(x) имеет первообр. F(x)=G(^-1(x)) (сущ-ние ^-1(x) гарантировано монотонностью: ^-1(x)>0 (<0)); f((t)) (t)dt= G(t) |^_=G() – G()

f(х)dх=G(^-1(x)) |^b_a=G(^-1(b)) - G(^-1(a))= G() - G() ч.т.д.

13. Интегралы от периодических, нечетных и четных ф-ций.

Теорема: Пусть f(x) интегр. на [-a,a], тогда если f(x) четная, то , если нечетная, то.

Если f(x) – непрерывная с периодом T, интегрируемая на некотором отрезке длины Т, то она интегрируема на любом отрезке длины Т.

Док-во:

Интегрирование по частям в определенном интеграле.

- непр. диф-е ф-ции на

; ;;

14. Вычисление площадей плоских фигур.

1. Вдекартовой системе координат

f(x)-непрерывна

x=a,x=b; отр [a,b] оси оХ

2. Впараметрическом виде.

; ;

разбиваем: ;

3. В полярной системе координат

; ; ; ;

; ;

15. Вычисление длины дуги с помощью определенного интеграла.

Длина ломаной линии, которая соответствует дуге, может быть найдена как

Тогда длина дуги равна

Из геометрических соображений:

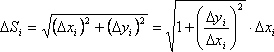
В то же время

Тогда можно показать, что

Т.е.

Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции получаем

где х = j(t) и у = y(t).

Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то

Если кривая задана в полярных координатах, то