
- •Оглавление
- •4. Ограниченность интегрируемой функции 5
- •1. Определенный интеграл. Критерий интегрируемости
- •Понятие определенного интеграла
- •3. Определение определенного интеграла.
- •4. Ограниченность интегрируемой функции
- •5. Суммы Дарбу и их свойства.
- •6. Необходимое и достаточное условие интегрируемости.
- •7. Вычисление определенных интегралов
- •8. Длина дуги
- •Примеры для самостоятельной работы
- •9. Площадь плоской фигуры
- •Примеры для самостоятельной работы
- •10. Вычисление объёмов
- •Задачи для самостоятельного решения.
- •11. Механические и физические задачи.
- •Задачи для самостоятельного решения.
- •Список рекомендуемой литературы
6. Необходимое и достаточное условие интегрируемости.
Теорема. Для того чтобы ограниченная на некотором отрезке функция была интегрируема на этом отрезке, необходимо и достаточно, чтобы
![]() .
(1)
.
(1)
Условие (1)
означает, что для любого
![]() найдется такое
найдется такое
![]() ,
что
,
что
![]() для любого разбиения
для любого разбиения
![]() такого,
что
такого,
что
![]() .
.
Необходимость. Пусть ограниченная на отрезке функция интегрируема на этом отрезке и пусть
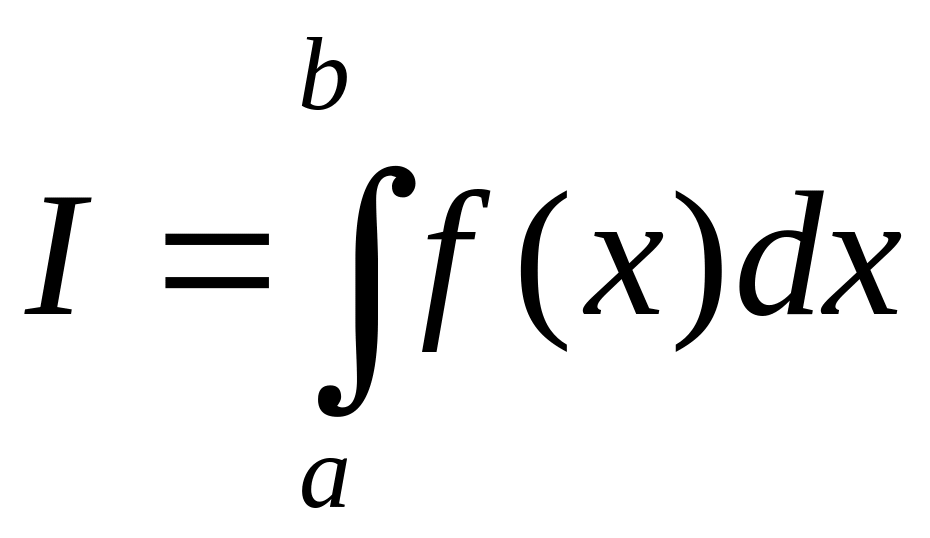 .
.
Тогда для любого
![]() найдется такое
найдется такое
![]() ,
что если
,
что если
![]() ,
то
,
то
![]() .
.
Отсюда согласно свойству 4 интегральных сумм, получим
![]() .
.
Таким образом,
если
,
то
![]() ,
а это означает выполнение условия (1).
,
а это означает выполнение условия (1).
Достаточность.
Пусть функция
ограничена и имеет место (1). Из свойства
5 имеем
![]() ,
поэтому
,
поэтому
![]() .
.
Обозначая их общее
значение через
,
то есть
![]() ,
получим
,
получим
![]() .
.
Отсюда следует
![]() и, в силу свойства 1
и, в силу свойства 1
![]() .
.
Это и означает интегрируемость функции .
Функция, непрерывная на , интегрируема на этом промежутке.
В дальнейшем
понятие определенного интеграла
 будет расширено на неограниченные
функции и на бесконечный промежуток.
будет расширено на неограниченные
функции и на бесконечный промежуток.
7. Вычисление определенных интегралов
a) Формула
Ньютона-Лейбница. Пусть функция
непрерывна на отрезке
и
![]() – ее первообразная, тогда
– ее первообразная, тогда
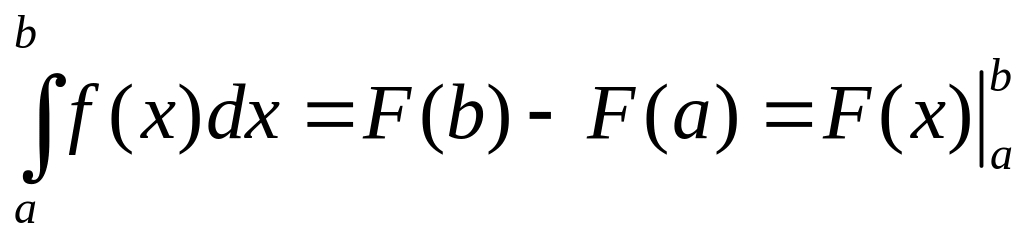 . (1)
. (1)
Пример 1. Вычислить интегралы
a)![]() ,
b)
,
b)![]() ,
c)
,
c)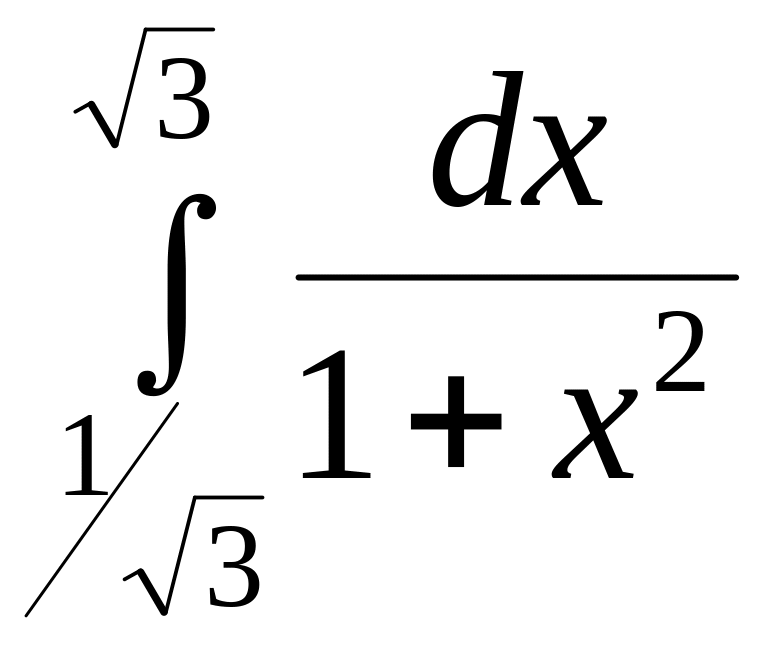 .
.
Для функции
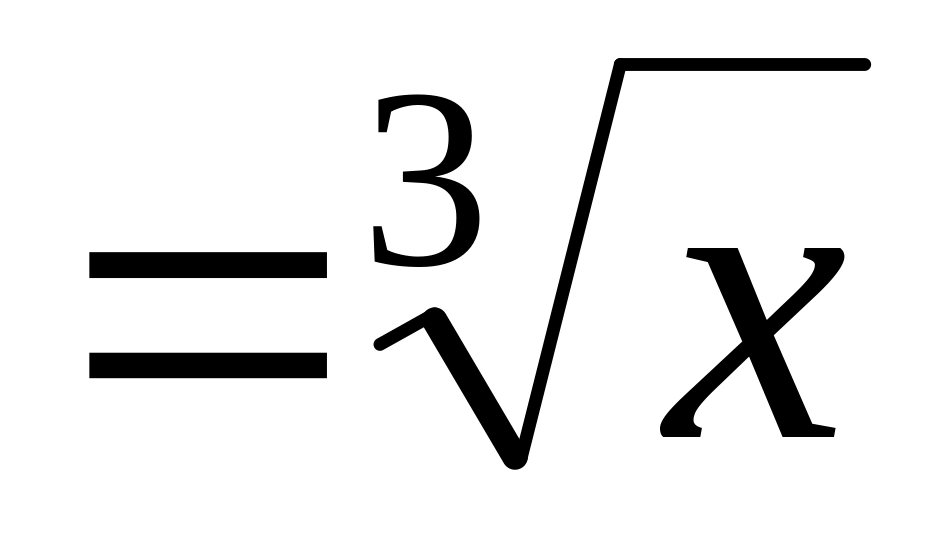 первообразная
первообразная
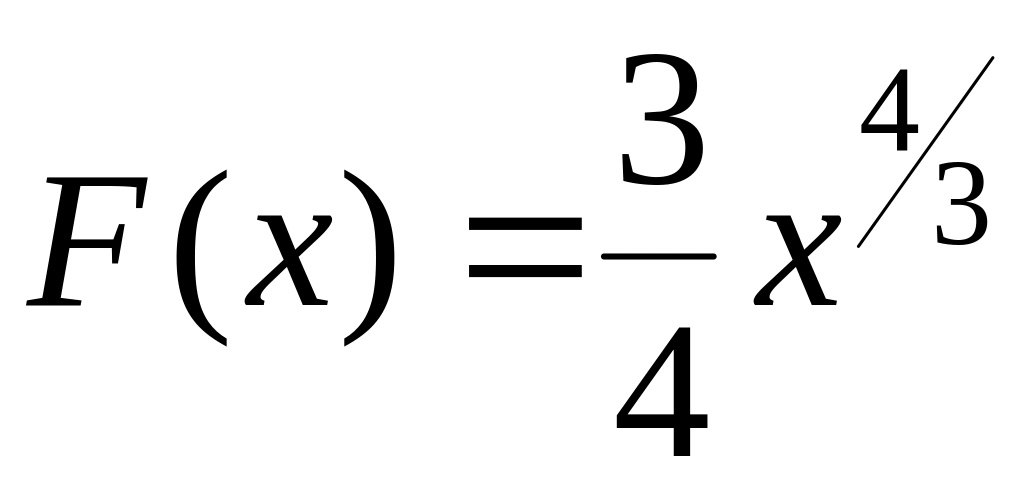 .
По формуле Ньютона-Лейбница находим
.
По формуле Ньютона-Лейбница находим
=![]() .
.
Для функции
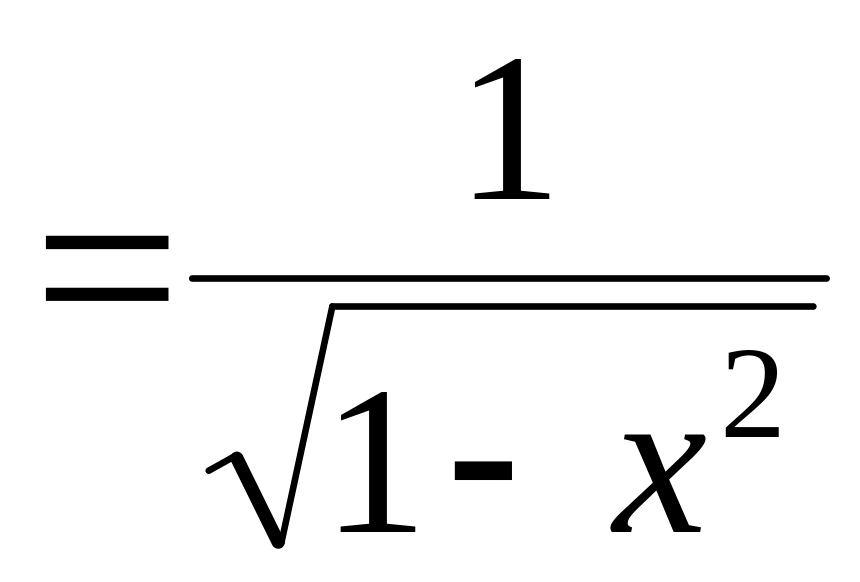 первообразная
первообразная
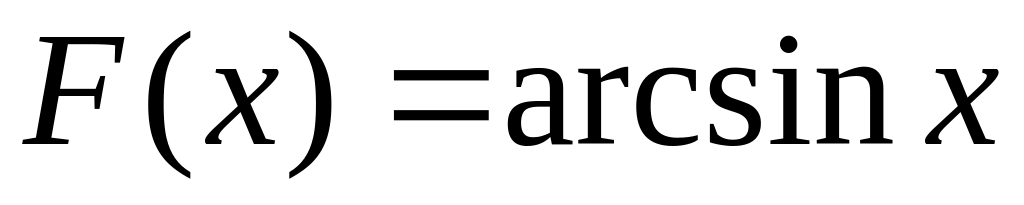 .
По формуле (1):
.
По формуле (1):
![]() .
.
Для
функции
![]() первообразная
первообразная
![]() .
По формуле (1):
.
По формуле (1):
 .
.
Пример 2. Вычислить интегралы
a) ,
b)
,
b)![]() ,
c)
,
c)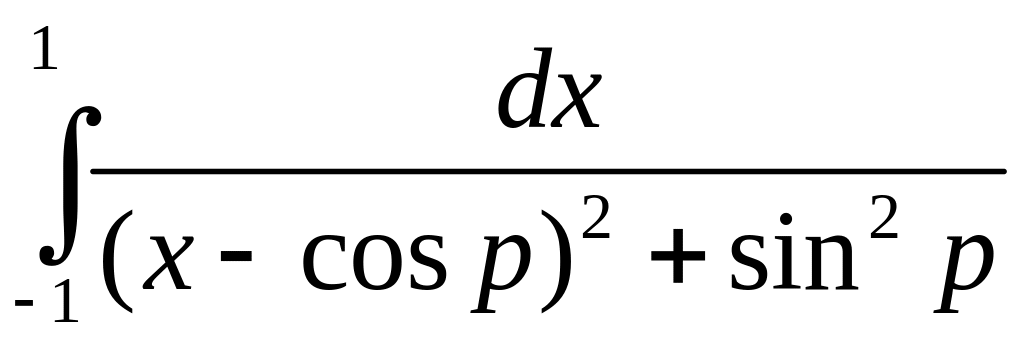 ,
,
![]() .
.
a) Для вычисления
первообразной применим стандартный
прием понижения степени: .
.
b) Так как подынтегральная
функция
![]() ,
то следует взять
,
то следует взять
![]() на промежутке интегрирования от
на промежутке интегрирования от
![]() до
до
![]() и
и
![]() на промежутке от
до
на промежутке от
до
![]() .
В силу аддитивности определенного
интеграла
.
В силу аддитивности определенного
интеграла
![]() ,
поэтому
,
поэтому
![]()
![]() .
.
c) Вычисление первообразной
сводится к табличному интегралу
![]() :
=
:
=![]()
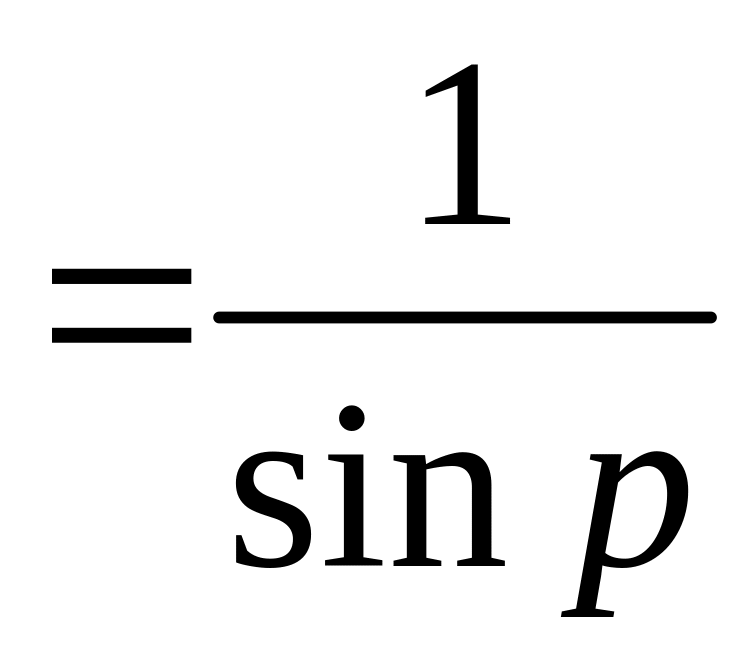
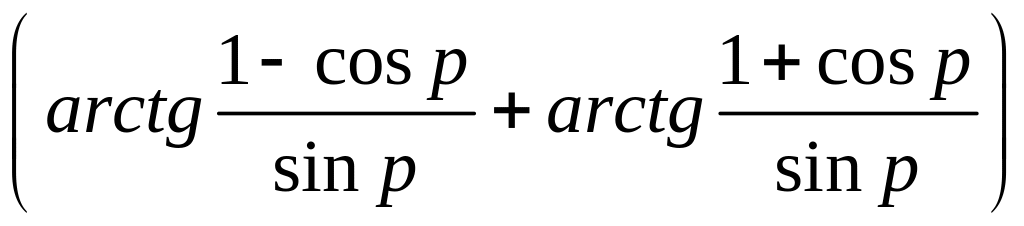 =
=![]()
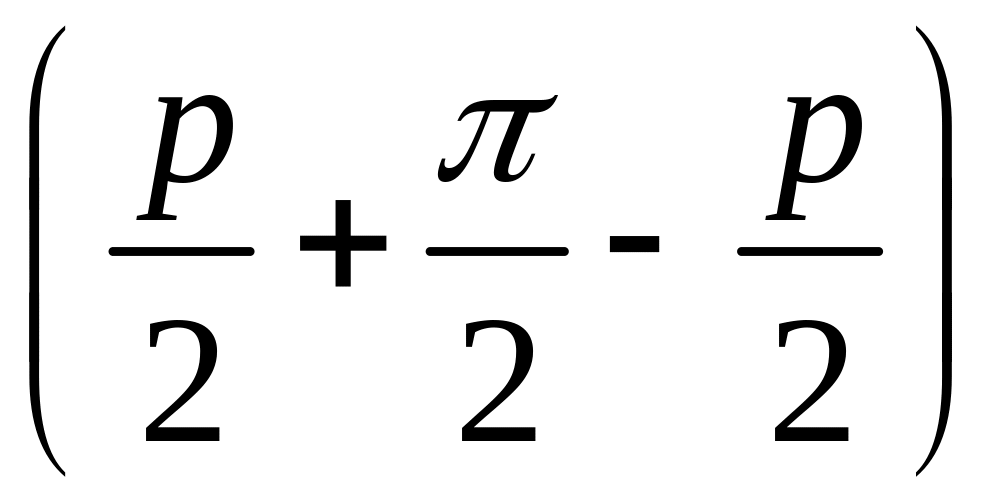 =
=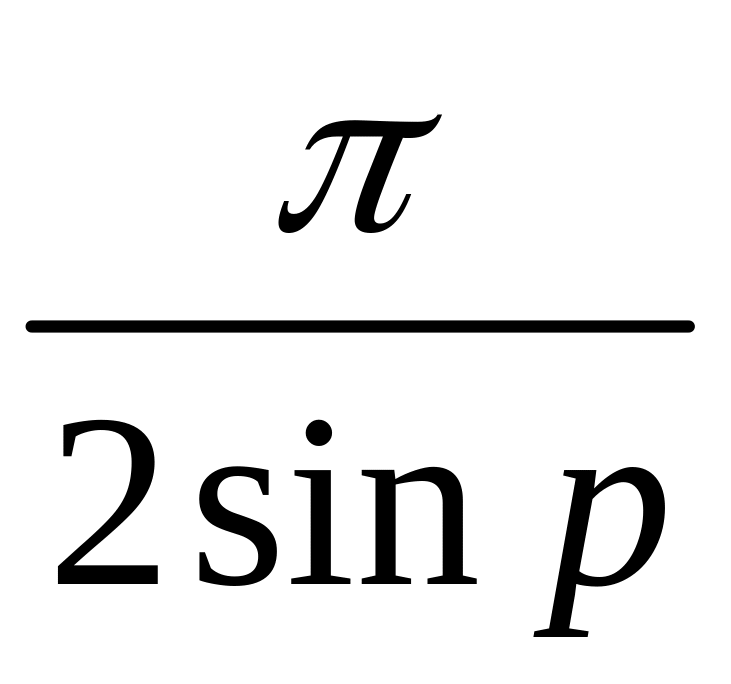 .
.
b) Интегрирование
по частям. Пусть функции
![]() и
и
![]() непрерывны вместе со своими производными
на отрезке
,
тогда
непрерывны вместе со своими производными
на отрезке
,
тогда
![]()

Или 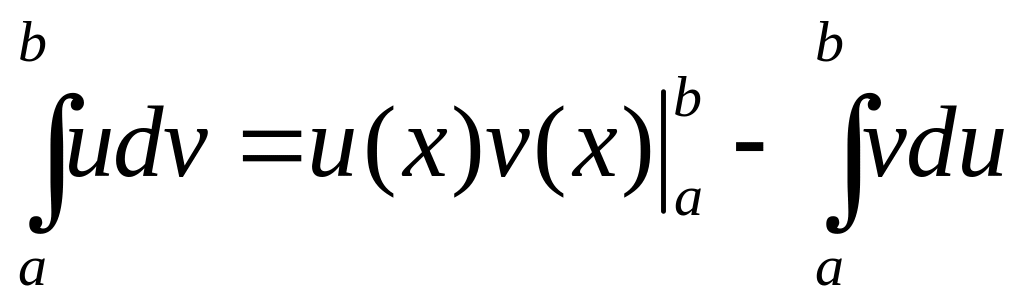 . (2)
. (2)
Пример 3. Вычислить интегралы
a)
![]() ,
b)
,
b)
![]() ,
c)
,
c)
![]() .
.
a) Стандартный для такого интеграла выбор частей и формула (2) приводят к результату:
![]() .
.
b)
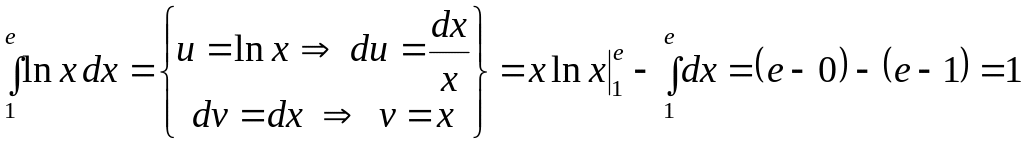 .
.
c)
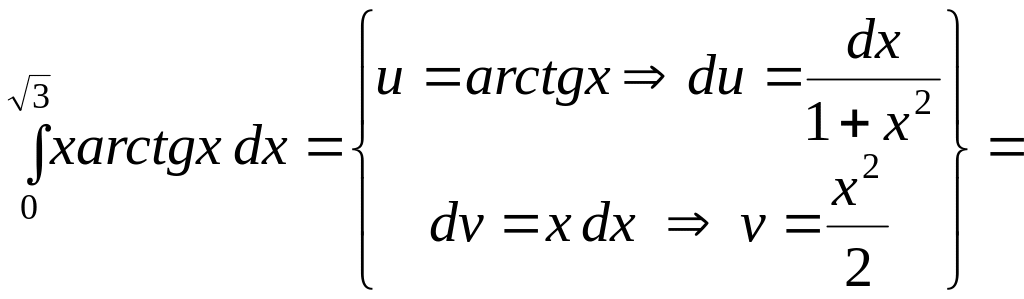
![]()
![]()
 .
.
c) Замена переменной. Пусть выполняются условия:
a) функция непрерывна на ;
b) функция
![]()
![]() непрерывна вместе со своей производной
непрерывна вместе со своей производной
![]() на
на
![]() ,
причем
,
причем
![]() и
и
![]() ;
;
с) сложная функция
![]() определена и непрерывна на
,
определена и непрерывна на
,
тогда
![]() . (3)
. (3)
Пример 4. Вычислить интегралы
a)![]() ;
b)
;
b)![]() ;
c)
;
c) ;
d)
;
d)![]() .
.
а) Как и при вычислении неопределенного
интеграла, здесь следует рационализировать
подынтегральное выражение. Для этого
выполним замену переменной
![]() ,
тогда
,
тогда
![]() .
Но сейчас следует найти пределы изменения
новой переменной
.
Но сейчас следует найти пределы изменения
новой переменной
![]() :
:
если
![]() ,
то
,
то
![]() ,
если
,
если
![]() ,
то
,
то
![]() .
.
В соответствии с формулой (3) получаем
![]()
![]()
![]() .
.
b) Не стоит возводить
двучлен в 12-ую степень и затем интегрировать
полином 25—го порядка. Замечая, что
![]() ,
выполним замену
,
выполним замену
![]() ,
тогда подынтегральное выражение
преобразуется к виду
,
тогда подынтегральное выражение
преобразуется к виду
![]() .
При изменении
от
до
новая переменная
изменяется от
до
.
.
При изменении
от
до
новая переменная
изменяется от
до
.
По формуле (3) запишем:
![]() .
.
Здесь учтено свойство определенного интеграла:
![]() .
.
с) Выполним замену переменной
![]() ,
тогда
,
тогда
![]() .
Найдем пределы изменения новой переменной
:
.
Найдем пределы изменения новой переменной
:
если
![]() ,
то
,
то
![]() ,
если
,
если
![]() ,
то
,
то
![]() .
.
При этом подынтегральное выражение преобразуется к виду
![]()
![]() .
.
Здесь учтено, что
![]() при
при
![]() ,
поэтому
,
поэтому
![]() .
.
По формуле (3) найдем
= =
=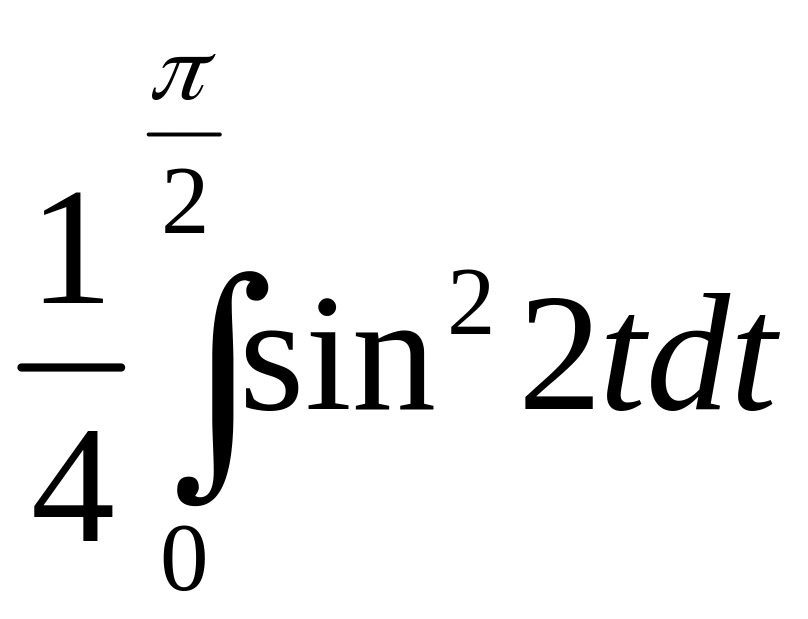 =
=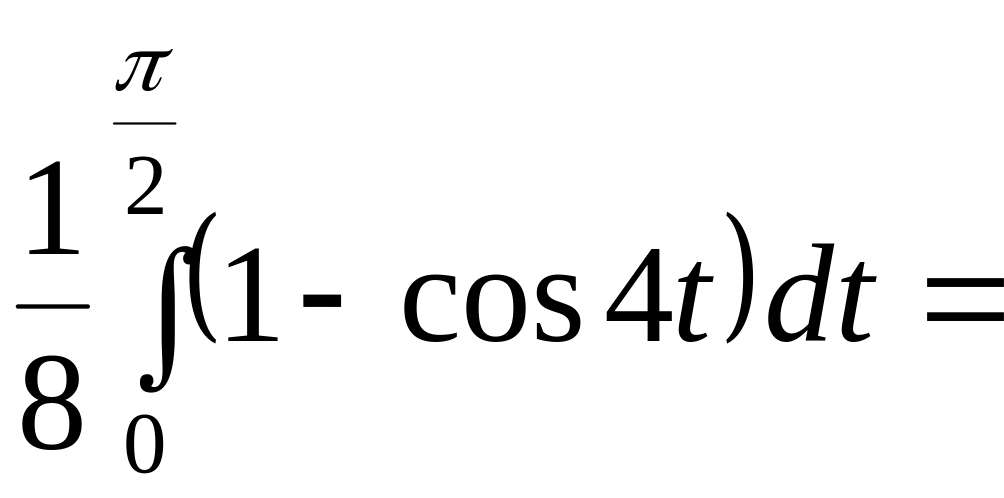
![]() .
.
d) Выполним замену переменной
![]() ,
тогда
,
тогда
![]() .
.
Найдем пределы изменения новой переменной :
если
,
то
![]() ,
,
если
![]() ,
то
,
то
![]() .
По формуле (3) получаем:
.
По формуле (3) получаем:
![]() .
.
Задание для самоcтоятельной работы
Вычислить интегралы и сравнить ответы с приведенными
1.
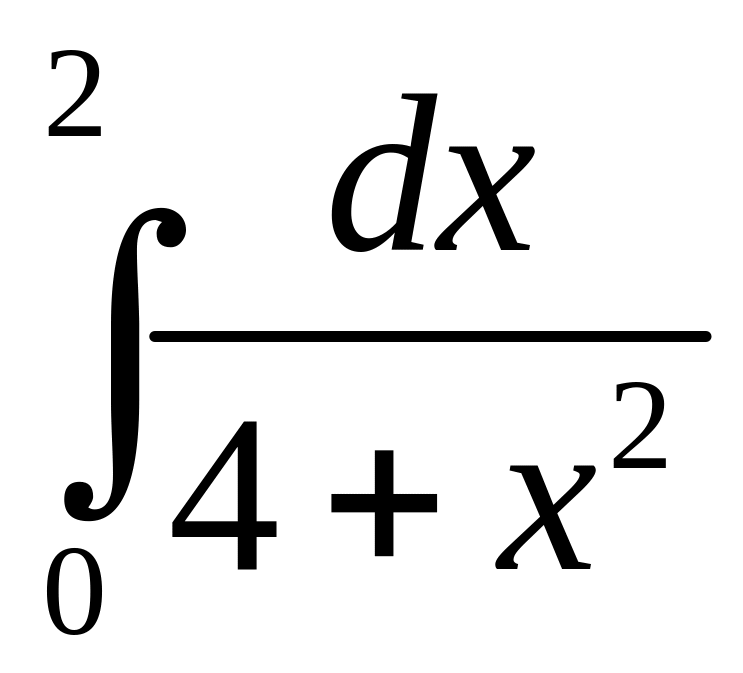 ;
2.
;
2.
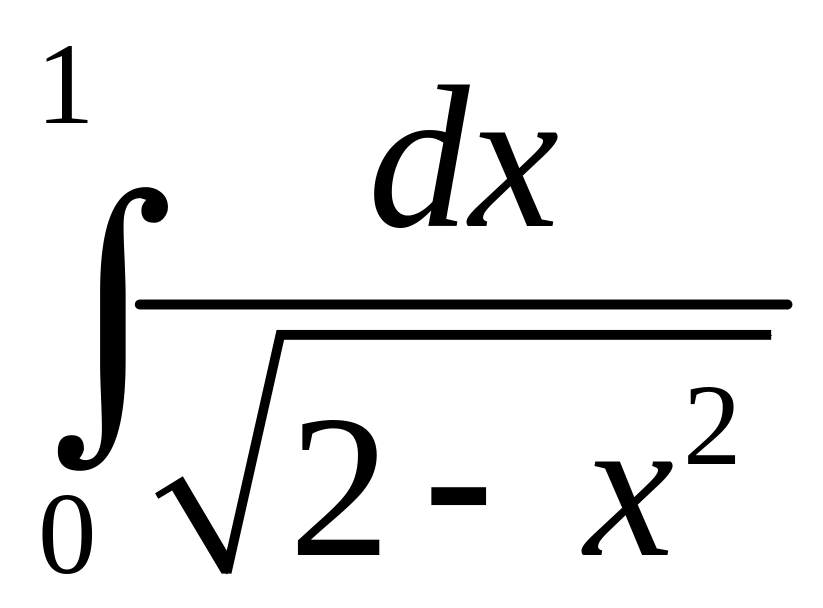 ;
3.
;
3.
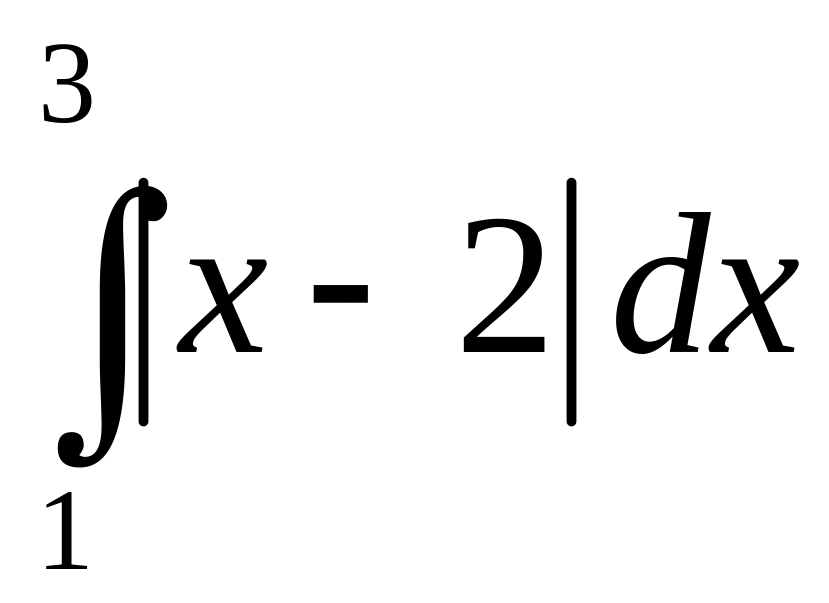 ;
;
4.
![]() ;
5.
;
5.
![]() ;
;
6.
![]() =
=![]() ;
7.
;
7.
![]() ;
;
8.
![]() ;
9.
;
9.
 =
=![]() ;
;
10.
![]() ;
11.
;
11.
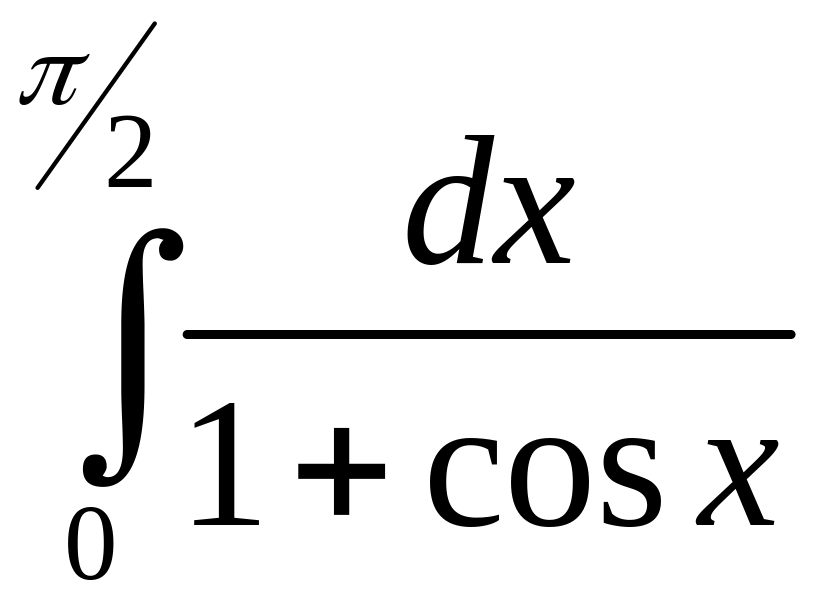 ;
;
12.
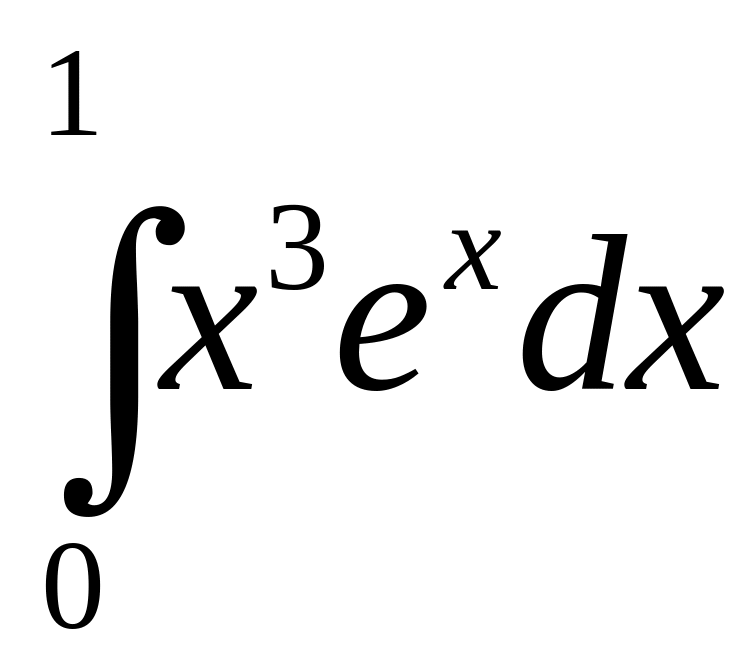 ;
13.
;
13.
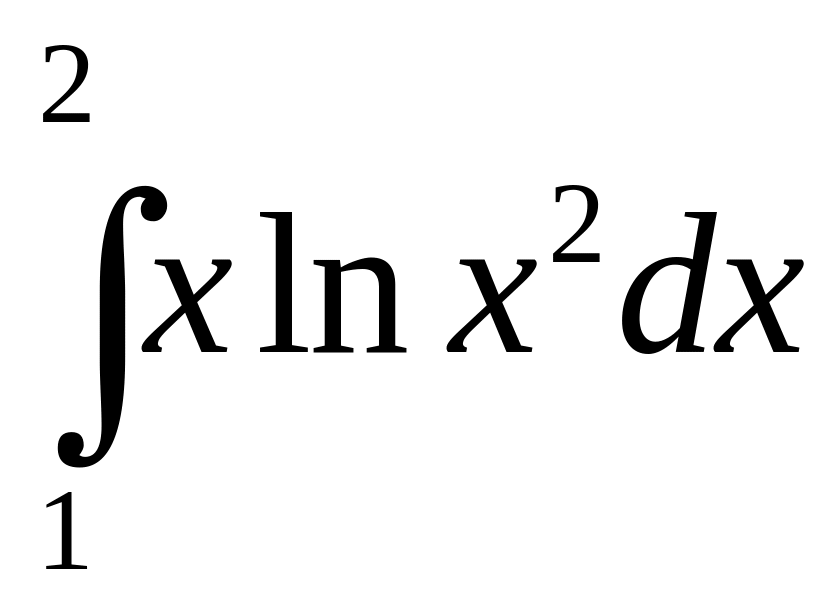 .
.
