Оглавление

1.Определенный интеграл. Критерий интегрируемости 1

2. Понятие определенного интеграла 2

а) Вычисление площади криволинейной трапеции 2

b) Вычисление пути по заданной скорости 3

3. Определение определенного интеграла 4

4. Ограниченность интегрируемой функции 5

5. Суммы Дарбу и их свойства 6

6. Необходимое и достаточное условие интегрируемости 8

7. Вычисление определенных интегралов 8

а) Формула Ньютона-Лейбница 8

b) Интегрирование по частям 10

c) Замена переменной 11

8. Длина дуги 13

а) Декартовы координаты 13

b) Параметрическое задание кривой 14

c) Полярные координаты 15

9. Площадь плоской фигуры 17

а) Декартовы координаты 17

b) Параметрическое задание кривой 20

c) Полярные координаты 21

10. Вычисление объемов 23

a) Объём ступенчатой фигуры 23

b) Объём тела вращении 25

11. Механические и физические задачи 29

1. Определенный интеграл. Критерий интегрируемости

Интеграл (от латинского слова integer- целый), одно из важнейших понятий математики. Возникновение интегрального исчисления связано с нахождением площадей и объемов. Ряд задач такого рода был решен математиками Древней Греции. Большую роль при решении таких задач играл исчерпывающий метод, созданный Евдоксом Книдским и широко применявшийся Архимедом. Однако Архимед не выделил общего содержания интеграционных приемов. Лишь в 16 и 17 веках развитие естественных наук поставило перед математикой ряд новых задач, в частности задачи на нахождения квадратур, кубатур и определение центров тяжести. Античный метод был возрожден И. Кеплером. В более общей форме эти методы были развиты Б. Кавальери, Э. Торричелли, Дж. Валлисом, Б. Паскалем.

В итоге этих исследований выявилась общность приемов интегрирования при решении внешне несходных задач геометрии и механики. Заключительным звеном в цепи открытий этого периода было установление обратной связи между дифференцированием и интегрированием. Основные понятия и алгоритм интегрального исчисления были созданы независимо друг от друга И.Ньютоном и Г.Лейбницем. Последнему принадлежит термин “интегральное исчисление” и обозначение интеграла . При этом в работах Ньютона основную роль играло понятие неопределенного интеграла, тогда как Лейбниц исходил из понятия определенного интеграла. В конце 19 − начале 20 века развитие теории множеств и теории функций привело к углублению и обобщению понятия интеграла благодаря работам О.Коши, Б.Римана, А.Лебега. С помощью интегрального исчисления стало возможным решать единым методом многие теоретические и прикладные задачи.

Чтобы подойти к понятию определенного интеграла, рассмотрим некоторые геометрические и физические задачи.

2. Понятие определенного интеграла

a) Вычисление площади криволинейной трапеции

Зададим на отрезке ( и – конечные числа) неотрицательную непрерывную функцию . Поставим задачу: требуется разумно определить понятие площади криволинейной трапеции – фигуры, ограниченной кривой , осью , прямыми и , и вычислить эту площадь. Поставленную задачу естественно решать так.

Произведем разбиение отрезка на частей точками

, (1)

выберем на каждом из частичных отрезков по произвольной точке , определим значение функции в каждой из этих точек и составим сумму

,

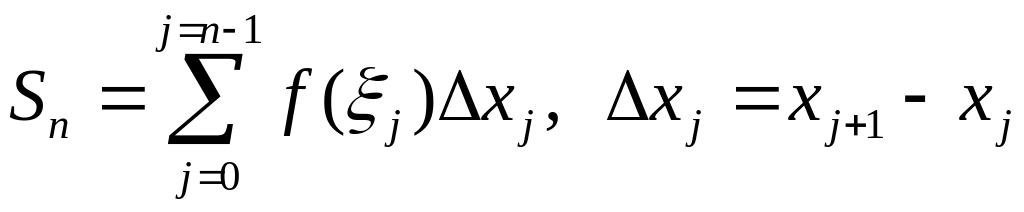которую называют интегральной суммой и которая, очевидно, равна сумме площадей затушеванных прямоугольников (см. рис.).

Будем теперь стремить все к нулю и притом так, чтобы максимальный (самый большой) частичный отрезок разбиения стремился к нулю. Если при этом величина стремится к определенному пределу , не зависящему ни от способа разбиения, ни от выбора точек на частичных отрезках, то естественно величину называть площадью криволинейной трапеции. Таким образом,

Итак, мы дали определение площади криволинейной фигуры. Возникает вопрос, имеет ли каждая такая фигура площадь, иначе говоря, стремится ли на самом деле к конечному пределу соответствующая интегральная сумма , когда ?

b) Вычисление пути по заданной скорости.

Пусть аргумент – время, а функция – скорость движения материальной точки по оси . Требуется вычислить путь, пройденный материальной точкой за время от до . Для решения этой задачи разобьем рассматриваемый промежуток времени на частичные промежутки точками

.

Будем считать, что на каждом частичном промежутке от до скорость меняется мало. Поэтому на каждом промежутке будем приближенно эту скорость полагать постоянной и равной, например, , где – произвольная точка промежутка . В таком случае путь, пройденный материальной точкой за время , приближенно равен . Путь, пройденный за весь промежуток времени, приближенно равен

.

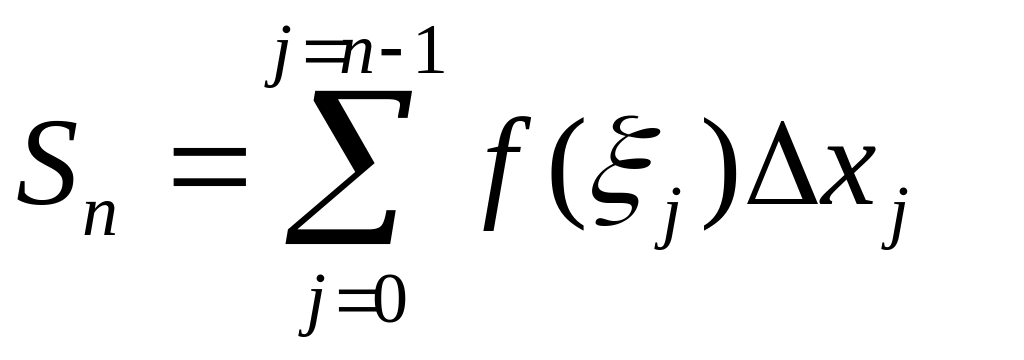Естественно ожидать, что при уменьшении всех промежутков времени мы будем получать все более и более точное значение пути. Чтобы получить точное значение пути необходимо в указанной сумме совершить предельный переход при .

Таким образом, две важные задачи: геометрическая задача о вычислении площади криволинейной трапеции и физическая задача о вычислении пути привели к одной и той же проблеме. Необходимо вычислить

При этом вопрос о том, что мы понимаем под пределом написанной суммы, конечно, требует выяснения.

Непосредственное вычисление предела интегральных сумм связано с трудностями: интегральные суммы сколько-нибудь сложных функций имеют громоздкий вид и зачастую не легко преобразовывать их к виду, удобному для вычисления пределов. Во всяком случае, на этом пути не удалось создать общих методов. Интересно отметить, что впервые задачу такого рода решил Архимед. При помощи рассуждений, которые отдаленно напоминают современный метод пределов, он вычислил площадь сегмента параболы. В дальнейшем на протяжении веков многие математики решали задачи на вычисление площадей фигур и объемов тел. Все же еще в 18 веке постановка таких задач и методы их решения носили сугубо частный характер. Существенный сдвиг в этом вопросе внесли Ньютон и Лейб-ниц, указавшие общий метод решения таких задач.