3.4.Определение доверительных интервалов.

Ранее мы получали оценки, которые являются точечными и не являются абсолютно точечными. Истинное значение может быть как меньше так и больше точечных оценок.

Поэтому правильнее было бы узнать интервал, в пределах которого заключено истинное значение. Совершенно очевидно, что как бы широк этот интервал не был (в разумных пределах) утверждать со 100% вероятностью, что истинное значение заключается в нем утверждать нельзя. Можно говорить об этом с той или иной долей вероятности.

Например: с вероятность 0,9 можно утверждать, что продолжительность жизни человека находится в интервале между 65 и 75 годами, а с вероятностью 0,99 между 50 и 80 годами

Рассмотрим способы определения доверительных интервалов и критерий доверия, то есть вероятность того, что рассмотренный параметры заключен в указанных параметрах.

Если из совокупности N взять несколько выборок. n₁,n₂,…n_k, и для каждой выборки определить Т_ср1,Т_ср2,…Т_срк, то все они будут разными.

Причем отклонения от Т_ср будут распределены нормальным законом.

Параметры закона по статистической совокупности определяется по следующим формулам.

n Тср*=∑ ti/n i=1

(3.20)

n S* =√∑(ti-Tcp) / n-1 i=1

(3.31)

где

S^* несмешанная оценка

n

Стандартное отклонение σ = √ ∑(t_i-T_cp)² / n

i=1

Получаемое значение из ряда выработок:

σ (Тср) = σ*/√n

(3.32)

где

n число отказов

Приведенные выражения позволяют непосредственно определить доверительный интервал. Для этого необходимо знать Т_ср и σ.

При числе отказов от 20-30 принять что Т_ср = Т_ср^*, σ = S^*

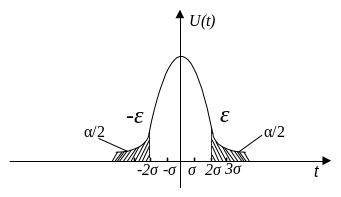
Если мы зададимся доверительной вертикалью, то есть площадью под кривой, то можем определить доверительный интервал. И наоборот, задавшись шириной интервала, можно определить коэффициент доверия.

Установлено, что доверительной интервал будет минимальный, если площадь под кривой плотности распределения U(t) в интервале (-∞ ; -2σ ][2σ ;+∞) будет равны

И если обозначить максимальное отклонение через Е то ширина интервала будет равна Т_ср± ε, а критерий доверия Р(Т_ср – ε ≤Т_ср≤ Т_ср+ε) =1-α

Р(Тср – ε ≤Тср≤ Тср+ε) =1-α

(3.23)

Вычисления критерия доверия, то есть вероятность взятой по обычной методике(по таблице интервала вероятности или функции Лапласа)

γ=1-σ = 2Фо [ε/ γ(Тср)] = 2Фо [(ε √n)/σ *] = 2Фо[(ε √n)/S*] =2Фо(Z)

(3.24)