
Добавил:
Yanus
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Все лекции / Тема 3 Динамика вращ. дв-я.ppt
X
- •Мультимедийные лекции по физике
- •Тема 3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
- •3.1. Момент инерции
- •Любое твёрдое тело состоит из множества материальных точек.
- •Момент инерции твёрдого тела
- •Для твёрдых тел неправильной геометрической формы массу тела разбивают на элементарные массы Δmi
- •Элементарные массы можно представить как
- •Момент инерции однородного цилиндра
- •Разобьем цилиндр на элементарные цилиндрические слои массой dm, расположенные в элементарных объемах dV.
- •Поскольку цилиндр однороден, то плотность тела
- •Учтем, что масса цилиндра
- •Моменты инерции тел правильной
- •Толстостенный цилиндр:
- •Теорема Штейнера
- •Пример: момент инерции шара относительно оси АВ.
- •Таким образом, момент инерции тела зависит от его формы, размеров, плотности, расположения оси
- •3.2. Момент силы
- •Момент силы относительно точки
- •Рисунок показывает взаимное расположение векторов, если смотреть вдоль вектора момента силы.
- •Здесь и на последующих рисунках значком обозначено направление вектора момента силы –
- •На рисунке показаны плечи сил.
- •Момент силы относительно оси
- •Моментом силы относительно некоторой оси Z называется проекция момента силы относительно любой точки,
- •Модуль момента силы относительно оси может быть положительным или отрицательным в зависимости от
- •Закреплённая ось вращения F
- •В случае закреплённой оси момент силы F относительно произвольной точки О равен сумме
- •При этом момент силы относительно закреплённой оси
- •Показано вращение материальной точки (элементарной массы) в плоскости.
- •Момент пары сил
- •Момент пары сил относительно некоторой точки О равен сумме моментов сил, образующих пару.
- •Пусть составляющие пару равные силы
- •Отсюда следует очень важный вывод о том, что сумма моментов всех внутренних сил
- •3.3. Момент импульса
- •Рассмотрим два часто встречающихся на практике случая движения материальной точки:
- •2. Движение материальной точки по окружности.
- •Момент импульса материальной точки
- •Модуль момента импульса относительно оси Z можно записать как
- •Момент импульса твердого тела относительно оси вращения
- •Выберем на оси Z произвольную точку О. Разобьем тело на материальные точки.
- •Момент импульса этой материальной точки относительно точки О равен:
- •Момент импульса всего тела относительно точки О равен векторной сумме моментов импульсов всех
- •Момент импульса твёрдого тела относительно закреплённой оси
- •Момент импульса твёрдого тела относительно оси равен скалярной сумме моментов импульсов всех точек
- •Тогда выражение для момента импульса тела
- •3.4. Основной закон динамики вращательного движения
- •Вычислим производную от вектора момента импульса
- •Подобное утверждение справедливо и для момента импульса материальной точки относительно некоторой оси Z.
- •Запишем такие же выражения для каждой точки вращающегося тела, а затем просуммируем по
- •Момент инерции J абсолютно твердого тела – постоянная величина.
- •J εz Mz внеш.
- •Графическая интерпретация
- •Условия равновесия твёрдого тела
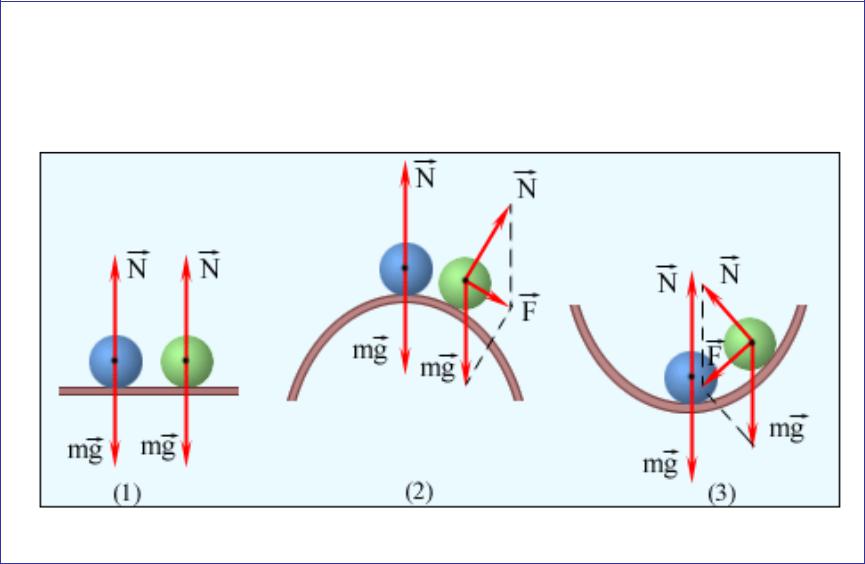
- •Равновесие может быть устойчивым (3), неустойчивым (метастабильным) (2) и безразличным (1).
- •1)- устойчивое положение равновесия;

Условия равновесия твёрдого тела
Из законов динамики поступательного и вращательного движений следуют условия равновесия тел.
Тело находится в покое (не движется поступательно и не вращается), если результирующая внешних сил равна нулю (первое условие равновесия) и результирующий момент внешних сил равен нулю (второе условие равновесия).
|
|
|
|
N |
|
N |
|
Fi 0, |
Mi 0. |
||
i 1 |
|
i 1 |
|
Равновесие может быть устойчивым (3), неустойчивым (метастабильным) (2) и безразличным (1).
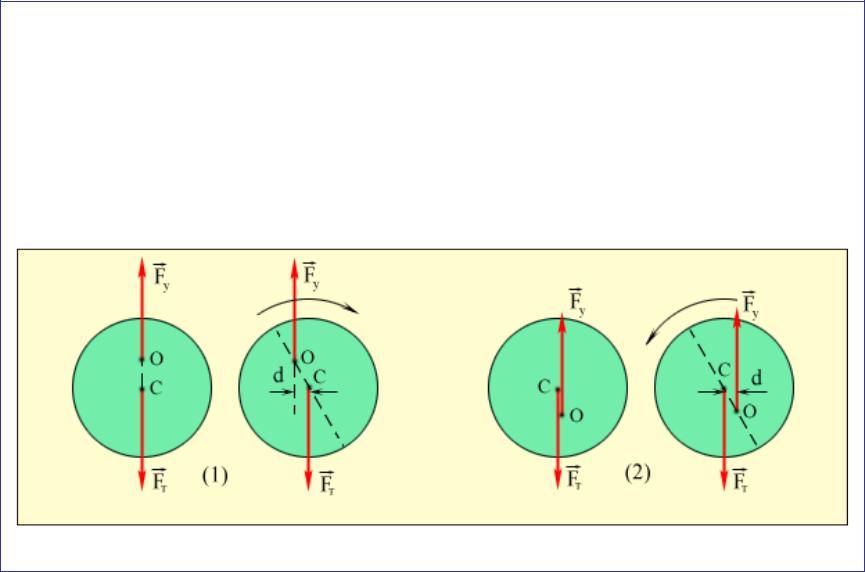
1)- устойчивое положение равновесия;
2)- неустойчивое положение равновесия.
В первом случае точки приложения сил находятся на прямой, проходящей через центр тяжести, во втором случае – в разных точках.
Соседние файлы в папке Все лекции
