Глава 22. Двойственность в линейном программировании

Произвольную задачу линейного программирования можно определенным образом сопоставить с другой задачей линейного программирования, называемой двойственной. Первоначальная задача является исходной. Эти две задачи тесно связаны между собой и образуют единую двойственную пару.

Различают симметричные, несимметричные и смешанные двойственные задачи.

22.1. Виды двойственных задач и составление их математических моделей

Симметричные двойственные задачи

Дана исходная задача

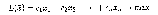
при ограничениях:

Задача дана в неканоническом виде. Составим математическую модель двойственной задачи, для этого:

• каждому неравенству системы ограничений исходной задачи приводим в соответствие переменную y_i;

• составляем целевую функцию, коэффициентами которой являются свободные члены системы ограничений исходной задачи;

• составляем систему ограничений. Коэффициенты системы ограничений образуют транспонированную матрицу коэффициентов системы ограничений исходной задачи. Знаки неравенств меняются на противоположные;

• свободными членами системы ограничений являются коэффициенты целевой функции исходной задачи. Все переменные двойственной задачи неотрицательные.

Математическая модель двойственной задачи имеет вид

при ограничениях:

Несимметричные двойственные задачи

Дана исходная задача

при ограничениях:

Задача дана в каноническом виде. Составим математическую модель двойственной задачи.

Для ее составления пользуются тем же правилом, что и для составления симметричной задачи, с учетом следующих особенностей:

• ограничениями двойственной задачи будут неравенства. Если в целевой функции двойственной задачи требуется найти минимум, то знак неравенства ≥, если максимум, то ≤;

• переменные y_i — произвольные по знаку.

Математическая модель двойственной задачи имеет вид

при ограничениях:

Смешанные двойственные задачи

Математическая модель исходной задачи имеет условия симметричных и несимметричных задач. При составлении двойственной задачи необходимо выполнять правила симметричных и несимметричных задач.

22.2. Основные теоремы двойственности

ТЕОРЕМА 1. Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений и выполняется равенство

Если одна из двойственных задач неразрешима ввиду того, что L( )_max → (или S( )_min → - ), тo другая задача не имеет допустимых решений.

ТЕОРЕМА 2. Для оптимальности допустимых решений и пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений

Теоремы позволяют определить оптимальное решение одной из пары задач по решению другой.

22.3. Решение двойственных задач

Решение симметричных задач

Рассмотрим решение задач с использованием теорем двойственности.

Решим исходную задачу графическим методом, получим _опт = (4, 1), при этом L( )_mах = 3.

На основании 1-й теоремы двойственности

Так как x₁, х₂ > 0, то по 2-й теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств:

Подставим _опт в систему ограничений исходной задачи:

Тогда система ограничений двойственной задачи примет вид

Откуда _опт = (0, 2/3, 1/3), при этом S( )_min = 3.

Пусть дано решение двойственной задачи _опт = (0, 2/3, 1/3), S( )_min = 3, найдем решение исходной.

По 1-й теореме двойственности L( )_max = S( )_min = 3. Так как у₂, y₃ > 0, то по 2-й теореме двойственности второе и третье неравенства исходной задачи обращаются в равенства:

Откуда _опт = (4,1), при этом L( )_mах = 3.

Рассмотрим решение задач методом, основанным на взаимно однозначном соответствии между переменными: основным переменным исходной задачи соответствуют балансовые переменные двойственной, и наоборот. Для этого решим двойственную задачу симплексным методом:

при ограничениях:

Из табл. 22.1 следует, что _опт = (0, 2/3, 1/3), S( )_min = 3.

На основании 1-й теоремы двойственности получаем

Решение другой задачи найдем по соответствию между переменными:

Значение x_j определяем по последней симплексной таблице в строке Δ_i в соответствующем столбце, причем значения x_j берем по модулю:

Таким образом, решение исходной задачи:

Если исходная задача решена симплексным методом, то решение двойственной задачи может быть найдено по формуле

где С — матрица-строка коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи; А^-1 — обратная матрица для матрицы А, являющейся матрицей коэффициентов базисных переменных системы ограничений исходной задачи в оптимальном решении.

Решим симплексным методом исходную задачу вида

при ограничениях:

Из табл. 22.2 следует, что _опт = (4,1), L( )_max = 3. Матрицы записываются в виде

тогда

Таким образом, решение двойственной задачи следующее:

Решение несимметричных задач

Рассмотрим решение задач с использованием теорем двойственности.

Решив двойственную задачу графическим методом, получим

По 1-й теореме двойственности L( )_min = S( )_max = 33/2.

Подставим _опт в систему ограничений двойственной задачи:

Так как х₃ = х₄ = 0, то система ограничений исходной задачи примет вид

Решая данную систему, получим

Рассмотрим решение задач с использованием обратной матрицы.

Пусть решение исходной задачи

Решение двойственной задачи найдем по формуле

где

Таким образом, _oпт = (1/2, 2), при этом S( )_max = 33/2.

Решение смешанных двойственных задач

Смешанные двойственные задачи можно решать с использованием теорем двойственности.

Найдем оптимальное решение двойственной задачи:

По 1-й теореме двойственности

Так как х₁ > 0, x₃ > 0, то по 2-й теореме двойственности первое и третье ограничения двойственной задачи выполняются в виде равенств: