18.6. Некоторые элементы математической статистики

Задачи математической статистики

Первой задачей математической статистики является указание методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюдений. Вторая задача — это разработка методов анализа статистических данных: оценки неизвестных вероятности события, а также функции и параметров распределения; оценка зависимости случайной величины от других случайных величин; проверка статистических гипотез о виде и величинах параметров неизвестного распределения. Рассмотрим некоторые из этих вопросов.

Выборки

На практике сплошное исследование (каждого объекта из интересующей нас совокупности) проводят крайне редко. К тому же если эта совокупность содержит большое число объектов или исследование объекта требует нарушения его функционального стандарта, то сплошное исследование нереально. В таких случаях из всей совокупности случайно отбирают ограниченное число объектов и подвергают их исследованию.

Введем основные понятия, связанные с выборками. Генеральной совокупностью называется совокупность объектов, из которых производится выборка. Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов из генеральной совокупности. Число объектов в совокупности называется ее объемом.

Пример 1. Пусть из 2000 изделий отобрано для обследования 100 изделий. Тогда объем генеральной совокупности N = 2000, а объем выборки п = 100.

Выборку можно осуществлять двумя способами. Если после исследования объект из выборки возвращается в генеральную совокупность, то такая выборка называется повторной; если объект не возвращается в генеральную совокупность, то выборка называется бесповторной.

Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности.

Способы отбора

Различают два способа отбора: без расчленения генеральной совокупности на части и с расчленением. К первому относятся простые случайные отборы (либо повторный, либо бесповторный), когда объекты извлекают по одному из всей генеральной совокупности; такой отбор можно производить с использованием таблицы случайных чисел.

Второй способ отбора включает в себя следующие разновидности, соответствующие способам расчленения генеральной совокупности. Отбор, при котором объекты отбираются из каждой "типической" части генеральной совокупности, называется типическим. Например, отбор деталей из продукции каждого станка, а не из их общего количества является типическим. Если генеральную совокупность делят на число групп, равное объему выборки, с последующим отбором из каждой группы по одному объекту, то такой отбор называется механическим. Серийным называется отбор, при котором объекты отбираются не по одному, а сериями; этот способ используется, когда исследуемый признак имеет незначительные колебания в различных сериях.

На практике часто употребляется комбинирование указанных выше способов отбора. Например, генеральную совокупность разбивают на серии одинакового объема, затем случайным образом отбирают несколько серий и в завершение случайным извлечением отдельных объектов составляют выборку. Конкретная комбинация способов отбора объектов из генеральной совокупности определяется требованием репрезентативности выборки.

Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка объема п, в которой значение x₁ некоторого исследуемого признака Х наблюдалось п₁ раз, значение x₂ — п₂ раз, ..., значение x_k — n_k раз. Значения x_i называются вариантами, а их последовательность, записанная в возрастающем порядке,— вариационным рядом. Числа n_i называются частотами, а их отношения к объему выборки

— относительными частотами. При этом n_i = п. Модой М_o называется варианта, имеющая наибольшую частоту. Медианой т_е называется варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой. Если число вариант нечетно, т.е. k = 2l + 1, то m_e = x_l+1; если же число вариант четно (k = 2l), то т_е = (x_l + x_l+1)/2. Размахом варьирования называется разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:

Перечень вариант и соответствующих им частот называется статистическим распределением выборки. Здесь имеется аналогия с законом распределения случайной величины: в теории вероятностей — это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — это соответствие между наблюдаемыми вариантами и их частотами (относительными частотами). Нетрудно видеть, что сумма относительных частот равна единице: W_i = 1.

Пример 2. Выборка задана в виде распределения частот:

Найти распределение относительных частот и основные характеристики вариационного ряда.

Решение. Найдем объем выборки: п = 2 + 4 + 5 + 6 + 3 = 20. Относительные частоты соответственно равны W₁ = 2/20 = 0,1; W₂ = 4/20 = 0,2; W₃ = 5/20 = 0,25; W₄ = 6/20 = 0,3; W₅ = 3/20 = 0,15. Контроль: 0,1 + 0,2 + 0,25 + 0,3 + 0,15 = 1. Искомое распределение относительных частот имеет вид

Мода этого вариационного ряда равна 12. Число вариант в данном случае нечетно: k = 2 ∙ 2 + 1, поэтому медиана m_e = x₃ = 8. Размах варьирования, согласно формуле (18.48), R = 17 – 4 = 13.

Эмпирическая функция распределения

Пусть n_х — число наблюдений, при которых значение признака Х меньше х. При объеме выборки, равном п, относительная частота события Х < х равна n_x/n.

Определение 8. Функция

определяющая для каждого значения х относительную частоту события Х < х, называется эмпирической функцией распределения, или функцией распределения выборки.

В отличие от эмпирической функции распределения F*(x) выборки функция распределения F(x) генеральной совокупности называется теоретической функцией распределения. Различие между ними состоит в том, что функция F(x) определяет вероятность события Х < х, a F*(x) — относительную частоту этого события. Из теоретических результатов общей теории вероятностей (закон больших чисел) следует, что при больших п вероятность отличия этих функций друг от друга близка к единице:

Нетрудно видеть, что F*(x) обладает всеми свойствами F(x), что вытекает из ее определения (18.49):

1) значения F*(x) принадлежат отрезку [0, 1];

2) F*(x) является неубывающей функцией;

3) если х₁ — наименьшая варианта, то F*(x) = 0 при х ≤ х₁; если x_k — максимальная варианта, то F*(x) = 1 при x > x_k.

Сама же функция F*(x) служит для оценки теоретической функции распределения F(x) генеральной совокупности.

Пример 3. Построить эмпирическую функцию по заданному распределению выборки:

Решение. Находим объем выборки: п = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F*(x) = 0 при х ≤ 2. Значение Х < 4 (или x₁ = 2) наблюдалось 10 раз, значит, F*(x) = 10/50 = 0,2 при 2 < х < 4. Значения X < 6 (а именно x₁ = 2 и x₂ = 4) наблюдались 10 + 15 = 25 раз, значит, при 4 < х < 6 функция F*(x) = 25/50 = 0,5. Поскольку x = 6 — максимальная варианта, то F*(x) = 1 при х > 6. Напишем формулу искомой эмпирической функции:

График этой функции показан на рис. 18.8.

Полигон и гистограмма

Каждую пару значений (x_i, n_i) из распределения выборки можно трактовать как точку на координатной плоскости. Точно так же можно рассматривать и пары значений (х_i, W_i) относительного распределения выборки. Ломаная, отрезки которой соединяют точки (x_i, n_i), называется полигоном частот. Ломаная, соединяющая на координатной плоскости точки (x_i, W_i), называется полигоном относительных частот. На рис. 18.9 показан полигон относительных частот для распределения, приведенного в примере 2.

Для случая непрерывного признака Х удобно разбить интервал (x_min, x_max) его наблюдаемых значений на несколько частичных интервалов длиной h каждый и найти для каждого из этих интервалов сумму частот n_j, попавших в него. Ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотами n_j/h (плотность частоты), называется гистограммой частот. Геометрический смысл гистограммы: нетрудно видеть, что площадь ее равна сумме всех частот или объему выборки. На рис. 18.10 изображена гистограмма объема n = 100.

Аналогичным образом определяется и гистограмма относительных частот: в этом случае высоты прямоугольников, составляющих ступенчатую фигуру, определяются отношениями сумм относительных частот, попадающих в интервал (x_min + (j — 1)h, x_min + jh), к длине интервала h, т.е. величинами W_j/h. Нетрудно видеть, что площадь гистограммы относительных частот равна единице (сумме относительных частот выборки).

Статистические оценки параметров распределения

Значения количественного признака х₁, х₂, ..., х_k в выборке можно рассматривать как независимые случайные величины. В таком случае нахождение статистической оценки неизвестного параметра теоретического распределения означает отыскание функции от наблюдаемых случайных величин, которая и даст нам приближенное значение искомого параметра. Укажем виды статистических оценок.

Несмещенной называется статистическая оценка , математическое ожидание которой равно оцениваемому параметру при любой выборке:

Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки п. Состоятельной называется статистическая оценка типа (18.50), которая при п > стремится по вероятности к оцениваемому параметру.

Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности

и выборочная средняя

Если значения признака х₁, x₂, …, х_k в выборке имеют соответственно частоты n₁, n₂, ..., n_k, то последнюю формулу можно переписать в виде

Можно показать, что выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины.

Введем в рассмотрение величины, характеризующие отклонение значений количественного признака Х от своего среднего значения. Это генеральная дисперсия:

и выборочная дисперсия:

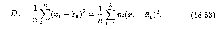
Можно показать, что для вычисления этих характеристик справедливы более удобные формулы, аналогичные дисперсии случайной величины; так, формула (18.53) принимает вид

Генеральное среднее квадратическое отклонение определяется как

Аналогично вводится и выборочное среднее квадратическое отклонение

Пример 4. Выборка задана таблицей распределения

Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.

Решение. По формуле (18.52) сначала находим _в:

Затем по формулам (18.54) и (18.55) находим две другие искомые величины:

Виды дисперсий

Часто значения количественного признака Х совокупности разбиваются на определенное число групп. Каждую группу можно рассматривать как самостоятельную выборку, и для каждой группы можно определить групповую среднюю и дисперсию. Пусть r — число групп. Групповой дисперсией на зывается дисперсия значений признака в группе относительно групповой средней:

где n_i — частота значения x_i в группе, j — номер группы _j — групповая средняя j-й группы, N_j = n_i, — объем j-й группы.

Зная дисперсию каждой группы, можно определить их среднюю арифметическую. Внутригрупповой дисперсией называется средняя арифметическая дисперсий, где каждое слагаемое входит с весом объема группы:

В свою очередь, зная для всех групп средние _j и общую среднюю , введем еще одно понятие. Межгрупповой дисперсией называется дисперсия групповых средних относительно общей средней:

где п = — объем всей совокупности.

Для общей дисперсии всей совокупности справедлива следующая теорема, которая приводится здесь без доказательства.

ТЕОРЕМА 6. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:

где слагаемые в правой части определяются соответственно формулами (18.57) и (18.58).

Поясним сказанное в этом пункте на примере.

Пример 5. Совокупность состоит из двух следующих групп:

Найти групповые, внутригрупповую, межгрупповую и общую дисперсии.

Решение. Объемы групп соответственно равны N₁ = 10 и N₂ = 5. Общий объем совокупности: п = 10 + 5 = 15. Найдем групповые средние:

Теперь находим групповые дисперсии по формуле (18.56):

Внутригрупповая дисперсия, согласно формуле (18.57), равна:

Теперь найдем межгрупповую дисперсию по формуле (18.58), для чего сначала определим общую среднюю:

Наконец, общая дисперсия, согласно формуле (18.59), равна:

Эмпирические моменты

Для вычисления сводных характеристик выборок используют эмпирические моменты, аналогичные соответствующим теоретическим моментам. Обычным эмпирическим моментом порядка s называется среднее значение s-x степеней разностей x_i — С, где x_i — наблюдаемая варианта, С — произвольная постоянная (ложный нуль — либо мода, либо любая варианта, расположенная примерно в середине вариационного ряда):

При C = 0 имеем начальные эмпирические моменты порядка s; в частности, в случае s = 1

Центральным эмпирическим моментом порядка s называется обычный момент (18.60) при С = _в:

В частности,

Иными словами, выборочная дисперсия равна центральному эмпирическому моменту второго порядка. Центральные моменты выражаются через обычные по формулам, полностью аналогичным (18.19) и (18.20).

Асимметрия и эксцесс эмпирического распределения

Нормальное распределение является одним из самых распространенных в применениях математической статистики. Для оценки отклонения эмпирического распределения от нормального используют характеристики, аналогичные для теоретического распределения (см. предыдущий раздел 18.6).

Асимметрия эмпирического распределения определяется следующим равенством:

Эксцесс эмпирического распределения определяется следующим равенством:

В формулы (18.62) и (18.63) входят центральные эмпирические моменты, определяемые формулами (18.61), а также выборочное среднее квадратическое отклонение (18.55).

Пример 6. Найти асимметрию и эксцесс эмпирического распределения:

Решение. Найдем сначала _в и σ_в с использованием формул (18.52)-(18.55):

Далее, используя формулы (18.61), определяем центральные эмпирические моменты третьего и четвертого порядков:

Затем по формулам (18.62) и (18.63) находим искомые величины:

В заключение отметим, что все оценки, приведенные выше, определяются одним числом, т.е. являются точечными. При малых объемах выборки точечная оценка может приводить к большим ошибкам и значительно отличаться от оцениваемого параметра.

УПРАЖНЕНИЯ

18.1. Из коробки с шестью деталями, среди которых четыре стандартные, наудачу взяты три детали. Составить закон распределения дискретной случайной величины Х — количества стандартных деталей среди отобранных.

18.2. Книга издана тиражом 100 тысяч экземпляров. Вероятность брака в книге равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг.

18.3. Случайная составляющая дохода равна 2Х, а случайная составляющая затрат равна 50Y. Найти дисперсию прибыли при условиях: величина Х распределена по биномиальному закону с параметрами п = 100, р = 0,5; величина Y распределена по закону Пуассона с параметром λ = 2; случайные величины Х и Y являются независимыми.

18.4. Найти дисперсию и среднее квадратическое отклонение случайной величины X, заданной законом распределения

18.5. Найти дисперсию дискретной случайной величины Х — числа отказов элемента некоторого устройства — в 10 независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9.

18.6. Дискретная случайная величина Х задана законом распределения

Найти центральные моменты первого, второго, третьего и четвертого порядков.

18.7. Дано распределение двумерной дискретной случайной величины (X, Y):

Найти ковариацию Cov (X, Y) и коэффициент корреляции Х и Y.

18.8. Непрерывная случайная величина Х задана на всей оси Ох функцией распределения F(x) = 1/2 + (arctg x) / π. Найти вероятность того, что величина Х примет значение, заключенное в интервале (0, 1).

18.9. Случайная величина Х задана функцией распределения

Найти вероятность того, что Х примет значения: а) менее 0,2; б) менее трех; в) не менее трех; г) не менее пяти.

18.10. Дискретная случайная величина задана законом распределения

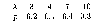
Найти функцию распределения и построить ее график.

18.11. Дана плотность распределения непрерывной случайной величины X:

Найти функцию распределения F(x).

18.12. Случайная величина Х задана на положительной полуоси Ох функцией распределения F(x) = 1 - e^-ax (а > 0). Найти математическое ожидание величины X.

18.13. Случайная величина Х задана на интервале (0,5) плотностью распределения f(x) = 2.x / 25; вне этого интервала f(x) = 0. Найти дисперсию X.

18.14. Случайная величина Х задана плотностью распределения f(x) = е^-|x| / 2. Найти математическое ожидание и дисперсию.

18.15. Случайная величина задана функцией распределения

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

18.16. Найти дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интервале (2, 8).

18.17. Ребро куба х измерено приближенно в интервале (а, b). Найти математическое ожидание и дисперсию объема куба, если его ребро рассматривать как случайную величину Х с равномерным распределением на указанном интервале.

18.18. Размер мужских сорочек является случайной величиной с нормальным законом распределения, математическим ожиданием 39 и дисперсией 9. Какой процент от общего объема заказа следует предусмотреть магазину для сорочек 40-го размера воротничка при условии, что этот размер находится в интервале (39,5; 40,5)?

18.19. Найти формулу плотности вероятности нормально распределенной случайной величины X, если математическое ожидание равно 3, а дисперсия равна 16.

18.20. Случайная величина Х распределена нормально с математическим ожиданием а = 25. Вероятность попадания Х в интервал (10, 15) равна 0,2. Найти вероятность попадания Х в интервал (35, 40).