15.5. Однородные системы линейных уравнений

Определение 1. Система линейных уравнений называется однородной, если во всех ее уравнениях свободные члены равны нулю.

В общем случае однородная система (или система однородных уравнений) имеет вид

Однородная система уравнений всегда совместна. Действительно, набор значений неизвестных x_i = 0 (i = 1, 2,... , п) удовлетворяет всем уравнениям системы. Это решение однородной системы называется нулевым, или тривиальным.

Решение системы однородных уравнений

Вопрос о существовании ненулевого решения однородной системы линейных уравнений (15.14) разрешает следующая теорема.

ТЕОРЕМА 3. Однородная система имеет ненулевое решение тогда и только тогда, когда ранг этой системы меньше числа ее неизвестных.

Из этой теоремы вытекают два важных следствия.

Следствие 1. Если число уравнений однородной системы меньше числа ее неизвестных, то эта система имеет ненулевое решение.

Следствие 2. Если в однородной системе число уравнений равно числу неизвестных, то она имеет ненулевое решение тогда и только тогда, когда определитель матрицы системы равен нулю.

Фундаментальная система решений

Решения однородной системы обладают следующими свойствами. Если вектор = (α₁, α₂,... ,α_n) является решением системы (15.14), то и для любого числа k вектор k = (kα₁, kα₂,..., kα_n) будет решением этой системы. Если решением системы (15.14) является вектор = (γ₁, γ₂, ... ,γ_n), то сумма + также будет решением этой системы. Отсюда следует, что любая линейная комбинация решений однородной системы также является решением этой системы.

Как мы знаем из п. 12.2, всякая система n-мерных векторов, состоящая более чем из п векторов, является линейно зависимой. Таким образом, из множества векторов-решений однородной системы (15.14) можно выбрать базис, т.е. любой вектор-решение данной системы будет линейной комбинацией векторов этого базиса. Любой такой базис называется фундаментальной системой решений однородной системы линейных уравнений. Справедлива следующая теорема, которую мы приводим без доказательства.

ТЕОРЕМА 4. Если ранг r системы однородных уравнений (15.14) меньше числа неизвестных п, то всякая фундаментальная система решений системы (15.14) состоит из п - r решений.

Укажем теперь способ нахождения фундаментальной системы решений (ФСР). Пусть система однородных уравнений (15.14) имеет ранг r < п. Тогда, как следует из правил Крамера, базисные неизвестные этой системы x₁, x₂, … x_r линейно выражаются через свободные переменные x_r+1, x_r+2 , ..., x_п:

Выделим частные решения однородной системы (15.14) по следующему принципу. Для нахождения первого вектора-решения ₁ положим x_r+1 = 1, x_r+2 = x_r+3 = ... = x_n = 0. Затем находим второе решение ₂: принимаем x_r+2 = 1, а остальные r - 1 свободных переменных положим нулями. Иными словами, мы последовательно присваиваем каждой свободной переменной единичное значение, положив остальные нулями. Таким образом, фундаментальная система решений в векторной форме с учетом первых r базисных переменных (15.15) имеет вид

ФСР (15.16) является одним из фундаментальных наборов решений однородной системы (15.14).

Пример 1. Найти решение и ФСР системы однородных уравнений

Решение. Будем решать эту систему методом Гаусса. Поскольку число уравнений системы меньше числа неизвестных, считаем х₁, x₂, х₃ базисными неизвестными, а x₄, х₅, x₆ — свободными переменными. Составим расширенную матрицу системы и выполним действия, составляющие прямой ход метода:

Преобразованная расширенная матрица соответствует системе уравнений, которая эквивалентна исходной однородной системе:

Обратный ход метода Гаусса дает значения базисных неизвестных, выраженные через свободные переменные:

Поскольку ранг однородной системы равен трем, то ФСР для нее состоит из трех линейно независимых векторов. По формулам (15.16) при п = 6 и r = 3, беря последовательно для свободных переменных тройки чисел (1, 0, 0), (0, 1, 0) и (0, 0, 1), получаем набор фундаментальных решений:

Характеристическое уравнение

В п. 13.1 было введено определение собственного значения и гобственного вектора матрицы. Пусть — собственный вектор квадратной матрицы А порядка n. Тогда имеет место матричное уравнение

или

где λ — собственное значение матрицы А, а E и — соответственно единичная матрица и нулевой вектор-столбец. Уравнение (15.17) эквивалентно системе однородных уравнений

В уравнениях (15.18) a_ij — элементы матрицы А, x_j — координаты собственного вектора х. Поскольку собственный вектор не является нулевым, то однородная система (15.18) должна иметь ненулевое решение, т.е. в силу следствия 2 (см. выше) определитель этой системы равен нулю:

Определитель системы однородных уравнений (15.18) называется характеристическим многочленом, а уравнение (15.19) — характеристическим уравнением матрицы А.

Уравнение (15.19) имеет степень n относительно неизвестной λ. Его корни являются собственными числами матрицы А. Определив набор этих чисел, для каждого из них можно найти соответствующий собственный вектор как решение однородной системы (15.18).

Пример 2. Найти собственные числа и собственные векторы матрицы

Решение. Характеристическое уравнение для этой матрицы имеет вид

откуда, раскрывая определитель, получаем

Корни этого уравнения суть λ₁ = 2, λ₂ = 5. Для нахождения собственных векторов подставим найденные собственные значения в систему однородных уравнений (15.18) при n = 2 с соответствующими элементами заданной матрицы А. Собственный вектор, соответствующий собственному значению λ₁ = 2, является решением системы

Пo сути дела, это одно уравнение, поскольку определитель системы равен нулю. Полагая x₂ = b свободной переменной, получаем первый собственный вектор ₁ = (—2b, b) = b (-2, 1). Подстановка второго собственного значения λ₂ = 5 приводит к системе уравнений

которая через свободную переменную x₂ = с определяет второй собственный вектор матрицы А: ₂ = (с, с) = с (1, 1).

Поскольку b и с — произвольные числа, то одному собственному значению может соответствовать несколько собственных векторов разной длины. Например, собственные векторы, соответствующие фундаментальным решениям однородных систем (в данном случае их будет по одному на каждое собственное значение), имеют вид ₁ = (-2, 1), ₂ = (1, 1).

УПРАЖНЕНИЯ

Решить методом Крамера системы линейных уравнений.

Решить системы линейных уравнений методом Гаусса.

Решить методом обратной матрицы системы уравнений, предварительно вычислив методом Гаусса обратную матрицу.

Найти фундаментальные системы решений однородных систем.

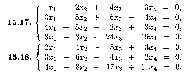
Найти собственные векторы и собственные значения матриц.