9.4. Линейные уравнения первого порядка

Определение 7. Уравнение вида

где р(х) и q(x) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Неизвестная функция и ее производная входят в указанное уравнение в первой степени — линейно, что и объясняет название уравнения.

Если q(x) 0, то уравнение (9.7) называется линейным однородным уравнением; если же функция q(x) не равна тождественно нулю, то уравнение (9.7) называется линейным неоднородным уравнением.

Для линейного уравнения первого порядка можно выписать общее решение с помощью метода вариации постоянной. Здесь это решение приводится без вывода:

Следует отметить, что некоторые нелинейные уравнения приводятся к линейным уравнениям соответствующими заменами неизвестной функции у(х). К таковым относится уравнение Бернулли

где р и q — непрерывные функции, a n — некоторое постоянное число. При п = 0 имеем линейное неоднородное уравнение, а при n = 1 — линейное однородное уравнение

Пусть п ≠ 0, n ≠ 1. Введем новую функцию

тогда

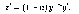
Поделим обе части уравнения (9.9) на уⁿ:

Умножая обе части этого уравнения на (1 — n), с учетом выражений для новой функции z и ее производной получаем линейное дифференциальное неоднородное уравнение относительно неизвестной функции z(x):

В этом уравнении, метод решения которого нам известен, функция z(x) связана с искомой функцией у(x) соотношением (9.10).

Рассмотрим примеры решения неоднородных уравнений первого порядка.

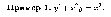
Решение. Это линейное неоднородное уравнение первого порядка. Последовательное интегрирование в формуле (9.8) при р(х) = x² и q(x) = х² дает

(этот интеграл берется с помощью подстановки t = х³ в формулу (9.8)). Получаем решение дифференциального уравнения:

Решение. Тот же прием, что и в предыдущем примере, при р(х) = 1/х и q(x) = e^х дает нам решение

Решение. Данное нелинейное уравнение представляет собой уравнение Бернулли при п = 3. Заменой искомой функции z = у^-2, согласно (9.10) и (9.11), получим линейное неоднородное уравнение относительно z(х)

По формуле (9.8) получаем общее решение этого уравнения:

Теперь, выполняя обратную замену у = ±1/ , получаем решение исходного нелинейного уравнения:

УПРАЖНЕНИЯ

Найти общие решения дифференциальных уравнений методом разделения переменных.

Найти частные решения уравнений первого порядка, удовлетворяющие указанным начальным условиям.

Найти общее решение линейных уравнений.

Решить уравнения Бернулли.

Глава 10. Дифференциальные уравнения второго порядка

10.1. Основные понятия теории

Определение 1. Дифференциальным уравнением второго порядка называется уравнение вида

где х — независимая переменная, у — искомая функция, у' и у" — соответственно ее первая и вторая производные.

Примеры дифференциальных уравнений второго порядка:

Будем рассматривать уравнения, которые можно записать в виде, разрешенном относительно второй производной:

Как и в случае уравнения первого порядка, решением уравнения (10.1) называется функция у = φ(x), определенная на некотором интервале (а, b), которая обращает это уравнение в тождество. График решения называется интегральной кривой. Имеет место теорема существования и единственности решения уравнения второго порядка.

ТЕОРЕМА 1 (теорема Коши). Пусть функция f(x, у, у') и ее частные производные и , непрерывны в некоторой области D пространства переменных (x, у, у'). Тогда для любой внутренней точки М₀(х₀, у₀, у'₀) этой области существует единственное решение уравнения (10.2), удовлетворяющее условиям:

Геометрический смысл этой теоремы (ее доказательство мы не приводим) заключается в том, что через заданную точку (x₀, y₀) на координатной плоскости Оху проходит единственная интегральная кривая с заданным угловым коэффициентом y₀' касательной (рис. 10.1).

Условия (10.3) называются начальными условиями, а задачу отыскания решения уравнения (10.2) по заданным начальным условиям называют задачей Коши.

Общим решением уравнения (10.2) в некоторой области D называется функция у = φ(х, С₁, С₂), если она является решением этого уравнения при любых постоянных величинах С₁ и C₂, которые могут быть определены единственным образом при заданных начальных условиях (10.3). Частным решением уравнения (10.2) называется общее решение этого уравнения при фиксированных значениях постоянных С₁ и C₂: у = φ(х, С₁⁰, С₂⁰).

Рассмотрим для пояснения уравнение у" = 0. Его общее решение получается при двухкратном интегрировании этого уравнения:

где С₁ и C₂ — произвольные постоянные. Это решение пред ставляет собой семейство прямых, проходящих в произвольных направлениях, причем через каждую точку плоскости Охy проходит бесконечное число таких прямых. Поэтому для выделения частного решения, проходящего через заданную точку (х₀, y₀), следует задать еще и угловой коэффициент прямой, совпадающей в данном случае со своей касательной. Например, найдем частное решение, удовлетворяющее начальным условиям

т.е. нужно найти прямую, проходящую через точку M (l, 2), с угловым коэффициентом, равным единице. Подстановка начальных условий в общее решение уравнения приводит к системе двух линейных уравнений относительно постоянных С₁ и C₂

откуда С₁ = 1, C₂ = 1. Таким образом, искомое частное решение — это прямая у = х + 1.