5.4. Применение в экономике

Предельные показатели в микроэкономике

Приведем примеры двух предельных показателей в микроэкономике.

1. Первый из них связан с зависимостью себестоимости С произведенной продукции от ее объема Q: С = f(Q). Так называемая предельная себестоимость характеризует себестоимость ΔC прироста продукции ΔQ:

В предположении о непрерывной зависимости ΔС от ΔQ естественно напрашивается замена разностного отношения в (5.13) его пределом:

Обычно в приложениях с использованием аппарата математики под предельной себестоимостью понимают именно величину (5.13а).

Например, пусть зависимость издержек производства от объема выпускаемой продукции выражается формулой

Определим средние и предельные издержки при объеме продукции Q = 15 ден. ед.

А) Функция средних издержек на единицу продукции определяется по формуле = C/Q, или в нашем случае

откуда (15) = 40 - 0,03 ∙ 225 = 33,25 ден. ед.

Б) Предельные издержки определяются, согласно (5.13а), по формуле

откуда при Q = 15 получаем С' (15) = 19,75 ден. ед.

Иными словами, при средних издержках на производство единицы продукции в 33,25 ден. ед. дополнительные затраты на производство единицы дополнительной продукции составят 19,75 ден. ед. и не превысят средних издержек.

2. В анализе и прогнозах ценовой политики применяется понятие эластичности спроса. Пусть D = f(Р) — функция спроса от цены товара Р (см. п. 3.1). Тогда под эластичностью спроса понимается процентное изменение спроса при изменении цены товара на один процент:

Как и в предыдущем случае, в случае непрерывной зависимости ΔD от ΔQ удобно перейти к пределу при ΔР 0:

Аналогичное понятие можно ввести и для функции предложения S(P). Напомним, что функция D(P) убывает, а функция S(P) возрастает с ростом цены Р.

Укажем некоторые свойства эластичности. Как следует из формулы (5.14а), ее можно выразить так:

Из равенства (5.14 б) следует, что E(D) обладает свойствами логарифма, а значит,

Заметим, что поскольку функция D(P) убывающая, то D'(P) < 0, а тогда согласно формуле (5.14а) и E(D) < 0. Напротив, поскольку функция предложения возрастающая, то соответствующая эластичность E(S) > 0.

Различают три вида спроса в зависимости от величины |E(D)|:

а) если |E(D)| > 1 (E(D) < -1), то спрос считается эластичным;

б) если |E(D)| = 1 (E(D) = -1), то спрос нейтрален;

в) если |E(D)| < 1 (E(D) > -1), то спрос неэластичный.

Рассмотрим два примера из этой области.

Пример 1. Пусть функция спроса описывается формулой

где D₀ и k — известные величины. Найти, при каких значениях цены Р спрос будет эластичным.

Решение. Согласно формуле (5.14а) составляем выражение для E(D):

Для того чтобы спрос был эластичным (случай а), необходимо, чтобы выполнялось неравенство

Пример 2. Найти изменение выручки с увеличением цены на товар при разных вариантах эластичности спроса.

Решение. Выручка I равна произведению цены Р на товар на величину спроса D:

Найдем производную этой функции:

Теперь проанализируем все варианты эластичности спроса, приведенные выше, с учетом формулы (5.14а).

1) E(D) < -1; тогда, подставляя (5.14а) в это неравенство, получаем, что правая часть уравнения (5.15) отрицательна. Таким образом, при эластичном спросе повышение цены Р ведет к снижению выручки. Напротив, снижение цены на товар увеличивает выручку.

2) E(D) = -1. Из (5.14а) следует, что правая часть (5.15) равна нулю, т.е. при нейтральном спросе изменение цены на товар не влияет на выручку.

3) E(D) > -1. Тогда I'(P) > 0, т.е. при неэластичном спросе повышение цены Р на товар приводит к росту выручки.

Понятие эластичности распространяется и на другие области экономики. Рассмотрим один характерный пример.

Пример 3. Пусть зависимость между себестоимостью продукции С и объемом Q ее производства выражается формулой

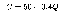
Требуется определить эластичность себестоимости при выпуске продукции Q = 30 ден. ед.

Решение. По формуле (5.14а) получаем

откуда при Q = 30 искомая эластичность составит около —0,32, т.е. при данном объеме выпуска продукции его увеличение на 1% приведет к снижению себестоимости примерно на 0,32%.

Максимизация прибыли

Пусть Q — количество реализованного товара, R(Q) — функция дохода; C(Q) — функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры и т.п. Прибыль от реализации произведенного товара дается формулой

В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Оба упомянутых предельных показателя определяются по аналогии с (5.14а), так что этот принцип можно записать в виде R'(Q) = C'(Q). Действительно, из необходимого условия экстремума для функции (5.16) следует, что П'(Q) = 0, откуда и получается основной принцип.

Пример 4. Найти максимум прибыли, если доход и издержки определяются следующими формулами:

Решение. Согласно (5.16), прибыль П(Q) = - Q³ + 36Q² - 69Q — 4000. Приравнивая производную функции прибыли к нулю, получаем уравнение

Корни этого уравнения Q₁ = 1, Q₂ = 23. Проверка показывает, что максимальная прибыль достигается при Q = 23: П_mах = 1290.

Закон убывающей эффективности производства

Этот закон утверждает, что при увеличении одного из основных факторов производства, например капитальных затрат К, прирост производства начиная с некоторого значения К является убывающей функцией. Иными словами, объем произведенной продукции V как функция от К описывается графиком со сменой выпуклости вниз на выпуклость вверх.

Пример 5. Пусть эта функция дается уравнением

где b и с — известные положительные числа (они определяются прежде всего структурой организации производства), а V_lim — предельно возможный объем выпускаемой продукции. Нетрудно подсчитать, что вторая производная функции (5.17) имеет вид

Критическая точка находится из условия V"(K) = 0, откуда

График функции (5.17) приведен на рис. 5.10. В точке перегиба (5.18) выпуклость графика функции вниз меняется на выпуклость вверх. До этой точки увеличение капитальных затрат приводит к интенсивному росту объема продукции: темп прироста объема продукции (аналог первой производной) возрастает, т.е. V"(K) > 0. При К > К_cr темп прироста объема выпускаемой продукции снижается, т.е. V"(K) < 0, и эффективность увеличения капитальных затрат падает.

Таким образом, в стратегии капиталовложений оказывается очень важным моментом определение критического объема затрат, сверх которого дополнительные затраты будут приводить все к меньшей отдаче при данной структуре организации производства. Зная этот прогноз, можно пытаться совершенствовать и менять структуру организации производства: "улучшать" показатели b, с и V_lim в сторону повышения эффективности капиталовложений.

УПРАЖНЕНИЯ

Найти пределы с использованием правила Лопиталя.

5.1. . 5.2. .

5.3. . 5.4. .

5.5. . 5.6. . 5.7. .

5.8. . 5.9. .

5.10. . 5.11. .

5.12. Разложить по формуле Маклорена функцию f(x) = tg x до члена с x³ включительно.

5.13. Разложить по формуле Маклорена функцию f(x) = e^-x до члена с x² включительно.

Найти пределы с использованием разложений по формуле Маклорена.

5.14. . 5.15. .

5.16. . 5.17. .

Найти интервалы выпуклости и точки перегиба графиков функций.

5.18. . 5.19.

5.20. .

Найти асимптоты графиков функций.

5.21. . 5.22. .

5.23. .

Исследовать и построить графики функций.

5.24. . 5.25. .

5.26. . 5.27. .

5.28. . 5.29. .

5.30. . 5.31.

5.32. . 5.33. .

Решите задачи на наибольшее и наименьшее значения.

5.34. Разложить число 12 на два слагаемых так, чтобы их произведение было наибольшим.

5.35. Определить размеры открытого бассейна с квадратным дном объемом V, при которых на облицовку дна и стен пойдет наименьшее количество материала.

5.36. Даны точки А(0, 3) и В(4, 5). На оси Ох найти точку, сумма расстояний от которой до точек А и В наименьшая.

Решите задачи с экономическим содержанием.

5.37. Зависимость между издержками производства С и объемом продукции Q выражается функцией С = 30Q — 0,08Q³. Определить средние и предельные издержки при объеме продукции: а) Q = 5 ед., б) Q = 10 ед.

5.38. Функции долговременного спроса D и предложения S от цены р на мировом рынке нефти имеют соответственно вид

1) Найти эластичность спроса в точке равновесной цены.

2) Как изменятся равновесная цена и эластичность спроса при уменьшении предложения нефти на рынке на 25%?

5.39. Функции спроса D и предложения S от цены р выражаются соответственно уравнениями

Найти эластичность спроса и предложения при равновесной цене, а также изменение дохода (в процентах) при увеличении цены на 10%.

5.40. Зависимость объема выпуска продукции V от капитальных затрат К определяется функцией V = V₀ ln (4 + K³). Найти интервал изменения К, на котором увеличение капитальных затрат неэффективно.