Ответы к упражнениям
Глава 1
Глава 2
Глава 3
Глава 4
Глава 5
Глава 6
Глава 7
Глава 8
Глава 9
Глава 10
Глава 11
Глава 12
Глава 13
Глава 14
Глава 15
Глава 16
Глава 17
Глава 18
Глава 20
Глава 21
Глава 22
Глава 23
Глава 24
Глава 25
Глава 26
Глава 27
Глава 28
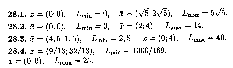
Глава 29
Глава 30
Глава 31
Глава 32
Приложение
Литература
[1] И.Л. Акулич. Математическое программирование в примерах и задачах. М., "Высшая школа", 1986.
[2] В.А. Бабайцев, А.В. Браилов, А.С. Солодовников. Математика в экономике. Часть 5. Руководство к решению задач. Теория вероятностей. М., Финансовая академия при Правительстве РФ, 1999.
[3] М.И. Баканов, А.Д. Шеремет. Теория экономического анализа. — М., "Финансы и статистика", 1994.
[4] Н.П. Башарин. Начала финансовой математики. - М., "ИНФРА-М", 1995.
[5] В.Е. Гмурман. Теория вероятностей и математическая статистика. — М., "Высшая школа", 1998.
[6] В.Е. Гмурман. Руководство по решению задач по теории вероятностей и математической статистике. М., "Высшая школа", 1998.
[7] Н.П. Кондраков. Эккаунтинг для менеджеров. — М., "Дело", 1998.
[8] М.С. Красс. Математика для экономических специальностей. — М., "ИНФРА-М", 1998.
[9] Л.Г. Лабскер, Л.О. Бабешко. Теория массового обслуживания в экономической сфере. — М., "ЮНИТИ", 1998.
[10] А.А. Первозванский, Т.Н. Первозванская. Финансовый рынок: расчет и риск. — М., "ИНФРА-М", 1994.
[11] Г.И. Фалин. Математический анализ рисков в страховании. — М., Российский Юридический Издательский Дом, 1994.
[12] В.В. Федосеев. Экономико-математические модели и методы в маркетинге. - М., "Финстатпром",1996.
[13] В.А. Чернов. Анализ коммерческого риска. — М., "Финансы и статистика", 1998.
[14] Е.М. Четыркин. Методы финансовых и коммерческих расчетов. — М., "ИНФРА-М", 1995.
[15] B.C. Шипачев. Высшая математика. — М., "Высшая школа", 1995.
[16] В. С. Шипачев. Задачи по высшей математике. — М., "Высшая школа".
Содержание
ПРЕДИСЛОВИЕ 3
ВВЕДЕНИЕ 3
Раздел I. ОСНОВЫ МАТЕМАТИКИ 4
Часть 1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ 4
Глава 1. МНОЖЕСТВА 4
1.1. Множества. Основные обозначения. Операции над множествами 4
1.2. Вещественные числа и их свойства 5
1.3. Числовая прямая (числовая ось) и множества на ней 7
1.4. Грани числовых множеств 7
1.5. Абсолютная величина числа 8
Глава 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 8
2.1. Числовые последовательности 9
2.2 Применение в экономике 12
Глава 3. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 14
3.1. Понятие функции 14
3.2. Предел функции 19
3.3. Теоремы о пределах функций 21
3.4. Два замечательных предела 22
3.5. Бесконечно малые и бесконечно большие функции 24
3.6. Понятие непрерывности функции 24
3.7. Непрерывность элементарных функций 25
3.8. Понятие сложной функции 27
3.9. Элементы аналитической геометрии на плоскости 28
Глава 4. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 33
4.1. Понятие производной 33
4.2. Понятие дифференциала функции 35
4.3. Правила дифференцирования суммы, произведения и частного 37
4.4. Таблица производных простейших элементарных функций 37
4.5. Дифференцирование сложной функции 37
4.6. Понятие производной n-го порядка 39
Глава 5. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ В ИССЛЕДОВАНИИ ФУНКЦИЙ 41
5.l. Раскрытие неопределенностей 41
5.2. Формула Маклорена 43
5.3. Исследование функций и построение графиков 45
5.4. Применение в экономике 53
Глава 6. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 59
6.1. Первообразная и неопределенный интеграл 59
6.2. Основные свойства неопределенного интеграла 60
6.3. Таблица основных неопределенных интегралов 60
6.4. Основные методы интегрирования 61
Глава 7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 67
7.1. Условия существования определенного интеграла 67
7.2. Основные свойства определенного интеграла 69
7.3. Основная формула интегрального исчисления 70
7.4. Основные правила интегрирования 72
7.5. Геометрические приложения определенного интеграла 74
7.6. Некоторые приложения в экономике 77
7.7. Несобственные интегралы 79
Глава 8. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 84
8.1. Евклидово пространство Em 84
8.2. Множества точек евклидова пространства Еm 84
8.3. Частные производные функции нескольких переменных 89
8.4. Локальный экстремум функции нескольких переменных 92
8.5. Применение в задачах экономики 94
Часть 2. ЭЛЕМЕНТЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 99
Глава 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 100
9.1. Основные понятия 100
9.2. Уравнения с разделяющимися переменными 102
9.3. Неполные уравнения 104
9.4. Линейные уравнения первого порядка 105
Глава 10. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 108
10.1. Основные понятия теории 108
10.2. Уравнения, допускающие понижение порядка 109
10.3. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами 112
10.4. Краевая задача для дифференциального уравнения второго порядка 115
Глава 11. АППАРАТ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЭКОНОМИКЕ 117
11.1. Дифференциальные уравнения первого порядка 117
11.2. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) 123
Часть 3. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 126
Глава 12. ВЕКТОРЫ 126
12.1. Векторное пространство 126
12.2. Линейная зависимость векторов 128
12.3. Разложение вектора по базису 130
Глава 13. МАТРИЦЫ 133
13.1. Матрицы и операции над ними 133
Понятие матрицы 133
13.2. Обратная матрица 139
Глава 14. ОПРЕДЕЛИТЕЛИ 140
14.1. Операции над определителями и основные свойства 140
14.2. Ранг матрицы и системы векторов 144
Глава 15. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 145
15.1. Основные понятия 145
15.2. Методы решения систем линейных уравнений 147
15.3. Вычисление обратной матрицы методом Гаусса 154
15.4. Геометрическая интерпретация системы линейных уравнений 155
15.5. Однородные системы линейных уравнений 155
Глава 16. ПРИМЕНЕНИЕ ЭЛЕМЕНТОВ ЛИНЕЙНОЙ АЛГЕБРЫ В ЭКОНОМИКЕ 161
16.1. Использование алгебры матриц 161
16.2. Модель Леонтьева многоотраслевой экономики 166
16.3. Линейная модель торговли 170
Часть 4. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 173
Глава 17. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ 173
17.1. Основные понятия теории вероятностей 174
17.2. Теорема сложения вероятностей 176
17.3. Теорема умножения вероятностей 178
17.4. Обобщения теорем сложения и умножения 180
17.5. Схема независимых испытаний 184
Глава 18. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 190
18.1. Случайные величины и законы их распределения 190
18.2. Числовые характеристики дискретных случайных величин 194
18.3. Система двух случайных величин 201
18.4. Непрерывные случайные величины 204
18.5. Основные распределения непрерывных случайных величин 210
18.6. Некоторые элементы математической статистики 215
Раздел II. ОСНОВЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 225
Часть 5. ЭЛЕМЕНТЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 226
Глава 19. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В n-МЕРНОМ ПРОСТРАНСТВЕ 228
19.1. Основные понятия и определения 228
19.2. Решение систем m линейных неравенств с двумя переменными 230
Глава 20. ГРАФИЧЕСКИЙ МЕТОД 233
20.1. Постановка задачи 233
20.2. Алгоритм решения задач 233
20.3. Выбор оптимального варианта выпуска изделий 234
20.4. Экономический анализ задач с использованием графического метода 235
Глава 21. СИМПЛЕКСНЫЙ МЕТОД 240
21.1. Общая постановка задачи 240
21.2. Алгоритм симплексного метода 240
21.3. Анализ эффективности использования производственного потенциала предприятия 242
21.4. Альтернативный оптимум 244
Глава 22. ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ 249
22.2. Основные теоремы двойственности 250
22.3. Решение двойственных задач 252
22.4. Экономический анализ задач с использованием теории двойственности 256
22.5. Стратегическое планирование выпуска изделий с учетом имеющихся ресурсов 258
Глава 23. ТРАНСПОРТНАЯ ЗАДАЧА 262
23.1. Общая постановка задачи 262
23.2. Нахождение исходного опорного решения 264
23.3. Определение эффективного варианта доставки изделий к потребителю 264
23.4. Проверка найденного опорного решения на оптимальность 265
23.5. Переход от одного опорного решения к другому 266
23.6. Альтернативный оптимум в транспортных задачах 268
23.7. Вырожденность в транспортных задачах 271
23.8. Открытая транспортная задача 272
23.9. Определение оптимального варианта перевозки грузов с учетом трансформации спроса и предложений 274
23.10. Экономический анализ транспортных задач 275
23.11. Приложение транспортных моделей к решению некоторых экономических задач 278
23.12. Выбор оптимального варианта использования производственного оборудования 278
Глава 24. ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ 282
24.1. Общая формулировка задачи 282
24.2. Графический метод решения задач 283
24.3. Прогнозирование эффективного использования производственных площадей 283
24.4. Метод Гомори 285
Глава 25. ПАРАМЕТРИЧЕСКОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 288
25.1. Постановка задачи 288
25.2. Линейное программирование с параметром в целевой функции 288
25.3. Определение диапазона оптимального решения выпуска продукции при изменении условий реализации 290
25.4. Транспортная параметрическая задача 293
25.5. Нахождение оптимальных путей транспортировки грузов при нестабильной загрузке дорог 294
Глава 26. ЗАДАЧА О НАЗНАЧЕНИЯХ 300
26.1. Постановка задачи 300
26.2. Алгоритм решения задачи 301
26.3. Планирование загрузки оборудования с учетом максимальной производительности станков 303
26.4. Выбор инвестиционных проектов в условиях ограниченности финансовых ресурсов 304
Глава 27. ЗАДАЧИ С НЕСКОЛЬКИМИ ЦЕЛЕВЫМИ ФУНКЦИЯМИ 306
27.1. Формулировка задачи 307
27.2. Математическая модель нахождения компромиссного решения 307
27.3. Определение оптимального выпуска продукции при многокритериальных экономических показателях 308
Часть 6. ЭЛЕМЕНТЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 310
Глава 28. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 310
28.1. Общая постановка задачи 310
28.2. Графический метод 311
28.3. Дробно-линейное программирование 315
28.4. Метод множителей Лагранжа 321
Глава 29. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ 326
29.1. Постановка задачи 326
29.2. Некоторые экономические задачи, решаемые методами динамического программирования 326
Глава 30. СЕТЕВЫЕ МОДЕЛИ 338
30.1. Основные понятия сетевой модели 339
30.2. Минимизация сети 352
Часть 7. ПРИНЯТИЕ РЕШЕНИЙ И ЭЛЕМЕНТЫ ПЛАНИРОВАНИЯ 360
Глава 31. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИГР 360
31.1. Графическое решение игр вида (2 x n) и (m x 2) 363
31.2. Решение игр (aij)mxn с помощью линейного программирования 368
31.3. Применение матричных игр в маркетинговых исследованиях 370
31.4. Сведение матричной игры к модели линейного программирования 371
31.5. Игры с "природой" 372
31.6. Определение производственной программы предприятия в условиях риска и неопределенности с использованием матричных игр 373
31.7. "Дерево" решений 376